辽宁省丹东市五校2024届九年级上学期12月联考数学试卷(含答案)

这是一份辽宁省丹东市五校2024届九年级上学期12月联考数学试卷(含答案)，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题(每题3分,共30分)
1.一元二次方程x2-3x=0的解是（ ）
A、0 B、3 C、0，3 D、0，-2
2.如图，下列四个几何体中，它们各自的三视图（主视图、左视图、俯视图）不完全相同的几何体是（ ）
A、①②B、②③C、②④D、③④
3.神奇的自然界处处蕴含着数学知识.动物学家在鹦鹉螺外壳上发现,其每圈螺纹的直径与相邻螺纹直径的比约为0.618.这体现了数学中的( )
平移B.旋转C.轴对称D.黄金分割
4.下列命题中，真命题是( )
A．对角线相等的四边形是平行四边形
B．对角线互相垂直平分的四边形是正方形
C．对角线互相垂直的四边形是菱形
D．四个角相等的四边形是矩形
5.如图,DE‖BC,,则 QUOTE , S-?ADE., : S-???DECB.=( )
A．1：2 B．1：3 C．1：4 D．1：5
6. 一元二次方程的根的情况是（ ）
A. 有两个不等的实数根B. 有两个相等的实数根
C. 无实数根D. 无法确定
7.如图，菱形ABCD的周长为24cm，对角线AC、BD相交于O点，
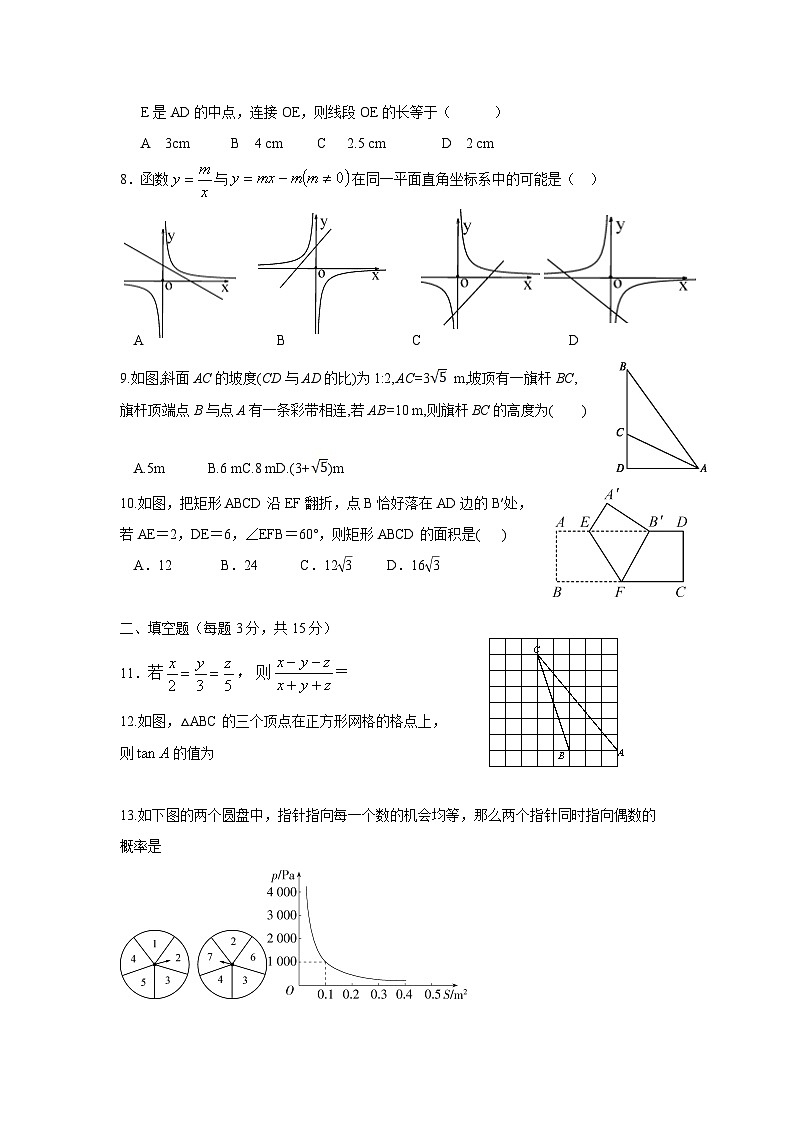
E是AD的中点，连接OE，则线段OE的长等于（ ）
A 3cm B 4 cm C 2.5 cm D 2 cm
8．函数与在同一平面直角坐标系中的可能是（ ）
A B C D
9.如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3 m,坡顶有一旗杆BC,
旗杆顶端点B与点A有一条彩带相连,若AB=10 m,则旗杆BC的高度为( )
A.5m B.6 mC.8 mD.(3+)m
10.如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，
若AE＝2，DE＝6，∠EFB＝60°，则矩形ABCD的面积是( )
A．12 B．24 C．12eq \r(3) D．16eq \r(3)
二、填空题（每题3分，共15分）
11．若 QUOTE ,x-2.=,y-3.=,z-5.，则 QUOTE ,x-y-z-x+y+z.=
12.如图，△ABC的三个顶点在正方形网格的格点上，
则的值为
13.如下图的两个圆盘中，指针指向每一个数的机会均等，那么两个指针同时指向偶数的
概率是
第13题图 第14题图
14.根据物理学知识,在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,其函数图象如上图所示,当S=0.25 m2时,该物体承受的压强p的值为 Pa.
15.如图,在正方形ABCD中,点E是边BC上的一点,点F在边CD的延长线上,且BE=DF,连接EF交边AD于点G.过点A作AN⊥EF,垂足为点M,交边CD于点N.若BE=5,CN=8,则线段AN的长为 .
三、解答题（共75分）
16.（5分）（1）解方程
（5分）（2）计算
17.（8分）某超市销售一种矿泉水，进价为每箱24元，现在的售价为每箱36元，每月可销售60箱.经市场调查发现：若这种矿泉水的售价每降价1元，则每月的销量将增加10箱．如果该超市想要每月销售这种矿泉水的利润为650元，那么每箱矿泉水需要降价多少元？
18.（8分）“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.小文购买了“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张(不放回),再从中随机抽取一张。
（1）请用列表法或画树状图的方法，表示所有可能出现的结果。
（2）求小乐抽到的两张邮票恰好是“立春”和“立夏”的概率。
19.（8分）如图①，在Rt△ABC中，∠ACB＝90°，∠A＝60°，CD是斜边AB上的中线，点E为射线BC上一点，将△BDE沿DE折叠，点B的对应点为点F．
（1）若AB＝a．直接写出CD的长（用含a的代数式表示）；
（2）若DF⊥BC，垂足为G，点F与点D在直线CE的异侧，连接CF，如②，判断四边形ADFC的形状，并说明理由；
20.(8分)某校“综合与实践”活动小组的同学要测量AB,CD两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在AB,CD两楼之间上方的点O处,点O距地面AC的高度为60 m,此时观测到楼AB底部点A处的俯角为70°,楼CD上点E处的俯角为30°,沿水平方向由点O飞行24 m到达点F,测得点E处的俯角为60°,其中点A,B,C,D,E,F,O均在同一竖直平面内.请根据以上数据求楼AB与CD之间的距离AC(结果精确到1 m.参考数据:sin 70°≈0.94,cs 70°≈0.34,tan 70°≈2.75,≈1.73).
21.（9分）
折一折：将正方形纸片ABCD折叠，使边AB、AD都落在对角线AC上，展开得折痕AE、AF，连接EF，如图1．
（1）∠EAF＝ °；
转一转：将图1中的∠EAF绕点A旋转，使它的两边分别交边BC、CD于点P、Q，连接PQ，如图2．
（2）写出线段BP、PQ、DQ之间的数量关系，并说明理由；
（3）连接正方形对角线BD，若图2中的∠PAQ的边AP、AQ分别交对角线BD于点M、点N，如图3，直接写出的值。
22.（12分）（2021•广安）如图，一次函数y1＝kx+b（k≠0）的图象与反比例函数y2＝（m≠0）的图象交于A（-1，n），B（3，-2）两点．
（1）求一次函数和反比例函数的解析式；
（2）直接写出不等式kx+b≥的解集．
（3）点P在x轴上，且满足△ABP的面积等于4，求点P的坐标．
23.（12分）问题情境:在Rt△ABC中,∠BAC=90°,AB=6,AC=8.直角三角板EDF中∠EDF=90°,将三角板的直角顶点D放在Rt△ABC斜边BC的中点处,并将三角板绕点D旋转,三角板的两边DE,DF分别与边AB,AC交于点M,N.
猜想证明:(1)如图①,在三角板旋转过程中,当点M为边AB的中点时,试判断四边形AMDN的形状,并说明理由;
问题解决:(2)如图②,在三角板旋转过程中,当∠B=∠MDB时,求线段CN的长;
(3)如图③,在三角板旋转过程中,当AM=AN时,直接写出线段AN的长.
图①图②
图③
2023年九（上）联考数学试卷答案
选择题
C 2.B 3.D4.D 5.B6.B 7.A 8.C 9.B 10.D
填空题：
12 . 13. 14. 400 15.
解答题：
（1）（5分）方程的解为2和3 （2）（5分）计算结果为 -2
（8分）
解：设每箱降价元，则每月可销售(10+60)箱，依题意得：
(36−x−24)(10x+60)=650，整理得：−10+60x+720=650，
即，∴，解得：(舍去)．
答：每箱矿泉水需要降价7元．
（8分）
画出树状图如图.
可知共有12种等可能的情况 (6分)
(2)其中恰好抽到“立春”和“立夏”的有2种,则所求概率为= (8分)
19.（8分）
解：（1）如图①，在Rt△ABC中，∠ACB＝90°，
∵CD是斜边AB上的中线，AB＝a，
∴CD＝AB＝a． (2分)
（2）四边形ADFC是菱形．
理由如下：
如图②∵DF⊥BC于点G，
∴∠DGB＝∠ACB＝90°，
∴DF∥AC；
由折叠得，DF＝DB，
∵DB＝AB，
∴DF＝AB；
∵∠ACB＝90°，∠A＝60°，
∴∠B＝90°﹣60°＝30°，
∴AC＝AB，
∴DF＝AC，
∴四边形ADFC是平行四边形；
∵AD＝AB，
∴AD＝DF，
∴四边形ADFC是菱形． (8分)
20.（8分）
解析 延长AB和CD分别与直线OF交于点G和点H,(1分)
则∠AGO=∠EHO=90°.
又∵∠GAC=90°,∴四边形ACHG是矩形.
∴GH=AC.(2分)
由题意,得AG=60,OF=24,∠AOG=70°,∠EOF=30°,∠EFH=60°.
在Rt△AGO中,∠AGO=90°,tan∠AOG=,
∴OG==≈≈21.8.(4分)
∵∠EFH是△EOF的外角,
∴∠FEO=∠EFH-∠EOF=60°-30°=30°.
∴∠EOF=∠FEO.∴EF=OF=24.(5分)
在Rt△EHF中,∠EHF=90°,cs∠EFH=,
∴FH=EF·cs∠EFH=24×cs60°=12.(6分)
∴AC=GH=GO+OF+FH=21.8+24+12≈58.(7分)
答:楼AB与CD之间的距离AC约为58m.(8分)
（9分）
（1）解：如图1，答案为：45， (2分)
（2）解：结论：PQ＝BP+DQ．
理由：如图2中，延长CB到T，使得BT＝DQ．
∵AD＝AB，∠ADQ＝∠ABT＝90°，DQ＝BT，
∴△ADQ≌△ABT（SAS），
∴AT＝AQ，∠DAQ＝∠BAT，
∵∠PAQ＝45°，
∴∠PAT＝∠BAP+∠BAT＝∠BAP+∠DAQ＝45°，
∴∠PAT＝∠PAQ＝45°，
∵AP＝AP，
∴△PAT≌△PAQ（SAS），
∴PQ＝PT，
∵PT＝PB+BT＝PB+DQ，
∴PQ＝BP+DQ．
故答案为：PQ＝BP+DQ． (7分)
（3）解：如图3中，
∵四边形ABCD是正方形，
∴∠ABM＝∠ACQ＝∠BAC＝45°，AC＝AB，
∵∠BAC＝∠PAQ＝45°，
∴∠BAM＝∠CAQ，
∴△CAQ∽△BAM，
∴＝＝，
故答案为：． (9分)
（12分）
解：（1）由题意可得：
点B（3，﹣2）在反比例函数图像上，
∴，则m＝﹣6，
∴反比例函数的解析式为，
将A（﹣1，n）代入，
得：，即A（﹣1，6），
将A，B代入一次函数解析式中，得
，解得：，
∴一次函数解析式为y1＝﹣2x+4； (6分)
(8分)
（3）∵点P在x轴上，
设点P的坐标为（a，0），
∵一次函数解析式为y1＝﹣2x+4，令y＝0，则x＝2，
∴直线AB与x轴交于点（2，0），
由△ABP的面积为4，可得：
|a﹣2|＝4，即|a﹣2|＝4，
解得：a＝1或a＝3，
∴点P的坐标为（1，0）或（3，0）． (12分)
（12分）
解析 (1)四边形AMDN为矩形.(1分)
理由如下:∵点M为AB的中点,点D为BC的中点,
∴MD∥AC.(2分)
∴∠AMD+∠A=180°.∵∠A=90°,∴∠AMD=90°.(3分)
∵∠EDF=90°,∴∠A=∠AMD=∠MDN=90°.
∴四边形AMDN为矩形.(4分)
(2)解法一:在Rt△ABC中,∠A=90°,AB=6,AC=8,
∴∠B+∠C=90°,BC==10.
∵点D是BC的中点,∴CD=BC=5.(5分)
∵∠EDF=90°,∴∠MDB+∠1=90°.
∵∠B=∠MDB,∴∠1=∠C.(6分)
∴ND=NC.
过点N作NG⊥BC于点G,则∠CGN=90°.(7分)
∴CG=CD=.(8分)
∵∠C=∠C,∠CGN=∠CAB=90°,
∴△CGN∽△CAB.(9分)
∴=,即=.∴CN=.(10分)
解法二:连接AD.(5分)
在Rt△ABC中,∠BAC=90°,AB=6,AC=8,
∴∠B+∠C=90°,BC==10.
∵点D为BC的中点,∴CD=BC=5.(6分)
同时,AD=BC=CD.∴∠2=∠C.(7分)
∵∠EDF=90°,∴∠MDB+∠1=90°.
∵∠B=∠MDB,∴∠1=∠C.(8分)
∴∠1=∠2.∵∠C=∠C,∴△CDN∽△CAD.(9分)
∴=,即=.∴CN=.(10分)
(3)AN=.(12分)
详解:设AM=AN=x,则BM=6-x,CN=8-x,分别作MP⊥BC于点P,NQ⊥BC于点Q,
∵∠A=∠EDF=90°,AB=6,AC=8,
∴BC==10,sinB=,csB=,
sinC=,csC=,
∴MP=(6-x),BP=(6-x),
NQ=(8-x),CQ=(8-x),
又D为BC的中点,∴DB=CD=5,
∴DP=BD-BP=,DQ=CD-CQ=,
易证△DQN∽△MPD,∴=,
∴=,
化简得175x=625,∴x=.故AN=.