初中数学北师大版九年级下册6 利用三角函数测高教课内容课件ppt

这是一份初中数学北师大版九年级下册6 利用三角函数测高教课内容课件ppt，共25页。PPT课件主要包含了逐点学练，本节小结，作业提升，学习目标，本节要点，学习流程，知识点，感悟新知，测量倾斜角，利用三角函数测高等内容，欢迎下载使用。

测量倾斜角测量底部可以到达的物体的高度测量底部不可以到达的物体的高度
1. 测倾器 测量倾斜角可以用测倾器. 简单的测倾器由度盘、铅锤和支杆组成(如图1-6-1).
特别提醒1. “刻度为90° ~0° ~90°”的意思是使半圆度盘的刻度以0°为中心，然后向左、向右分别增加到90°，即度盘的刻度不是0° ~180°.2.测倾器的原理是对顶角相等及同角的余角相等.3.两点间互看的仰角和俯角的度数是相等的(两直线平行，内错角相等).
2. 使用测倾器测量倾斜角的步骤(1)把支杆竖直插入地面，使支杆的中心线、铅垂线和度盘的0°刻度线重合，这时度盘的顶线PQ 在水平位置.(2)转动度盘，使度盘的直径对准目标，记下此时铅垂线所指的度数.根据对顶角相等及同角的余角相等可以知道，所测倾斜角(即仰角、俯角)于铅垂线所指的度数，读出铅垂线所指的度数，即为倾斜角的度数.
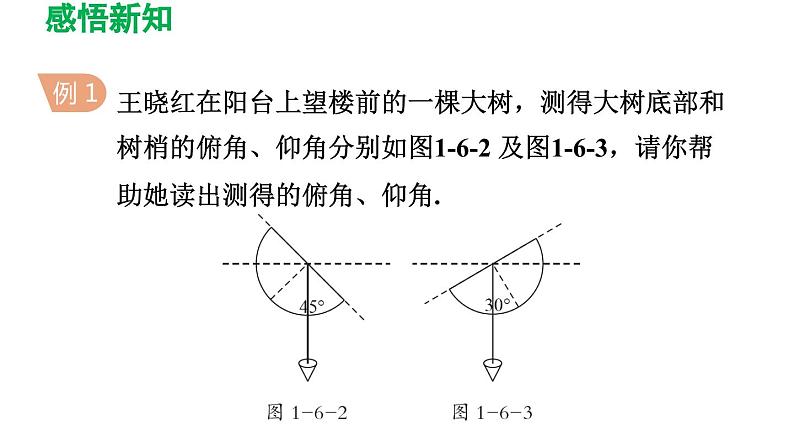
王晓红在阳台上望楼前的一棵大树，测得大树底部和树梢的俯角、仰角分别如图1-6-2 及图1-6-3，请你帮助她读出测得的俯角、仰角.
解题秘方：紧扣测倾器测量倾斜角的步骤，读出俯角和仰角的度数.
解：俯角为45°，仰角为30°.
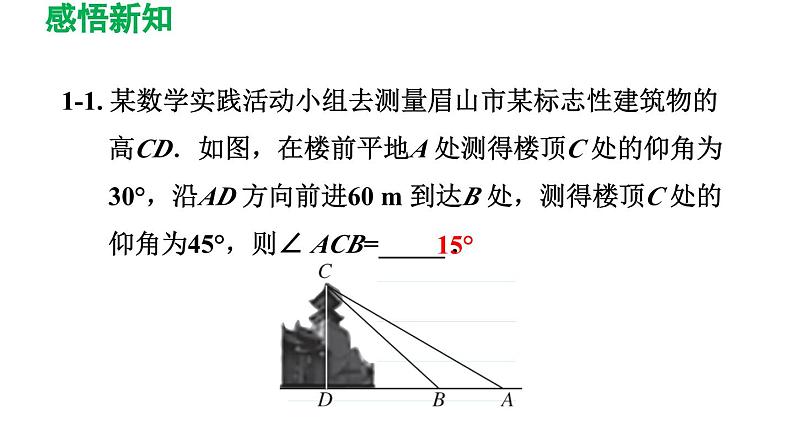
1-1. 某数学实践活动小组去测量眉山市某标志性建筑物的高CD．如图，在楼前平地A 处测得楼顶C 处的仰角为30°，沿AD 方向前进60 m 到达B 处，测得楼顶C 处的仰角为45°，则∠ ACB=_____ .
测量底部可以到达的物体的高度
所谓“底部可以到达”，就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
如图1-6-4，测量MN 高度的步骤如下：(1)在测点A 处安置测倾器，测得M 的仰角∠ MCE=α ；(2)量出测点A 到物体底部N 的水平距离AN=l；(3)量出测倾器的高度AC=a .求出MN 的高度MN=ME+EN=ltanα +a.
特别提醒●测量时，测倾器的支杆必须与水平面垂直，而不是与所在的地面垂直，注意不要忘记测倾器的高度.●为了尽可能减少误差，一般对同一测量对象多次测量取平均值.
如图1-6-5，李亮用测倾器在点D 处测量旗杆BC 的高度，测倾器的高度AD=1.21 m，地面上DC=20.04 m，仰角α=28°，请你帮李亮计算一下旗杆BC 有多高(结果精确到0.1 m，参考数据：sin 28°≈ 0.469 5，cs 28°≈ 0.882 9，tan 28°≈ 0.531 7).
解题秘方：紧扣测倾器测出的角度以及解直角三角形求出高度.
解: 如图1-6-5，过点A 作AE ⊥ BC 于点E，由题意，得AE=DC=20.04 m，EC=AD=1.21 m，∠ BAE=α =28°.在Rt △ ABE 中，BE=AE·tan α =20.04×tan 28°≈20.04×0.531 7≈10.66(m).∴ BC=BE+EC ≈ 10.66+1.21 ≈ 11.9(m).∴旗杆BC 的高约为11.9 m.
2-1. 如图，小明为了测量学校旗杆CD的高度，在地面离旗杆底部C 处24 m 的A 处放置高度为1.5 m 的测角仪AB，测得旗杆顶端D 的仰角为32°，求旗杆CD 的高度.(结果精确到0.1 m，参考数据：sin 32 ° ≈0.53，cs 32°≈ 0.85，tan 32°≈ 0.62)
解：过点B作BE⊥CD于点E，则四边形ABEC为矩形，∴ CE＝AB＝1.5 m，BE＝AC＝24 m. 在Rt△DBE中，∠DBE＝32°，DE＝BE·tan ∠DBE≈24×0.62＝14.88 (m)，∴ CD＝CE＋DE≈1.5＋14.88≈16.4(m)．答：旗杆CD的高度约为16.4 m．
测量底部不可以到达的物体的高度
所谓“底部不可以到达”，就是在地面上不能直接测得测点与被测物体的底部之间的距离.如图1-6-6，测量MN 高度的步骤如下：
(1)在测点A 处安置测倾器，测得此时M 的仰角为∠ MCE=α ；(2)在测点A 与物体之间的B 处安置测倾器，测得此时M 的仰角为∠ MDE=β ；(3)量出测倾器的高度AC=BD=a，以及测点A，B 之间的距离AB=b.借助 =b 求出ME，则MN=ME+EN=
特别提醒1.测量时，测点B必须与A，N在同一条直线上，只有这样才能保证AB+BN=AN成立.2.测量时，测点A与B之间的距离必须可以直接测得.3.两次测量过程中度盘的圆心必须在同一水平面上.
[中考·绍兴] 如图1-6-7，从地面上的点A 看一山坡上的电线杆PQ，测得杆顶端点P 的仰角是45°，向前走6 m 到达点B，测得杆顶端点P 和杆底端点Q 的仰角分别是60°和30°.
解题秘方：解几个直角三角形，根据线段之间的和、差关系求出高度.
(1)求∠ BPQ 的度数；
解：如图1-6-7，延长PQ 交直线AB 于点E.(1)在Rt △ PBE 中，∵∠ PBE=60°，∴∠ BPQ=90°－∠ PBE=90°－60°=30°.
(2)求该电线杆PQ 的高度.(结果精确到1 m，参考数据： ≈ 1.7， ≈ 1 .4 )
解：设PE=x m.在Rt △ APE 中，∠ A=45°，则AE=PE=x m.在Rt △ BPE 中，∠ PEB=90°，∵ tan ∠ PBE = m.∵ AB=AE－BE，
3-1.[2022·重庆南岸区模拟] 如图，山上有一座高塔，山脚下有一圆柱形建筑物平台，高塔及山的剖面与建筑物平台的剖面ABCD 在同一平面内，在点A 处测得塔顶H 的仰角为35°，在D 处测得塔顶H 的仰角为45°
又测得圆柱形建筑物的上底面直径AD为6 m，高CD 为2.8 m，则塔顶端H 到地面的高度HG 约为( )(参考数据：sin35°≈0.57，cs35°≈ 0.82，tan35°≈0.70， ≈1.41)A.10.8 m B.14 mC.16.8 m D.29.8 m