数学选择性必修 第一册2.5 直线与圆、圆与圆的位置多媒体教学课件ppt

这是一份数学选择性必修 第一册2.5 直线与圆、圆与圆的位置多媒体教学课件ppt，共14页。PPT课件主要包含了解几何法，坐标法，思考量小直观简洁，几何法等内容，欢迎下载使用。
1. 能用直线和圆的方程解决一些简单的数学问题与实际问题；2. 会用“坐标法”解决简单直线和圆的方程问题．
情境导学：赵州桥始建于隋代，是一座位于河北省石家庄市赵县城南洨河之上的石拱桥，距今已有 1400 余年的历史. 若已知赵州桥的跨度是 37.4 m，圆拱高约为 7.2 m. 你能求出这座圆拱桥共圆的方程吗？
知识点 1：直线与圆的方程在实际生活中的应用
思考：能用坐标法求解支柱 A2P2 的高度吗？
例 1：如图是某圆拱形桥一孔圆拱的示意图. 圆拱跨度 AB = 20 m，拱高 OP = 4 m，建造时每间隔 4 m 需要用一根支柱支撑，求支柱 A2P2 的高度 (精确到 0.01 m).
求出圆的半 r = 14.5；
① r2 = (r – 4)2 + 102，
求出 |P2A2| = 3.86 m.
② r2 = (|P2A2| + r – 4)2 + 22，
某圆拱形桥一孔圆拱的圆拱跨度 AB = 20 m，拱高 OP = 4 m，建造时每间隔 4 m 需要用一根支柱支撑，求支柱 A2P2 的高度 (精确到 0.01 m).
解：坐标法：以线段 AB 所在直线为 x 轴，线段 AB 的垂直平分线为 y 轴，建立如图所示的直角坐标系；
由题意，点 P、B 的坐标分别为 (0，4)、(10，0)；
设圆心坐标是 (0，b)，半径为r，则圆方程：x2 + (y – b)2 = r2，
把点 P，B 的坐标代入圆的方程 x2 + (y – b)2 = r2 得：b = – 10.5，r2 = 14.52，
所以圆的方程是 x2 + (y + 10.5)2 = 14.52；
把点 P2 的横坐标 x = – 2 代入圆的方程得 y = 3.86 m (已精确到 0.01 m)；
答：支柱 A2P2 的高度约为 3.86 m .
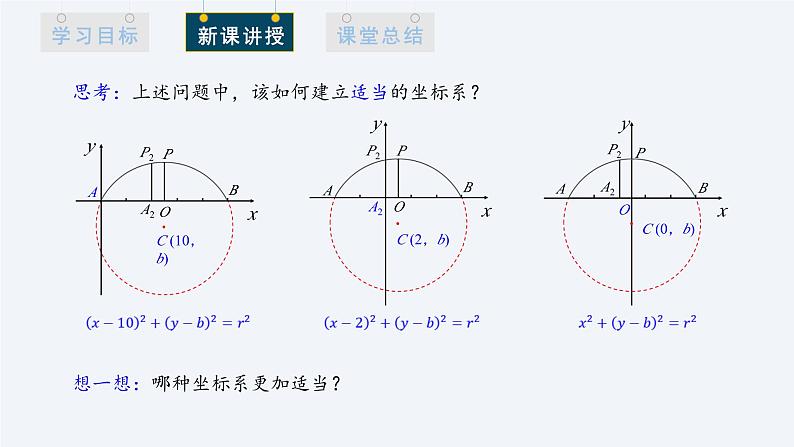
思考：上述问题中，该如何建立适当的坐标系？
想一想：哪种坐标系更加适当？
① 若曲线是轴对称图形，则可选对称轴为坐标轴；② 常选特殊点作为直角坐标系的原点.③ 尽量使已知点位于坐标轴上.
思考：通过上述实例，说说坐标法和几何法各有什么特点？
思考量大，需作辅助线，多次计算
1. 如图，圆弧形桥拱的跨度|AB| = 12 米，拱高|CD| = 4米，则拱桥的直径为(　　)A. 15米 B. 13米 C. 9米 D. 6.5米
例 2：一个小岛的周围有环岛暗礁，暗礁分布在以小岛中心为圆心，半径为 20 km 的圆形区域内. 已知小岛中心位于轮船正西 40 km 处，港口位于小岛中心正北 30 km 处. 如果轮船沿直线返港，那么它是否会有触礁危险？
分析：选择合适的原点建立坐标系，将情境中几何要素用坐标和方程表示，再解答即可；
解：如图，以小岛中心为原点 O，东西方向为 x 轴，南北方向为 y 轴建立直角坐标系，则港口所在位置坐标 (0，3) 船所在位置坐标 (4，0)；所以暗礁所在圆形区域边缘对应圆 O 的方程为：x2 + y2 = 4，圆心坐标 (0，0)，半径为2；轮船航线所在直线 l 方程为：3x + 4y – 12 = 0.
所以直线 l 与圆 O 相离，轮船沿直线返航不会有触礁危险.
① 实际问题 抽象 几何；② 几何 转化 代数 解决代数问题 代数 翻译 几何结论③ 几何 回归 实际问题.
轮船沿直线返航不会有触礁危险.
直线 l 与圆 O 相离
轮船沿直线返港是否有触礁危险？
直线 l 与圆 O 位置关系？
2. 过某圆拱桥的水面跨度 20 m，拱高 4 m. 现有一船，宽 10 m，水面以上高 3 m，则这条船能否从桥下通过.
解：建立如图所示的坐标系，使圆心 C 在 y 轴上，
设这座圆拱桥的拱圆的方程是 (x – a)2 + (y – b)2 = r2，
依题意有 A (-10，0)，B (10，0)，P (0，4)，E (5，0).
将点 A，B，P 代入方程得：a = 0，b = – 10.5，r = 14.5；
将点 F 横坐标代入方程得：y ≈ 3.1 m > 3 m，所以船能通过.
故圆拱桥拱圆的方程是 x2 + (y + 10.5)2 = 14.52 (0 ≤ y ≤ 4)，