初中数学北师大版八年级上册5 三角形的内角和定理达标测试

这是一份初中数学北师大版八年级上册5 三角形的内角和定理达标测试，共16页。

知识点1 三角形内角和定理
1.(2021广西梧州中考)在△ABC中,∠A=20°,∠B=4∠C,则∠C等于( )
A.32° B.36° C.40° D.128°
2.(2023福建顺昌月考)如图,△ABC中,∠A=70°,将△ABC沿DE折叠,点A落在点F处,则∠FDB+∠FEC=()( )
A.140° B.60° C.70° D.80°
3.【新独家原创】如图,在△ABC中,将△BFE沿EF折叠,点B恰好落在点A处,若∠B=36°,∠CAE=30°,则∠C= °.
4.(2023广东广州海珠期末)如图,在△ABC中,AD是高,AE、BF是角平分线,AE与BF交于点O,∠C=70°.
(1)∠AOB的度数为 ;
(2)若∠ABC=60°,求∠DAE的度数.
知识点2 三角形内角和定理的推论
5.(2023湖北利川期末)如图所示,在△ABC中,CD,BE分别是AB,AC边上的高,并且CD,BE交于点P,若∠A=50°,则∠BPC等于()( )
A.130° B.120° C.110° D.100°
6.【教材变式·P182例题】如图,D是△ABC的边AC上一点,E为BD上一点,则∠A,∠1,∠2之间的关系正确的是( )
A.∠A>∠1>∠2 B.∠2>∠1>∠A
C.∠1>∠2>∠A D.无法确定
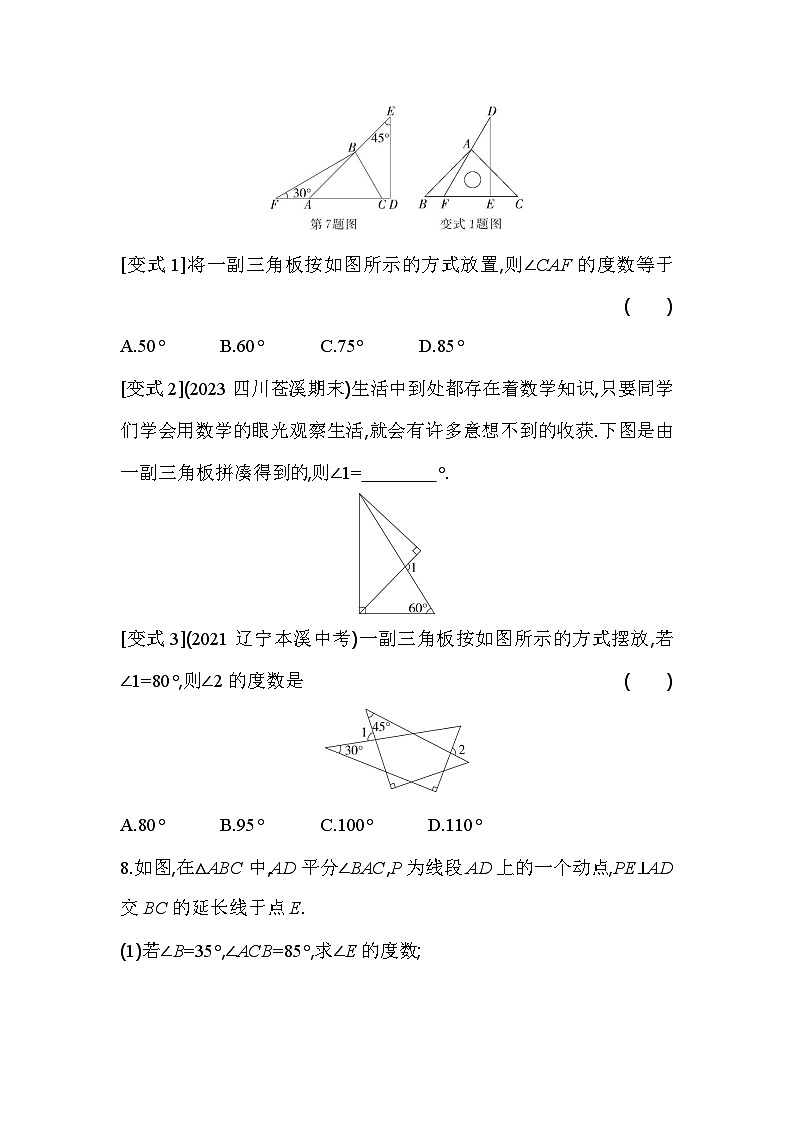
7.【一题多变】(2023湖北武汉武昌校级期中)下图是由一副三角板拼凑得到的,则∠ABC的度数为 ( )
A.50° B.60° C.75° D.80°

[变式1]将一副三角板按如图所示的方式放置,则∠CAF的度数等于( )
A.50° B.60° C.75° D.85°
[变式2](2023四川苍溪期末)生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获.下图是由一副三角板拼凑得到的,则∠1= °.
[变式3](2021辽宁本溪中考)一副三角板按如图所示的方式摆放,若∠1=80°,则∠2的度数是( )
A.80° B.95° C.100° D.110°
8.如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.
(1)若∠B=35°,∠ACB=85°,求∠E的度数;
(2)当P点在线段AD上运动时,猜想∠E与∠B,∠ACB的数量关系,并证明.
能力提升全练
9.(2022山东淄博中考,5,★☆☆)某城市几条道路的位置关系如图所示,道路AB∥CD,道路AB与AE的夹角∠BAE=50°.城市规划部门想新修一条道路CE,要求CF=EF,则∠E的度数为( )
A.23° B.25° C.27° D.30°

10.(2021河北中考,18,★★☆)可调躺椅示意图(数据如图)如图所示,AE与BD的交点为C,且∠CAB,∠CBA,∠E保持不变.为了舒适,需调整∠D的大小,使∠EFD=110°,则图中∠D应 (填“增加”或“减少”) °.
11.(2022贵州黔西南州中考,13,★★☆)如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,∠B=60°,∠D=45°,AC与DE相交于点F.若BC∥AE,则∠AFE的度数为 .()
12.(2022辽宁沈阳铁西期末,21,★★☆)如图,在△ABC中,∠BAC=90°,AB=AC,射线AE交BC于点P,∠BAE=15°.过点C作CD⊥AE于点D,连接BE,过点E作EF∥BC交DC的延长线于点F.
(1)求∠F的度数;
(2)若∠ABE=75°,求证:BE∥CF.
素养探究全练
13.【推理能力】(2023辽宁鞍山期中)在△ABC中,∠C=80°,点D、E分别是△ABC的边AC、BC上的点,点P是一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在边AB上,且∠α=50°,如图1,则∠1+∠2= ;
(2)若点P在边AB上运动,如图2所示,则∠α、∠1、∠2之间的关系为 ;
(3)若点P运动到边AB的延长线上,如图3,则∠α、∠1、∠2之间有何关系?猜想并说明理由.

14.【推理能力】在△ABC中,∠ACB>∠ABC,D,E分别是边BC和BC延长线上的点,连接AD,AE,∠CAE=∠B.
(1)如图1,若∠ADE=60°,∠CAE=40°,求∠BAD的度数;
(2)如图2,已知∠DAE=∠ADE.
①判断AD是否平分∠BAC,并说明理由;
②F为射线AD上一点(不与点D重合),过点F作FG⊥BC,垂足为G.若∠B=α,∠ACB=β,直接用含α,β的式子表示出∠AFG的度数.

答案全解全析
基础过关全练
1.A ∵∠A=20°,∠B=4∠C,且∠A+∠B+∠C=180°,
∴20°+4∠C+∠C=180°,
∴5∠C=160°,
∴∠C=32°.
故选A.
2.A ∵△DEF是由△DEA折叠而成的,
∴∠F=∠A=70°,∠A+∠ADF+∠AEF+∠F=360°,
∴∠ADF+∠AEF=360°-∠A-∠F=220°,
∵∠FDB=180°-∠ADF,∠FEC=180°-∠AEF,
∴∠FDB+∠FEC=360°-(∠ADF+∠AEF)=140°,故选A.
3.78
解析 ∵将△BFE沿EF折叠,点B恰好落在点A处,
∴∠EAF=∠B=36°,
∵∠CAE=30°,
∴∠BAC=∠EAF+∠CAE=66°,
∴∠C=180°-∠B-∠BAC=180°-36°-66°=78°.
4.解析 (1)∵AE、BF是∠BAC、∠ABC的平分线,
∴∠OAB+∠OBA=12(∠BAC+∠ABC),
在△ABC中,∠C=70°,
∴∠BAC+∠ABC=180°-∠C=110°,
∴∠AOB=180°-∠OAB-∠OBA=180°-12(∠BAC+∠ABC)=125°.
(2)∵在△ABC中,AD是高,∠C=70°,∠ABC=60°,∴∠DAC=90°-∠C=90°-70°=20°,∠BAC=180°-∠ABC-∠C=50°,
∵AE是∠BAC的平分线,
∴∠CAE=12∠BAC=25°,
∴∠DAE=∠CAE-∠CAD=25°-20°=5°,
∴∠DAE的度数为5°.
5.A ∵∠A=50°,BE⊥AC,
∴∠ABE=90°-50°=40°,
又∵CD⊥AB,
∴∠BDP=90°,
∴∠BPC=∠BDP+∠ABE=130°.
故选A.
6.B ∵∠2=∠1+∠DCE,∠1=∠A+∠ABD,
∴∠2>∠1>∠A.
故选B.
7.C ∵∠F=30°,∠BAC=45°,∠BAC是△ABF的外角,∴∠ABF=∠BAC-∠F=15°,
∵∠CBF=90°,
∴∠ABC=∠CBF-∠ABF=75°.
故选C.
[变式1] C ∵∠DAC=∠DFE+∠C=60°+45°=105°,∴∠CAF=180°-∠DAC=75°.
[变式2] 105
解析 如图,∵∠CAB=90°,∠CAD=45°,
∴∠EAB=45°,
∵∠1是△ABE的一个外角,
∴∠1=∠EAB+∠ABC=45°+60°=105°.
[变式3] B 如图,∠3=∠1-45°=35°,
∴∠4=∠3=35°,
∴∠2=∠4+∠5=95°,故选B.
8.解析 (1)∵∠B=35°,∠ACB=85°,
∴∠BAC=60°,
∵AD平分∠BAC,
∴∠BAD=∠DAC=30°,
∴∠ADC=30°+35°=65°,
∴∠E=90°-65°=25°.
(2)∠E=12(∠ACB-∠B).
证明:设∠B=n°,∠ACB=m°,
如图,∵AD平分∠BAC,
∴∠1=∠2=12∠BAC,
∵∠B+∠ACB+∠BAC=180°,∠B=n°,∠ACB=m°,
∴∠CAB=(180-n-m)°,
∴∠1=12(180-n-m)°,
∴∠3=∠B+∠1=n°+12(180-n-m)°=90°+12n°-12m°,
∵PE⊥AD,
∴∠DPE=90°,
∴∠E=90°-90°+12n°-12m°=12(m-n)°=12(∠ACB-∠B).
能力提升全练
9.B ∵AB∥CD,∠BAE=50°,
∴∠DFE=∠BAE=50°,
∵CF=EF,
∴∠C=∠E,
∵∠DFE=∠C+∠E=50°,
∴∠E=25°.
故选B.
10.减少;10
解析 如图,延长EF交CD于点G,
∵∠ACB=180°-50°-60°=70°,
∴∠ECD=∠ACB=70°.
∵∠DGF=∠DCE+∠E,
∴∠DGF=70°+30°=100°.
∵∠EFD=110°,∠EFD=∠DGF+∠D,
∴∠D=10°.
∴∠D应减少10°.
故答案为减少;10.
11.105°
解析 在△ABC中,∠BAC=90°,∠B=60°,
∴∠C=180°-∠BAC-∠B=180°-90°-60°=30°,
∵BC∥AE,
∴∠CAE=∠C=30°,
在△ADE中,∠DAE=90°,∠D=45°,
∴∠E=180°-∠DAE-∠D=45°,
∴在△AEF中,∠AFE=180°-∠E-∠CAE=105°.
12.解析 (1)∵∠BAC=90°,∠BAE=15°,AB=AC,
∴∠PAC=75°,∠ABC=∠ACB=45°,
∵CD⊥AE,∴∠ADC=90°,
∴∠ACD=180°-∠ADC-∠DAC=15°,
∴∠PCD=∠PCA-∠ACD=45°-15°=30°,
∵EF∥BC,
∴∠F=∠DCP=30°.
(2)证明:∵∠ABE=75°,∠ABC=45°,
∴∠CBE=75°-45°=30°,
由(1)可得∠DCP=30°,
∴∠DCB=∠CBE,
∴BE∥CF(内错角相等,两直线平行).
素养探究全练
13.解析 (1)如图1,连接CP,
∵∠1是△CDP的外角,
∴∠1=∠DCP+∠DPC,
同理可得,∠2=∠ECP+∠EPC,
∴∠1+∠2=∠ACB+∠DPE=80°+50°=130°.
(2)如图2,连接CP,
∵∠1是△CDP的外角,
∴∠1=∠DCP+∠DPC,
同理可得,∠2=∠ECP+∠EPC,
∴∠1+∠2=∠ACB+∠DPE=80°+∠α.
(3)∠1=80°+∠2+∠α,理由如下:
如图3,设BC与DP交于点M.∵在△CDM中,∠1=∠C+∠CMD,
在△EMP中,∠CMD=∠2+∠α,
∴∠1=∠C+∠2+∠α,
即∠1=80°+∠2+∠α.
14.解析 (1)∵∠CAE=∠B,∠CAE=40°,
∴∠B=40°,
∵∠ADE=∠B+∠BAD,
∴∠BAD=∠ADE-∠B=60°-40°=20°.
(2)①AD平分∠BAC,理由如下:
∵∠DAE=∠ADE,且∠DAE=∠DAC+∠CAE,∠ADE=∠B+∠BAD,
∴∠DAC+∠CAE=∠B+∠BAD,
∵∠CAE=∠B,
∴∠DAC=∠BAD,
∴AD平分∠BAC.
②∠AFG=12(β-α).
详解:如图所示:
∵∠B=α,∠ACB=β,
∴∠BAC=180°-∠B-∠ACB=180°-α-β,
由(2)①知AD平分∠BAC,
∴∠CAD=12∠BAC=12(180°-α-β)=90°-12α-12β,
∴∠ADC=180°-∠CAD-∠ACD=180°-90°-12α-12β-β=90°+12α-12β,
∵∠FDG=∠ADC,
∴∠FDG=90°+12α-12β,
∵FG⊥BC,
∴∠FGD=90°,
∴∠AFG+∠FDG=90°,
∴∠AFG=90°-∠FDG=90°-90°+12α-12β=12(β-α).