吉林省长春市榆树市2022-2023学年七年级下学期6月月考数学试题

这是一份吉林省长春市榆树市2022-2023学年七年级下学期6月月考数学试题，共7页。试卷主要包含了化简等内容，欢迎下载使用。
1．（3分）已知关于x的方程2x﹣a﹣5＝0的解是x＝﹣2，则a的值为（ ）
A．1B．﹣1C．9D．﹣9
2．（3分）把不等式2x﹣1＞﹣5的解集在数轴上表示，正确的是（ ）
A． B．
C． D．
3．（3分）下列图形中，是轴对称图形的是（ ）
A．B．C．D．
4．（3分）已知方程组：，则x+2y的值为（ ）
A．2B．1C．﹣2D．3
5．（3分）用下列一种正多边形铺地板，能恰好铺满地面的是（ ）
A．正五边形B．正六边形C．正七边形D．正八边形
6．（3分）如图，将△ABC沿射线BC方向平移3cm，得到△DEF，点E落在线段BC上．若△ABC的周长为10cm，则四边形ABFD的周长为（ ）
A．20cmB．13cmC．16cmD．24cm
7．（3分）如图，D是△ABC的BC边上一点，∠B＝∠1，∠3＝80°，∠BAC＝70°．则∠2的大小是（ ）
A．20°B．25°C．30°D．35°
8．（3分）如图，六边形ABCDEF内部有一点G，连接BG、DG．若∠1+∠2+∠3+∠4+∠5＝440°，则∠BGD的大小为（ ）
A．60°B．70°C．80°D．90°
二、填空题（每题3分共18分）
9．（3分）化简：＝ ．
10．（3分）已知二元一次方程3x﹣y＝5，用含x的代数式表示y，则y＝ ．
11．（3分）公元前1700年的古埃及纸草书中，记载着一个数学问题：“它的全部，加上它的七分之一，其和等于19．”此问题中“它”的值为 ．
12．（3分）若关于x的不等式组有且只有4个整数解，则k的取值范围是 ．
13．（3分）如图，△ABC≌△DEB，点E在边AB上，DE与AC相交于点F，若∠D＝35°，∠C＝60°，
则∠AFD的大小为 度．
14．（3分）如图，是△ABC中，点D为边BC上任意一点（点D不与点B、点C重合），点E、F分别是线段AD、CE的中点，连结BE、BF．若△ABC的面积为8，则△BEF的面积为 ．
三、解答题（共78分）
15．（6分）解方程组：．
16．（6分）解一元一次不等式：．
17．（6分）图①、图②、图③均是8×8的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，点A、B、C均为格点．只用无刻度的直尺，分别在给定的网格中按下列要求作图，并保留必要的画图痕迹．
（1）在图①中画出△ABC关于直线l对称的图形．
（2）在图②中画出△ABC关于点O成中心对称的图形．
（3）在图③中，过点C画AB的垂线．
18．（6分）解不等式组：并将解集在数轴上表示．
19．（8分）自动驾驶汽车是一种通过电脑系统实现无人驾驶的智能汽车，某出租车公司拟在今明两年共投资6000万元改造220辆无人驾驶出租车投放市场．今年每辆无人驾驶出租车的改造费用是30万元，预计明年每辆无人驾驶出租车的改造费用可下降40%．
（1）求明年每辆无人驾驶出租车的改造费用．
（2）求今年改造的无人驾驶出租车的数量．
20．（8分）如图，△ABC沿着BC的方向平移至△DEF，∠B＝60°，∠F＝40°．
（1）求∠EDF的度数；
（2）若△ABC的周长为15，平移距离为2．则四边形ABFD的周长为 ．
21．（10分）探究：如图①，在△ABC中，∠ACB＝90°，CD⊥AB于点D．若∠B＝30°，则∠ACD的度数是 ．
拓展：如图②，∠MCN＝90°，射线CP在人MCN的内部，点A、B分别在CM、CN上，分别过点A、B作AD⊥CP、BE⊥CP于点D、E．若∠CBE＝70°，求∠CAD的度数．
应用：如图③，点A、B分别在∠MCN的边CM、CN上，射线CP在∠MCN的内部，点D、E在射线CP上，连结AD、BE．若∠MCN＝∠ADP＝∠BEP＝60°，则∠CAD+∠CBE+∠ACB＝ ．
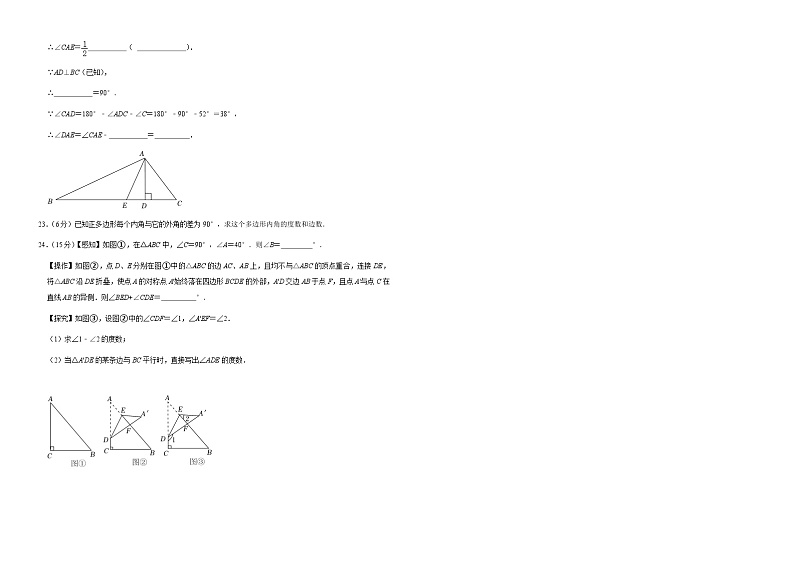
22．（7分）如图，在△ABC中，AD⊥BC于D，AE平分∠BAC交BC于点E，∠B＝28°，∠C＝52°，求∠DAE的度数．
请完善解答过程，并在括号内填写相应的理论依据．
解：∵∠BAC+∠B+∠C＝180°（ ），
∴∠BAC＝180﹣52°﹣28°＝ （等式的性质）．
∵AE平分∠BAC（已知），
∴∠CAE＝ （ ）．
∵AD⊥BC（已知），
∴ ＝90°．
∵∠CAD＝180°﹣∠ADC﹣∠C＝180°﹣90°﹣52°＝38°，
∴∠DAE＝∠CAE﹣ ＝ ．
23．（6分）已知正多边形每个内角与它的外角的差为90°，求这个多边形内角的度数和边数．
24．（15分）【感知】如图①，在△ABC中，∠C＝90°，∠A＝40°．则∠B＝ °．
【操作】如图②，点D、E分别在图①中的△ABC的边AC、AB上，且均不与△ABC的顶点重合，连接DE，将△ABC沿DE折叠，使点A的对称点A'始终落在四边形BCDE的外部，A'D交边AB于点F，且点A'与点C在直线AB的异侧．则∠BED+∠CDE＝ °．
【探究】如图③，设图②中的∠CDF＝∠1，∠A'EF＝∠2．
（1）求∠1﹣∠2的度数；
（2）当△A'DE的某条边与BC平行时，直接写出∠ADE的度数．
七年级数学试题
参考答案
一．选择题（每题3分共24分）
1． D．2． C．3． C．4． A．5． B．6． C．7． C．8． C．
二、填空题（每题3分共18分）
9． 3． 10． 3x﹣5． 11． ． 12．﹣4≤k＜﹣2． 13． 130． 14． 2．
三、解答题（共78分）
15．
解：
①×2得：2x+2y＝6③，
③+②得：5x＝10，
解得x＝2，
把x＝2代入①得：2+y＝3，
解得y＝1，
∴方程组的解是．
16．
解：去分母得：2（x﹣5）+6≤9x，
去括号得：2x﹣10+6≤9x，
移项得：2x﹣9x≤10﹣6，
合并得：﹣7x≤4，
系数化为1得：x≥﹣．
17．
解：（1）如图，△A1B1C1即为所求．
（2）如图，△A2B2C2即为所求．
.
（3）如图，CD即为所求．
18．
解：，
由①得x≤2．
由②得x＞﹣4．
所以原不等式组的解集为﹣4＜x≤2．
解集在数轴上表示：
19．
解：（1）30×（1﹣40%）＝18（万元）．
故明年每辆无人驾驶出租车的预计改装费用是18万元；
（2）设今年改装的无人驾驶出租车是x辆，则明年改装的无人驾驶出租车是（220﹣x）辆，依题意有
30x+18（220﹣x）＝6000，
解得：x＝170．
答：今年改造的无人驾驶出租车是170辆．
20．
解：（1）∵∠F＝40°，AC∥DF，
∴∠ACB＝40°，
∴∠BAC＝180°﹣∠ABC﹣∠ACB＝180°﹣60°﹣40°＝80°，
∵△ABC沿着BC的方向平移至△DEF，
∴∠EDF＝∠ABAC＝80°．
（2）∵AD＝2，
∴CF＝AD＝2，
∴四边形ABFD的周长＝AB+BC+CF+DF+AD，
＝AB+BC+CF+AC+AD，
＝△ABC的周长+AD+CF，
＝15+2+2，
＝19．
故答案为：19．
21．
解：（1）在△ABC中，∠ACB＝90°，∠B＝30°，
∴∠A＝60°，
∵CD⊥AB，
∴∠ADC＝90°，
∴∠ACD＝90°﹣∠A＝30°；
故答案为：30°；
（2）∵BE⊥CP，
∴∠BEC＝90°，
∵∠CBE＝70°，
∴∠BCE＝90°﹣∠CBE＝20°，
∵∠ACB＝90°，
∴∠ACD＝90°﹣∠BCE＝70°，
∵AD⊥CP，
∴∠CAD＝90°﹣∠ACD＝20°；
（3）∵∠ADP是△ACD的外角，
∴∠ADP＝∠ACD+∠CAD＝60°，
同理，∠BEP＝∠BCE+∠CBE＝60°，
∴∠CAD+∠CBE+∠ACB＝∠CAD+∠CBE+∠ACD+∠BCE＝（∠CAD+∠ACD）+（∠CBE+∠BCE）＝120°，
故答案为：120°．
22．
解：∵∠BAC+∠B+∠C＝180°（三角形内角和定理），
∴∠BAC＝180°﹣52°﹣28°＝100°（等式的性质），
∵AE平分∠BAC（已知），
∴∠CAE＝∠BAC（角平分线的定义），
∵AD⊥BC（已知），
∴∠ADC＝90°，
∵∠CAD＝180°﹣∠ADC﹣∠C＝180°﹣90°﹣52°＝38°，
∴∠DAE＝∠CAE﹣∠CAD＝12°．
故答案为：三角形内角和定理，100°，∠BAC，角平分线的定义，∠ADC，∠CAD，12°．
23．
解：设外角是x，则内角是180°﹣x，依题意有
180°﹣x＝x+90°，
解得x＝45°，
180°﹣x＝135°，
而任何多边形的外角是360°，
则多边形中外角的个数是360÷45＝8，
故这个多边形的边数是8，每个内角的度数是135°．
24．∵在△ABC中，∠C＝90°，∠A＝40°，
则∠B＝180°﹣90°﹣40°＝50°，
故答案为：50；
∵在四边形BCDE中，∠C＝90°，∠B＝50°，
∴∠BED+∠CDE＝360°﹣∠C﹣∠B＝360°﹣90°﹣50°＝220°，
故答案为：220；
（1）由折叠，得∠A'＝∠A＝40°．
∵∠A'+∠2+∠A'FE＝180°，
∴∠2＝180°﹣∠A'﹣∠A'FE＝140°﹣∠A'FE，
∵∠B＝50°，∠1+∠C+∠B+∠BFE＝360°，
∴∠1＝360°﹣∠C﹣∠B﹣∠BFD＝220°﹣∠BFD，
∵∠BFD＝∠A'FE，
∴∠1﹣∠2＝220°﹣140°＝80°；
（2）当EA'∥BC时，∠2＝∠B＝50°，
∵∠1﹣∠2＝80°，
∴∠1＝80°+∠2＝80°+50°＝130°，
由折叠性质可得∠ADE＝∠A'DE＝＝25°；
当DA'∥BC时，∠1＝∠C＝90°，
∠ADE＝∠A'DE＝＝45°；
当DE∥BC时，不符合题意，
综上所述：∠ADE的大小为45°或25°．