云南省昆明市呈贡区2023-2024学年九年级数学第一学期期末达标测试试题含答案

这是一份云南省昆明市呈贡区2023-2024学年九年级数学第一学期期末达标测试试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁，校园内有一个由两个全等的六边形，对于抛物线，下列说法正确的是等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。
4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．如图，在菱形ABOC中，∠A=60°，它的一个顶点C在反比例函数的图像上，若菱形的边长为4，则k值为( )
A．B．C．D．
2．下列说法正确的是（ ）
A．打开电视机，正在播放广告是必然事件
B．天气预报明天下雨的概率为％，说明明天一定会下雨
C．买一张体育彩票会中奖是可能事件
D．长度分别为3，5，9厘米的三条线段不能围成一个三角形是随机事件
3．方程 x2＝4的解是（ ）
A．x1＝x2＝2B．x1＝x2＝－2C．x1＝2，x2＝－2D．x1＝4，x2＝－4
4．如图，已知在△ABC中，P为AB上一点，连接CP，以下条件中不能判定△ACP∽△ABC的是（ ）
A．B．C．D．
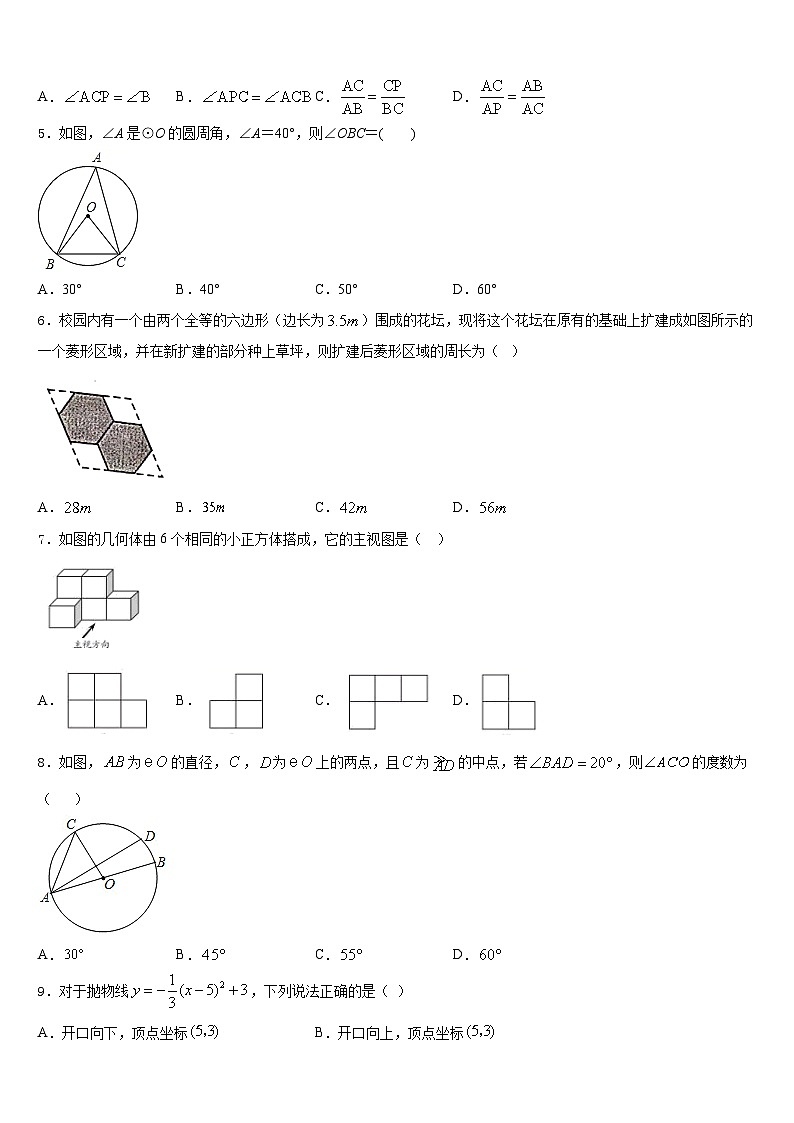
5．如图，∠A是⊙O的圆周角，∠A＝40°，则∠OBC＝( )
A．30°B．40°C．50°D．60°
6．校园内有一个由两个全等的六边形（边长为）围成的花坛，现将这个花坛在原有的基础上扩建成如图所示的一个菱形区域，并在新扩建的部分种上草坪，则扩建后菱形区域的周长为（ ）
A．B．C．D．
7．如图的几何体由6个相同的小正方体搭成，它的主视图是（ ）
A．B．C．D．
8．如图，为的直径，，为上的两点，且为的中点，若，则的度数为（ ）
A．B．C．D．
9．对于抛物线，下列说法正确的是（ ）
A．开口向下，顶点坐标B．开口向上，顶点坐标
C．开口向下，顶点坐标D．开口向上，顶点坐标
10．若抛物线y＝x2+bx+c与x轴只有一个公共点，且过点A（m，n），B（m+8，n），则n＝（ ）
A．0B．3C．16D．9
二、填空题(每小题3分,共24分)
11．已知点 A（a，1）与点 B（﹣3，b）关于原点对称，则 ab 的值为_____．
12．对于实数a，b，定义运算“※”如下：a※b=a2﹣ab，例如，5※3=52﹣5×3=1．若（x+1）※（x﹣2）=6，则x的值为_____．
13．菱形的两条对角线分别是，，则菱形的边长为________，面积为________．
14．从一副扑克牌中取出两张红桃和两张黑桃，将这四张扑克牌洗匀后背面朝上，从中随机摸出两张牌，那么摸到两张都是红牌的概率是__________．
15．为了估计虾塘里海虾的数目，第一次捕捞了500只虾，将这些虾一一做上标记后放回虾塘．几天后，第二次捕捞了2000只虾，发现其中有20只虾身上有标记，则可估计该虾塘里约有_____只虾．
16．如图，△ABC中，DE∥FG∥BC，AD∶DF∶FB＝2∶3∶4，若EG＝4，则AC＝________.
17．对于为零的两个实数a，b，如果规定：a☆b＝ab-b-1，那么x☆（2☆x）=0中x值为____．
18．已知∽，若周长比为4：9，则_____________．
三、解答题(共66分)
19．（10分）如图，某建筑物AC顶部有一旗杆AB，且点A，B，C在同一条直线上，小明在地面D处观测旗杆顶端B的仰角为30°，然后他正对建筑物的方向前进了20米到达地面的E处，又测得旗杆顶端B的仰角为60°，已知建筑物的高度AC=12m，求旗杆AB的高度．
20．（6分）（1）如图①，在△ABC中，AB＝m，AC＝n（n＞m），点P在边AC上．当AP＝ 时，△APB∽△ABC；
（2）如图②，已知△DEF（DE＞DF），请用直尺和圆规在直线DF上求作一点Q，使DE是线段DF和DQ的比例项．（保留作图痕迹，不写作法）
21．（6分）如图，一农户要建一个矩形猪舍，猪舍的一边利用长为15m的住房墙，另外三边用27m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形猪舍的长，宽分别为多少米时，猪舍面积为96m2？
22．（8分）如图，△ABC中，点E在BC边上，AE＝AB，将线段AC绕A点逆时针旋转到AF的位置，使得∠CAF＝∠BAE，连接EF，EF与AC交于点G．求证：EF＝BC．
23．（8分）码头工人每天往一艘轮船上装载货物，装载速度（吨/天）与装完货物所需时间（天）之间的函数关系如图．
（1）求与之间的函数表达式，并写出自变量的取值范围；
（2）由于遇到紧急情况，要求船上的货物不超过5天卸货完毕，那么平均每天至少要卸多少吨货物？
24．（8分）数学兴趣小组到黄河风景名胜区测量炎帝塑像（塑像中高者）的高度．如图所示，炎帝塑像DE在高55m的小山EC上，在A处测得塑像底部E的仰角为34°，再沿AC方向前进21m到达B处，测得塑像顶部D的仰角为60°，求炎帝塑像DE的高度．（精确到1m．参考数据：，，，）
25．（10分）某商店销售一种商品，经市场调查发现：该商品的月销售量y（件）是售价x（元/件）的一次函数，其售价x、月销售量y、月销售利润w（元）的部分对应值如下表：
注：月销售利润＝月销售量×（售价－进价）
（1）①求y关于x的函数表达式；
②当该商品的售价是多少元时，月销售利润最大？并求出最大利润；
（2）由于某种原因，该商品进价提高了m元/件（m＞0），物价部门规定该商品售价不得超过40元/件，该商店在今后的销售中，月销售量与售价仍然满足（1）中的函数关系．若月销售最大利润是2400元，则m的值为 ．
26．（10分）某童装店购进一批20元/件的童装，由销售经验知，每天的销售量y（件）与销售单价x（元）之间存在如图的一次函数关系．
（1）求y与x之间的函数关系；
（2）当销售单价定为多少时，每天可获得最大利润，最大利润是多少？
参考答案
一、选择题(每小题3分,共30分)
1、C
2、C
3、C
4、C
5、C
6、C
7、A
8、C
9、A
10、C
二、填空题(每小题3分,共24分)
11、-2
12、2
13、
14、
15、1．
16、12
17、0或2
18、4：1
三、解答题(共66分)
19、旗杆AB的高度为
20、（1）；（2）见解析.
21、所围矩形猪舍的长为1m、宽为8m
22、见解析
23、（1）；（2）80吨
24、51
25、（1）①y＝－10x＋700；②当该商品的售价是50元/件时，月销售利润最大，最大利润是4000元．（1）1.
26、（1）y＝﹣10x+700；（2）销售单价为45元时，每天可获得最大利润，最大利润为1元
售价x（元/件）
40
45
月销售量y（件）
300
250
月销售利润w（元）
3000
3750