四川省师大一中学2023-2024学年九上数学期末达标检测试题含答案

这是一份四川省师大一中学2023-2024学年九上数学期末达标检测试题含答案，共9页。试卷主要包含了考生必须保证答题卡的整洁，如图，空地上，下列函数的图象，不经过原点的是，下列标志中是中心对称图形的是等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．已知反比例函数的图象经过点，则这个函数的图象位于（ ）
A．第二、三象限B．第一、三象限C．第三、四象限D．第二、四象限
2．一5的绝对值是（ ）
A．5B．C．D．－5
3．如图，在平面直角坐标系中，Rt△ABO中，∠ABO=90°，OB边在x轴上，将△ABO绕点B顺时针旋转60°得到△CBD．若点A的坐标为（-2，2），则点C的坐标为（ ）
A．（，1）B．（1，）C．（1，2）D．（2，1）
4．如图，已知在△ABC中，P为AB上一点，连接CP，以下条件中不能判定△ACP∽△ABC的是（ ）
A．B．C．D．
5．如图，空地上（空地足够大）有一段长为10m的旧墙MN，小敏利用旧墙和木栏围成一个矩形菜园ABCD，已知木栏总长100m，矩形菜园ABCD的面积为900m1．若设AD＝xm，则可列方程（ ）
A．（60﹣）x＝900B．（60﹣x）x＝900C．（50﹣x）x＝900D．（40﹣x）x＝900
6．在一个不透明的盒子中装有个白球,若于个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为,则黄球的个数为( )
A．B．C．D．
7．函数y＝ax2与y＝﹣ax+b的图象可能是（ ）
A．B．
C．D．
8．已知袋中有若干个球，其中只有2个红球，它们除颜色外其它都相同．若随机从中摸出一个，摸到红球的概率是，则袋中球的总个数是（ ）
A．2B．4C．6D．8
9．下列函数的图象，不经过原点的是（ ）
A．B．y＝2x2C．y＝（x﹣1）2﹣1D．
10．下列标志中是中心对称图形的是（ ）
A．B．C．D．
二、填空题(每小题3分,共24分)
11．如图,港口A在观测站O的正东方向,OA=4.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为____.

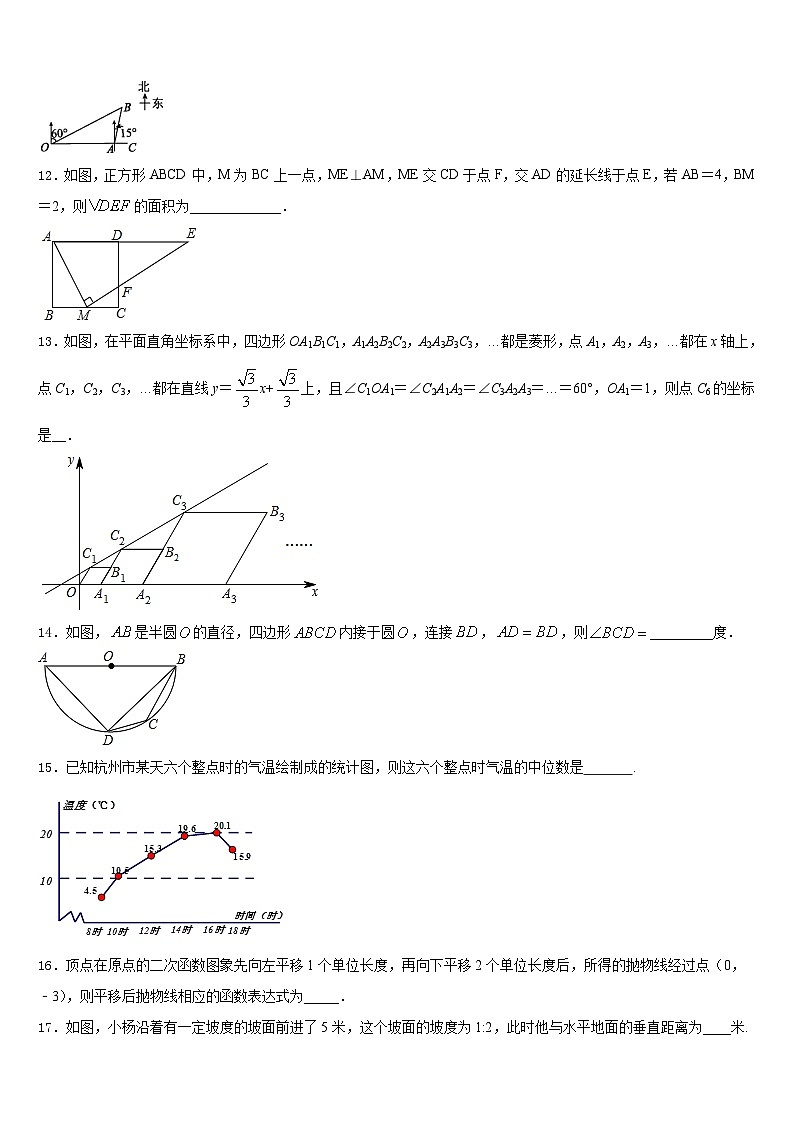
12．如图，正方形ABCD中，M为BC上一点，ME⊥AM，ME交CD于点F，交AD的延长线于点E，若AB＝4，BM＝2，则的面积为_____________．
13．如图，在平面直角坐标系中，四边形OA1B1C1，A1A2B2C2，A2A3B3C3，…都是菱形，点A1，A2，A3，…都在x轴上，点C1，C2，C3，…都在直线y＝x+上，且∠C1OA1＝∠C2A1A2＝∠C3A2A3＝…＝60°，OA1＝1，则点C6的坐标是__．
14．如图，是半圆的直径，四边形内接于圆，连接，，则_________度．
15．已知杭州市某天六个整点时的气温绘制成的统计图，则这六个整点时气温的中位数是 .
16．顶点在原点的二次函数图象先向左平移1个单位长度，再向下平移2个单位长度后，所得的抛物线经过点（0，﹣3），则平移后抛物线相应的函数表达式为_____．
17．如图，小杨沿着有一定坡度的坡面前进了5米，这个坡面的坡度为1:2，此时他与水平地面的垂直距离为____米.
18．若点P(3，1)与点Q关于原点对称，则点Q的坐标是___________．
三、解答题(共66分)
19．（10分）问题提出：
如图1，在等边△ABC中，AB＝9，⊙C半径为3，P为圆上一动点，连结AP，BP，求AP+BP的最小值
(1)尝试解决：
为了解决这个问题，下面给出一种解题思路，通过构造一对相似三角形，将BP转化为某一条线段长，具体方法如下：(请把下面的过程填写完整)
如图2，连结CP，在CB上取点D，使CD＝1，则有
又∵∠PCD＝∠
△ ∽△
∴
∴PD＝BP
∴AP+BP＝AP+PD
∴当A，P，D三点共线时，AP+PD取到最小值
请你完成余下的思考，并直接写出答案：AP+BP的最小值为 ．
(2)自主探索：
如图3，矩形ABCD中，BC＝6，AB＝8，P为矩形内部一点，且PB＝1，则AP+PC的最小值为 ．(请在图3中添加相应的辅助线)
(3)拓展延伸：
如图1，在扇形COD中，O为圆心，∠COD＝120°，OC＝1．OA＝2，OB＝3，点P是上一点，求2PA+PB的最小值，画出示意图并写出求解过程．
20．（6分）已知：如图，抛物线y＝ax2+bx+3与坐标轴分别交于点A，B（﹣3，0），C（1，0），点P是线段AB上方抛物线上的一个动点．
（1）求抛物线解析式；
（2）当点P运动到什么位置时，△PAB的面积最大？
（3）过点P作x轴的垂线，交线段AB于点D，再过点P作PE∥x轴交抛物线于点E，连接DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求点P的坐标；若不存在，说明理由．
21．（6分）如图，某小区规划在一个长，宽的矩形场地上，修建两横两竖四条同样宽的道路，且横、竖道路分别与矩形的长、宽平行，其余部分种草坪，若使每块草坪的面积都为.应如何设计道路的宽度？
22．（8分）如图，点A、B、C、D是⊙O上的四个点，AD是⊙O的直径，过点C的切线与AB的延长线垂直于点E，连接AC、BD相交于点F．
（1）求证：AC平分∠BAD；
（2）若⊙O的半径为，AC＝6，求DF的长．
23．（8分）从﹣1，﹣3，2，4四个数字中任取一个，作为点的横坐标，不放回，再从中取一个数作为点的纵坐标，组成一个点的坐标．请用画树状图或列表的方法列出所有可能的结果，并求该点在第二象限的概率．
24．（8分）如图，CD是一高为4米的平台，AB是与CD底部相平的一棵树，在平台顶C点测得树顶A点的仰角，从平台底部向树的方向水平前进3米到达点E，在点E处测得树顶A点的仰角，求树高AB(结果保留根号).
25．（10分）如图，A，B，C三点的坐标分别为A(1，0)，B(4，3)，C(5，0)，试在原图上画出以点A为位似中心，把△ABC各边长缩小为原来的一半的图形，并写出各顶点的坐标．
26．（10分）抛物线与轴交于两点（点在点的左侧），与轴交于点.已知，抛物线的对称轴交轴于点.
（1）求出的值；
（2）如图1，连接，点是线段下方抛物线上的动点，连接.点分别在轴，对称轴上，且轴.连接.当的面积最大时，请求出点的坐标及此时的最小值；
（3）如图2，连接，把按照直线对折，对折后的三角形记为，把沿着直线的方向平行移动，移动后三角形的记为，连接，，在移动过程中，是否存在为等腰三角形的情形？若存在，直接写出点的坐标；若不存在，请说明理由.
参考答案
一、选择题(每小题3分,共30分)
1、D
2、A
3、B
4、C
5、B
6、B
7、B
8、D
9、D
10、B
二、填空题(每小题3分,共24分)
11、1
12、1
13、（47，）
14、1
15、15.6
16、y＝﹣（x+1）2﹣2
17、
18、 (–3，–1)
三、解答题(共66分)
19、（1）BCP，PCD，BCP，；（2）2；（3）作图与求解过程见解析，2PA+PB的最小值为．
20、（1）y＝﹣x2﹣2x+3 （2）（﹣，） （3）存在，P（﹣2，3）或P（，）
21、道路的宽度应设计为1m.
22、（1）证明见解析；（2）．
23、表见解析，
24、6+
25、各顶点坐标分别为A(1，0)，B′(2.5，1.5)，C′(3，0)或A(1，0)，B″(－0.5，－1.5)，C″(－1，0)．
26、（1）；（2），最小值为；（3）或或或或.