广东省汕头市濠江区2023-2024学年数学九年级第一学期期末监测试题含答案

这是一份广东省汕头市濠江区2023-2024学年数学九年级第一学期期末监测试题含答案，共8页。试卷主要包含了平面直角坐标系内与点P等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
请考生注意：
1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。
一、选择题(每小题3分,共30分)
1．若在“正三角形、平行四边形、菱形、正五边形、正六边形”这五种图形中随机抽取一种图形，则抽到的图形属于中心对称图形的概率是( )
A．B．C．D．
2．如图，在△ABC中，点D是BC的中点，点E是AC的中点，若DE=3，则AB等于( )
A．4B．5C．5.5D．6
3．用频率估计概率，可以发现，某种幼树在一定条件下移植成活的概率为0.9，下列说法正确的是（ ）
A．种植10棵幼树，结果一定是“有9棵幼树成活”
B．种植100棵幼树，结果一定是“90棵幼树成活”和“10棵幼树不成活”
C．种植10n棵幼树，恰好有“n棵幼树不成活”
D．种植n棵幼树，当n越来越大时，种植成活幼树的频率会越来越稳定于0.9
4．如图，矩形ABCD的顶点D在反比例函数（x＜0）的图象上，顶点B，C在x轴上，对角线AC的延长线交y轴于点E，连接BE，若△BCE的面积是6，则k的值为（ ）
A．﹣6B．﹣8C．﹣9D．﹣12
5．已知二次函数，当时随的增大而减小，且关于的分式方程的解是自然数，则符合条件的整数的和是（ ）
A．3B．4C．6D．8
6．如图，在△ABC中，M，N分别是边AB，AC的中点，则△AMN的面积与四边形MBCN的面积比为
A．B．C．D．
7．如图，在矩形COED中，点D的坐标是(1，3)，则CE的长是（ ）
A．3B．C．D．4
8．平面直角坐标系内与点P（﹣2，3）关于原点对称的点的坐标是（ ）
A．（3，﹣2）B．（2，3）C．（2，﹣3）D．（﹣3，﹣3）
9．已知点是线段的黄金分割点，且，，则长是（ ）
A．B．C．D．
10．如图，将绕点按逆时针方向旋转后得到，若，则的度数为( )
A．B．C．D．
二、填空题(每小题3分,共24分)
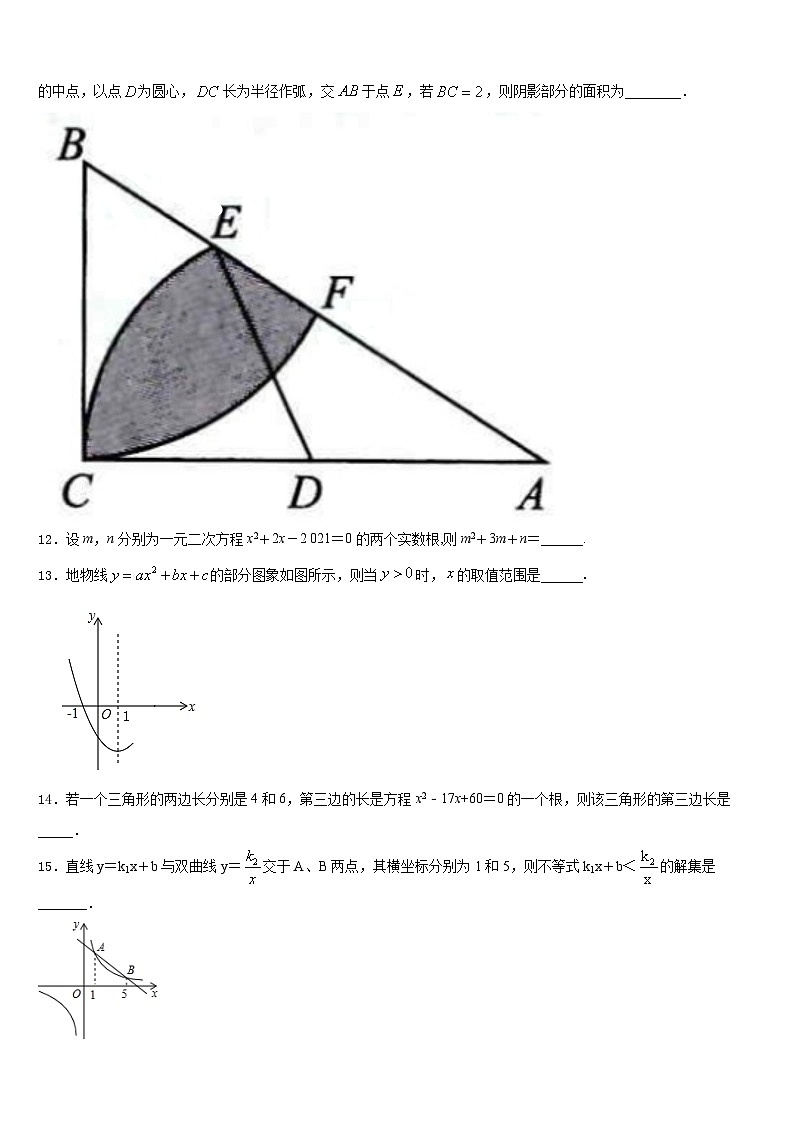
11．如图在中，，，以点为圆心，的长为半径作弧，交于点，为的中点，以点为圆心，长为半径作弧，交于点，若，则阴影部分的面积为________．
12．设m，n分别为一元二次方程x2＋2x－2 021＝0的两个实数根,则m2＋3m＋n＝______.
13．地物线的部分图象如图所示，则当时，的取值范围是______．
14．若一个三角形的两边长分别是4和6，第三边的长是方程x2﹣17x+60＝0的一个根，则该三角形的第三边长是_____．
15．直线y＝k1x＋b与双曲线y＝交于A、B两点，其横坐标分别为1和5，则不等式k1x＋b＜的解集是_______．
16．如图，在△ABC中，∠ACB＝90°，点D、E分别在边AC、BC上，且∠CDE＝∠B，将△CDE沿DE折叠,点C恰好落在AB边上的点F处，若AC＝2BC，则的值为____.
17．若反比例函数的图象经过点(2，﹣2)，(m，1)，则m＝_____．
18．如果两个相似三角形的面积的比是4：9，那么它们对应的角平分线的比是_____．
三、解答题(共66分)
19．（10分）一个不透明的口袋中装有4个分别标有数1，2，3，4的小球，它们的形状、大小完全相同，小红先从口袋里随机摸出一个小球记下数为x，小颖在剩下的3个球中随机摸出一个小球记下数为y，这样确定了点P的坐标（x，y）．
（1）小红摸出标有数3的小球的概率是 ．
（2）请你用列表法或画树状图法表示出由x，y确定的点P（x，y）所有可能的结果．
（3）求点P（x，y）在函数y＝﹣x+5图象上的概率．
20．（6分）如图1，抛物线与轴交于，两点，与轴交于点，已知点，且对称轴为直线．
（1）求该抛物线的解析式；
（2）点是第四象限内抛物线上的一点，当的面积最大时，求点的坐标；
（3）如图2，点是抛物线上的一个动点，过点作轴，垂足为．当时，直接写出点的坐标．
21．（6分）已知反比例函数的图像经过点（2，-3）．
（1）求这个函数的表达式．
（2）点（-1，6），（3，2）是否在这个函数的图像上？
（3）这个函数的图像位于哪些象限？函数值y随自变量的增大如何变化？
22．（8分）已知的半径为，点到直线的距离为，且直线与相切，若，分别是方程的两个根，求的值．
23．（8分）如图，反比例函数y＝（k≠0，x＞0）的图象与矩形OABC的边AB、BC分别交于点E、F，E（，6），且E为BC的中点，D为x轴负半轴上的点．
（1）求反比倒函数的表达式和点F的坐标；
（2）若D（﹣，0），连接DE、DF、EF，则△DEF的面积是 ．
24．（8分）如图，Rt△ABC中，∠C＝90°，E是AB边上一点，D是AC边上一点，且点D不与A、C重合，ED⊥AC．
（1）当sinB=时，
①求证：BE＝2CD．
②当△ADE绕点A旋转到如图2的位置时（45°＜∠CAD＜90°）．BE＝2CD是否成立？若成立，请给出证明；若不成立．请说明理由．
（2）当sinB=时，将△ADE绕点A旋转到∠DEB＝90°，若AC＝10，AD＝2，求线段CD的长．
25．（10分）如图，已知AB是⊙O的直径，AC为弦，且平分∠BAD，AD⊥CD，垂足为D．
(1) 求证：CD是⊙O的切线；
(2) 若⊙O的直径为4，AD=3，试求∠BAC的度数．
26．（10分）如图，在平面直角坐标系中，已知抛物线与直线都经过、两点，该抛物线的顶点为C．
（1）求此抛物线和直线的解析式；
（2）设直线与该抛物线的对称轴交于点E，在射线上是否存在一点M，过M作x轴的垂线交抛物线于点N，使点M、N、C、E是平行四边形的四个顶点？若存在，求点M的坐标；若不存在，请说明理由；
（3）设点P是直线下方抛物线上的一动点，当面积最大时，求点P的坐标，并求面积的最大值．
参考答案
一、选择题(每小题3分,共30分)
1、C
2、D
3、D
4、D
5、A
6、B
7、C
8、C
9、C
10、A
二、填空题(每小题3分,共24分)
11、
12、1.
13、或
14、1
15、0＜x＜1或x＞1．
16、
17、-1
18、2:1
三、解答题(共66分)
19、（1）；（2）共12种情况；（3）
20、（1）；（2）（3）或或或
21、（1）y=-；（2）(-1，6)在函数图像上，(3，2)不在函数图像上；（3）二、四象限，在每个象限内，y随x的增大而增大．
22、
23、（1）y＝，F（3，3）；（2）S△DEF＝1．
24、（1）①证明见解析；②BE＝2CD成立.理由见解析；（2）2或4．
25、（1）证明见解析；（2）30°.
26、（1）抛物线的解析式为，直线的解析式为，（2）或．（3）当时，面积的最大值是，此时P点坐标为．