

江苏省镇江市镇江中学2023-2024学年数学九年级第一学期期末质量检测模拟试题含答案
展开
这是一份江苏省镇江市镇江中学2023-2024学年数学九年级第一学期期末质量检测模拟试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,如图,如图,是的直径,、是弧等内容,欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.在Rt△ABC中,∠C=90°,、、所对的边分别为a、b、c,如果a=3b,那么∠A的余切值为( )
A.B.3C.D.
2.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点M是AB上的一点,点N是CB上的一点,,当∠CAN与△CMB中的一个角相等时,则BM的值为( )
A.3或4B.或4C.或6D.4或6
3.关于抛物线y=x2﹣4x+4,下列说法错误的是( )
A.开口向上
B.与x轴有两个交点
C.对称轴是直线线x=2
D.当x>2时,y随x的增大而增大
4.如图.已知的半径为3,,点为上一动点.以为边作等边,则线段的长的最大值为( )
A.9B.11C.12D.14
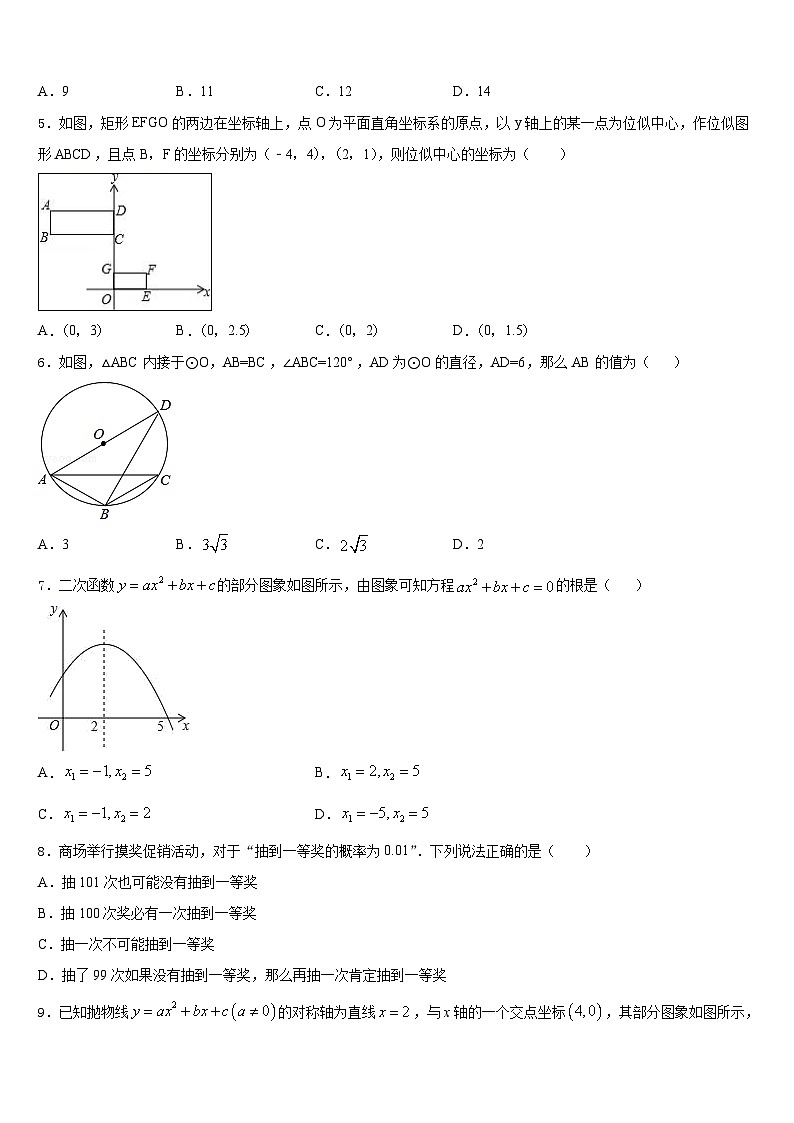
5.如图,矩形EFGO的两边在坐标轴上,点O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(﹣4,4),(2,1),则位似中心的坐标为( )
A.(0,3)B.(0,2.5)C.(0,2)D.(0,1.5)
6.如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那么AB的值为( )
A.3B.C.D.2
7.二次函数的部分图象如图所示,由图象可知方程的根是( )
A.B.
C.D.
8.商场举行摸奖促销活动,对于“抽到一等奖的概率为0.01”.下列说法正确的是( )
A.抽101次也可能没有抽到一等奖
B.抽100次奖必有一次抽到一等奖
C.抽一次不可能抽到一等奖
D.抽了99次如果没有抽到一等奖,那么再抽一次肯定抽到一等奖
9.已知抛物线的对称轴为直线,与x轴的一个交点坐标,其部分图象如图所示,下列结论:抛物线过原点;;;抛物线的顶点坐标为;当时,y随x增大而增大其中结论正确的是
A.B.C.D.
10.如图,是的直径,、是弧(异于、)上两点,是弧上一动点,的角平分线交于点,的平分线交于点.当点从点运动到点时,则、两点的运动路径长的比是( )
A.B.C.D.
二、填空题(每小题3分,共24分)
11.等腰△ABC的腰长与底边长分别是方程x2﹣6x+8=0的两个根,则这个△ABC的周长是_____.
12.分解因式:x3﹣16x=______.
13.设、是关于的方程的两个根,则__________.
14.如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tanC=_____.
15.如图所示:点A是反比例函数,图像上的点,AB⊥x轴于点B,AC⊥y轴于点C,,则k=______.
16.如图,边长为的正方形网格中,的顶点都在格点上,则的面积为_______ ; 若将绕点顺时针旋转,则顶点所经过的路径长为__________.
17.在Rt△ABC 中,∠C是直角,sinA=,则csB=__________
18.如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=1.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=;④S△DEF=4.
其中正确的是 (写出所有正确结论的序号).
三、解答题(共66分)
19.(10分)如图,已知△ABC,∠A=60°,AB=6,AC=1.
(1)用尺规作△ABC的外接圆O;
(2)求△ABC的外接圆O的半径;
(3)求扇形BOC的面积.
20.(6分)某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温和时间的关系如下图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想再8:10上课前能喝到不超过40℃的开水,问他需要在什么时间段内接水.
21.(6分)如图,在中,,,,点分别是边的中点,连接.将绕点顺时针方向旋转,记旋转角为.
① ②
③ ④
(1)问题发现:当时, .
(2)拓展探究:试判断:当时,的大小有无变化?请仅就图②的情况给出证明.
(3)问题解决:当旋转至三点共线时,如图③,图④,直接写出线段的长.
22.(8分)倡导全民阅读,建设书香社会.
(调查)目前,某地纸媒体阅读率为40%,电子媒体阅读率为80%,综合媒体阅读率为90%.
(百度百科)某种媒体阅读率,指有某种媒体阅读行为人数占人口总数的百分比;综合阅读率,在纸媒体和电子体中,至少有一种阅读行为的人数占人口总数的百分比,它反映了一个国家或地区的阅读水平.
(问题解决)(1)求该地目前只有电子媒体阅读行为人数占人口总数的百分比;
(2)国家倡导全民阅读,建设书香社会.预计未来两个五年中,若该地每五年纸媒体阅读人数按百分数x减少,综合阅读人数按百分数x增加,这样十年后,只读电子媒体的人数比目前增加53%,求百分数x.
23.(8分)如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为,AB=4.
(1)求点B,P,C的坐标;
(2)求证:CD是⊙P的切线.
24.(8分)计算:(1);
(2)先化简,再求值.,其中a=2020;
25.(10分)如图,已知⊙O为Rt△ABC的内切圆,切点分别为D,E,F,且∠C=90°,AB=13,BC=1.
(1)求BF的长;
(2)求⊙O的半径r.
26.(10分)文物探测队探测出某建筑物下面埋有文物,为了准确测出文物所在的深度,他们在文物上方建筑物的一侧地面上相距米的两处,用仪器测文物,探测线与地面的夹角分别是和, 求该文物所在位置的深度(精确到米) .
参考答案
一、选择题(每小题3分,共30分)
1、A
2、D
3、B
4、B
5、C
6、A
7、A
8、A
9、C
10、A
二、填空题(每小题3分,共24分)
11、11
12、x(x+4)(x–4).
13、1
14、.
15、
16、3.5;
17、
18、①②④.
三、解答题(共66分)
19、(1)见解析;(2);(3)
20、(1)当0≤x≤8时,y=10x+20;当8<x≤a时,y=;(2)40;(3)要在7:50~8:10时间段内接水.
21、(1);(2)无变化,理由见解析;(3)图③中;图④中;
22、(1)该社区有电子媒体阅读行为人数占人口总数的百分比为50%.(2)x为10%.
23、(1)C(-2,2);(2)证明见解析.
24、(1);(2),1.
25、(1)BF=3;(2)r=2.
26、17.3米
相关试卷
这是一份江苏省镇江市镇江实验学校2023-2024学年数学九上期末质量检测模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,下列说法正确的是,下列事件中,必然事件是等内容,欢迎下载使用。
这是一份2023-2024学年江苏省镇江市九上数学期末质量检测模拟试题含答案,共8页。试卷主要包含了若一次函数y=ax+b,若,设,,,则、、的大小顺序为等内容,欢迎下载使用。
这是一份2023-2024学年江苏省镇江市江南中学九年级数学第一学期期末检测模拟试题含答案,共7页。试卷主要包含了点P1,下列方程属于一元二次方程的是,关于x的一元二次方程x2+等内容,欢迎下载使用。









