江苏版高考物理一轮复习第4章第2节抛体运动课件

这是一份江苏版高考物理一轮复习第4章第2节抛体运动课件，文件包含39动能势能探究影响物体动能大小的因素教师版docx、39动能势能探究影响物体动能大小的因素学生版docx等2份试卷配套教学资源，其中试卷共68页， 欢迎下载使用。

一、平抛运动1．定义将物体以一定的初速度沿____________抛出，物体只在______作用下所做的运动。
2．性质加速度为_______________的匀变速曲线运动，轨迹是_________。3．条件：v0≠0，沿____________；只受______作用。
二、平抛运动的基本规律1．研究方法平抛运动可以分解为水平方向的____________运动和竖直方向的____________运动。2．基本规律
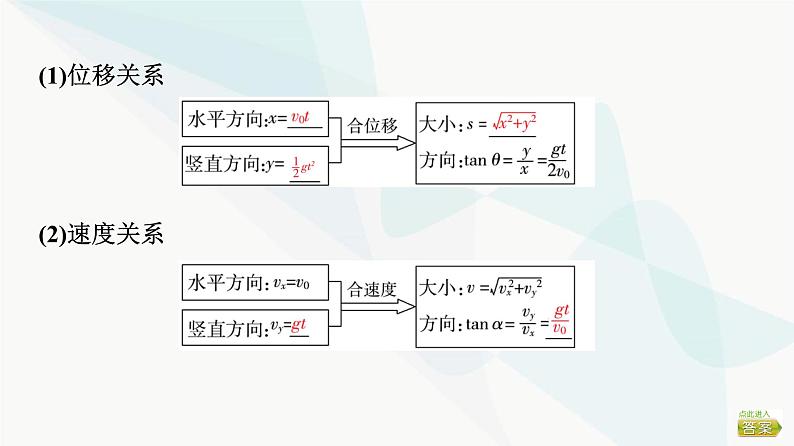
(1)位移关系(2)速度关系
三、斜抛运动1．定义：将物体以初速度v0____________或斜向下方抛出，物体只在______作用下的运动。2．性质：斜抛运动是加速度为g的_________曲线运动，运动轨迹是_________。3．研究方法：运动的合成与分解(1)水平方向：______直线运动；(2)竖直方向：_________直线运动。
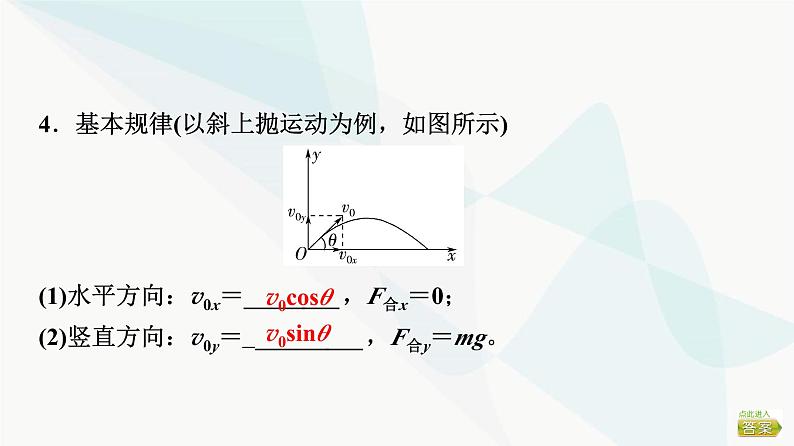
4．基本规律(以斜上抛运动为例，如图所示)(1)水平方向：v0x＝________，F合x＝0；(2)竖直方向：v0y＝__________，F合y＝mg。
一、易错易误辨析(正确的打“√”，错误的打“×”)(1)以一定的初速度水平抛出的物体的运动是平抛运动。(　　)(2)平抛运动的轨迹是抛物线，速度方向时刻变化，加速度方向也可能时刻变化。(　　)(3)两个做平抛运动的物体，初速度大的落地时速度大。(　　)(4)做平抛运动的物体初速度越大，在空中运动的时间越短。(　　)(5)无论初速度是斜向上方还是斜向下方的斜抛运动都是匀变速曲线运动。(　　)
二、教材习题衍生1.(平抛运动的基本规律)从距地面h高度水平抛出一小球，落地时速度方向与水平方向的夹角为θ，不计空气阻力，重力加速度为g，下列结论中正确的是(　　)
C．若小球初速度减为原来一半，则平抛运动的时间变为原来的两倍D．若小球初速度减为原来一半，则落地时速度方向与水平方向的夹角变为2θ[答案]　B
2．(平抛与斜面的结合)如图，轰炸机沿水平方向匀速飞行，到达山坡底端正上方时释放一颗炸弹，击中坡上的目标A。已知A点高度为h，山坡倾角为θ，重力加速度为g，由此不能算出的是(　　)A．轰炸机的飞行高度 B．轰炸机的飞行速度C．炸弹的飞行时间 D．炸弹投出时的动能
3．(斜抛运动规律的应用)由消防带水龙头的喷嘴喷出水的流量是0.28 m3/min，水离开喷口时的速度大小为16 m/s，方向与水平面夹角为60°，在最高处正好到达着火位置，忽略空气阻力，则空中水柱的高度和水量分别是(重力加速度g取10 m/s2)(　　)A．28.8 m　1.12×10－2 m3B．28.8 m　0.672 m3C．38.4 m　1.29×10－2 m3D．38.4 m　0.776 m3
1.(平抛规律的理解与应用)(2022·全国甲卷)将一小球水平抛出，使用频闪仪和照相机对运动的小球进行拍摄，频闪仪每隔0.05 s发出一次闪光。某次拍摄时，小球在抛出瞬间频闪仪恰好闪光，拍摄的照片编辑后如图所示。图中的第一个小球为抛出瞬间的影像，每相邻两个球之间被删去了3个影像，所标出的两个线段的长度s1和s2之比为3∶7。重力加速度大小g取10 m/s2，忽略空气阻力。求在抛出瞬间小球速度的大小。
考点1　平抛与斜抛运动的基本规律
[解析]　设s1对应的水平位移为x，对应的竖直位移为y，则根据平抛运动的特点可知，s2对应的水平位移也为x，对应的竖直位移为3y
2.(平抛运动推论的应用)将小球以某一初速度从A点水平向左抛出，运动轨迹如图所示，B为轨迹上的一点。改变抛出点位置，为使小球仍沿原方向经过B点，不计空气阻力，以下做法可能实现的是(　　)A．在A点左侧等高处以较小的初速度水平抛出小球B．在A点右侧等高处以较大的初速度水平抛出小球C．在A、B两点间轨迹上某点沿切线向左下方抛出小球D．在A、B两点间轨迹上某点以较小的初速度水平向左抛出小球
C　[根据平抛运动的推论，速度反向延长线过水平位移的中点，如图，在与A等高处其他位置水平抛出，无论左侧还是右侧，只要经过B点，则不满足平抛运动的推论，A、B项错误；当在A、B两点间轨迹上某点沿切线向左下方抛出小球，小球速度等于原小球经过该点的速度，则小球轨迹重合，小球能够沿原方向经过B点，C项正确；在A、B两点间轨迹上某点以较小的初速度水平向左抛出小球，根据几何关系可知：如果沿原方向经过B点，小球速度反向延长线不能过水平位移中点，D项错误。]
3.(不同高度平抛后落在同一水平面上的多体平抛问题)如图所示，小球A、B分别从2l和l的高度水平抛出后落地，上述过程中A、B的水平位移分别为l和2l。忽略空气阻力，则(　　)A．A和B的位移大小相等B．A的运动时间是B的2倍C．A的初速度是B的D．A的末速度比B的小
4.(同一高度平抛后落在同一竖直面上的多体平抛问题)(2022·江苏七市二模)如图所示，在飞镖比赛中，某同学将飞镖从O点水平抛出，第一次击中飞镖盘上的a点，第二次击中飞镖盘上的b点，忽略空气阻力，则(　　)A．飞镖第一次水平抛出的速度较小B．飞镖第二次抛出时的动能较小C．飞镖两次在空中运动的时间相等D．飞镖两次击中飞镖盘时的速度方向相同
5．(斜抛问题)(2022·山东卷变式)如图所示，某同学将离地1.25 m的网球以13 m/s的速度斜向上击出，击球点到竖直墙壁的距离4.8 m。当网球竖直分速度为零时，击中墙壁上离地高度为8.45 m的P点，网球与墙壁碰撞后，垂直墙面速度分量大小变为碰前的0.75倍，平行墙面的速度分量不变，重力加速度g取10 m/s2，网球碰墙后的速度大小v和着地点到墙壁的距离d分别为(　　)
1．对平抛运动的约束条件常见的有“斜面”约束和“曲面”约束，解此类问题的关键：(1)灵活运用平抛运动的位移和速度分解方法。(2)充分运用斜面倾角，找出斜面倾角与位移偏向角、速度偏向角的关系。(3)“曲面”约束类要灵活应用平抛运动的推论。
考点2　有约束条件的平抛运动
[典例]　(从斜面平抛且落点在斜面上)(一题多法)如图所示，一名跳台滑雪运动员经过一段时间的加速滑行后从O点水平飞出，经过3 s落到斜坡上的A点。已知O点是斜坡的起点，斜坡与水平面的夹角θ＝37°，运动员的质量m＝50 kg，不计空气阻力(sin 37°＝0.6，cs 37°＝0.8，g取10 m/s2)。求：(1)A点与O点的距离L；(2)运动员离开O点时的速度大小；(3)运动员从O点飞出到离斜坡距离最远所用的时间。
(3)方法一：运动员的平抛运动可分解为沿斜面方向的匀加速运动(初速度为v0cs 37°、加速度为gsin 37°)和垂直斜面方向的类竖直上抛运动(初速度为v0sin 37°、加速度为gcs 37°)。当垂直斜面方向的速度减为零时，运动员离斜坡最远，有v0sin 37°＝gcs 37°·t，解得t＝1.5 s。
[答案]　(1)75 m　(2)20 m/s　(3)1.5 s
A．斜面的倾角是60°B．小球的抛出点距斜面的竖直高度是15 mC．若将小球以水平速度v′0＝5 m/s向右抛出，它一定落在AB的中点P的上方D．若将小球以水平速度v′0＝5 m/s向右抛出，它一定落在AB的中点P处
2．(2018·全国卷Ⅲ)在一斜面顶端，将甲、乙两个小球分别以v和的速度沿同一方向水平抛出，两球都落在该斜面上。甲球落至斜面时的速率是乙球落至斜面时速率的(　　)A．2倍 B．4倍 C．6倍 D．8倍
A　[甲、乙两球都落在同一斜面上，则隐含做平抛运动的甲、乙的最终位移方向相同，根据位移方向与末速度方向的关系，即末速度方向与水平方向夹角的正切值是位移方向与水平方向夹角的正切值的2倍，可得它们的末速度方向也相同，在速度矢量三角形中，末速度比值等于初速度比值，故A正确。]
3.如图所示，从倾角为θ且足够长的斜面的顶点A，先后将同一小球以不同的初速度水平向右抛出，第一次初速度为v1，小球落到斜面上前一瞬间的速度方向与斜面的夹角为φ1，第二次初速度为v2，小球落在斜面上前一瞬间的速度方向与斜面间的夹角为φ2，若v2>v1，则φ1和φ2的大小关系是(　　)A．φ1＞φ2 B．φ1＜φ2C．φ1＝φ2 D．无法确定
C　[根据平抛运动的推论，做平抛(或类平抛)运动的物体在任一时刻或任一位置时，设其速度方向与水平方向的夹角为α，位移与水平方向的夹角为β，则tan α＝2tan β。由上述关系式结合题图中的几何关系可得：tan(φ＋θ)＝2tan θ，此式表明小球的速度方向与斜面间的夹角φ仅与θ有关，而与初速度无关，因此φ1＝φ2，即以不同初速度平抛的物体，落在斜面上各点的速度方向是互相平行的。故C正确。]
4.(2023·南京市高三调研)如图所示，固定斜面PO、QO与水平面MN的夹角均为45°，现由PO斜面上的A点分别以速度v1、v2先后沿水平方向抛出两个小球(可视为质点)，不计空气阻力，其中以v1抛出的小球恰能垂直于QO落于C点，飞行时间为t，以v2抛出的小球落在PO斜面上的B点，且B、C在同一水平面上，则(　　)
5.如图所示，从O点以水平初速度v1、v2抛出两个小球(可视为质点)，最终它们分别落在圆弧上的A点和B点，已知OA与OB互相垂直，且OA与竖直方向成α角，不计空气阻力，则两小球初速度之比v1∶v2为(　　)A．tan α B．cs α
6.(2023·宜兴中学模拟)如图所示，竖直平面内平抛的小球恰好与光滑半圆轨道相切于B点，已知抛出点在半圆轨道左端点(A点)的正上方，半圆轨道半径为R，直线OB与水平面成60°角，重力加速度为g，则下列关于小球在空中的运动的分析正确的是(　　)
平抛中常见的“三种”临界特征(1)有些题目中有“刚好”“恰好”“正好”等字眼，明显表明题述的过程中存在着临界点。(2)若题目中有“取值范围”“多长时间”“多大距离”等词语，表明题述的过程中存在着“起止点”，而这些起止点往往就是临界点。(3)若题目中有“最大”“最小”“至多”“至少”等字眼，表明题述的过程中存在着极值，这个极值点往往是临界点。
考点3　平抛中的临界、极值问题
[典例]　(排球平抛运动的临界和极值问题)排球场总长18 m，网高2.25 m，如图所示，设对方飞来一球，刚好在3 m线正上方被我方运动员击回。假设排球被击回的初速度方向是水平的，那么可认为排球被击回时做平抛运动。(g取10 m/s2)
(1)若击球的高度h＝2.5 m，球击回的水平速度与底线垂直，球既不能触网又不出底线，则球被击回的水平速度在什么范围内？(结果可用根号表示)(2)若运动员仍从3 m线处起跳，击球高度h满足一定条件时，会出现无论球的水平速度多大都是触网或越界，试求h满足的条件。
h′＝h－2.25 m由此得h＝2.4 m故若h<2.4 m，无论击球的速度多大，球总是触网或越界。
(1)确定研究对象的运动性质。(2)根据题意确定临界状态。(3)确定临界轨迹，画出轨迹示意图。(4)应用平抛运动的规律，结合临界条件列方程求解。
[跟进训练] 1．一带有乒乓球发射机的乒乓球台如图所示。水平台面的长和宽分别为L1和L2，中间球网高度为h。发射机安装于台面左侧边缘的中点，能以不同速率向右侧不同方向水平发射乒乓球，发射点距台面高度为3h。不计空气的作用，重力加速度大小为g。若乒乓球的发射速率v在某范围内，通过选择合适的方向，就能使乒乓球落到球网右侧台面上，则v的最大取值范围是(　　)
2．如图为某娱乐节目中某个比赛环节的示意图，参与比赛的选手会遇到一个人造山谷AOB，AO是高h＝3 m的竖直峭壁，OB是以A点为圆心的弧形坡，∠OAB＝60°，B点右侧是一段水平跑道。选手可以自A点借助绳索降到O点后再爬上跑道，但身体素质好的选手会选择自A点直接跃上跑道。选手可视为质点，忽略空气阻力，重力加速度g取10 m/s2。
(1)若选手以速度v0水平跳出后，恰好能落到水平跑道上，求v0的最小值；(2)若选手以速度v1＝4 m/s水平跳出，求该选手在空中的运动时间。