浙江省湖州市南浔区2023-2024学年九年级数学第一学期期末调研试题含答案

这是一份浙江省湖州市南浔区2023-2024学年九年级数学第一学期期末调研试题含答案，共7页。试卷主要包含了答题时请按要求用笔，如图，厂房屋顶人字架，下列几何体的三视图相同的是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1．下列命题正确的是( )
A．圆是轴对称图形，任何一条直径都是它的对称轴
B．平分弦的直径垂直于弦，并且平分弦所对的弧
C．相等的圆心角所对的弧相等，所对的弦相等
D．同弧或等弧所对的圆周角相等
2．如果，、分别对应、，且，那么下列等式一定成立的是（ ）
A．B．的面积：的面积
C．的度数：的度数D．的周长：的周长
3．把分式中的、都扩大倍，则分式的值（ ）
A．扩大倍B．扩大倍C．不变D．缩小倍
4．袋中有5个白球，x个红球，从中随机摸出一个球，恰为红球的概率为，则x为
A．25B．20C．15D．10
5．下列各式计算正确的是（ ）
A．2x•3x=6x B．3x-2x=x C．（2x）2=4x D．6x÷2x=3x
6．如图所示，在中，与相交于点，为的中点，连接并延长交于点，则与的面积比值为（ ）
A．B．C．D．
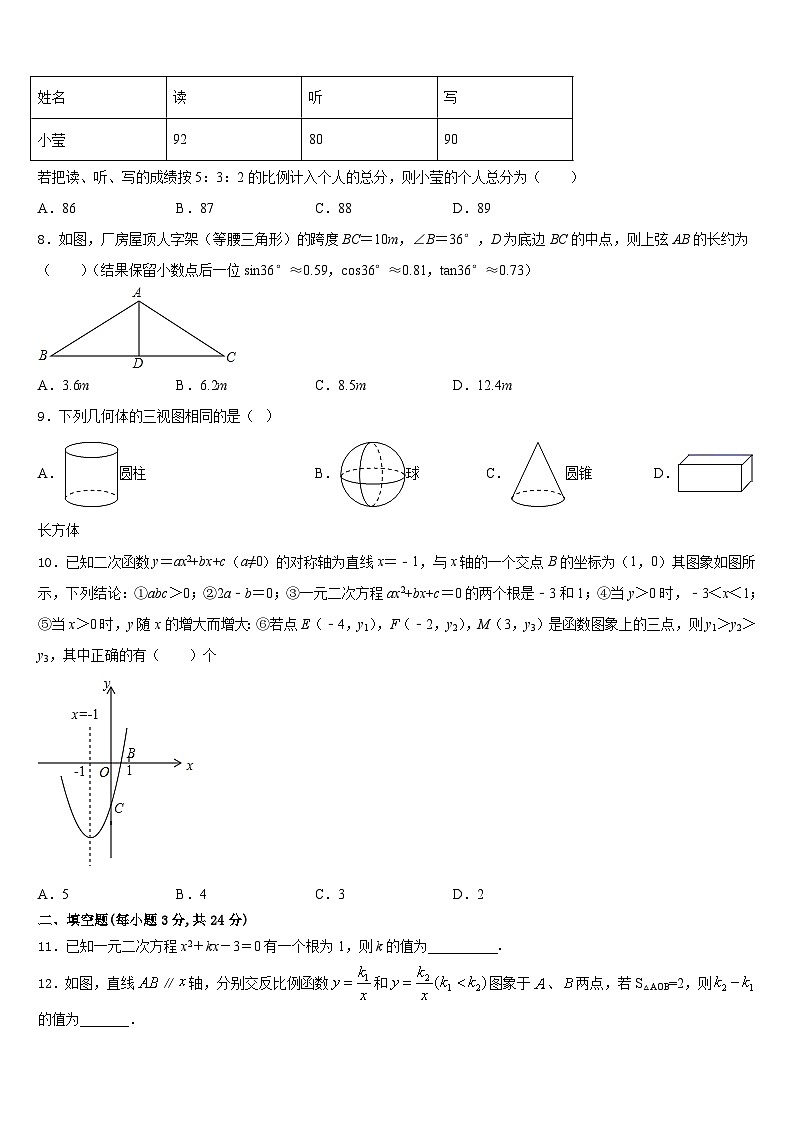
7．学校“校园之声”广播站要选拔一名英语主持人，小莹参加选拔的各项成绩如下：
若把读、听、写的成绩按5：3：2的比例计入个人的总分，则小莹的个人总分为（ ）
A．86B．87C．88D．89
8．如图，厂房屋顶人字架（等腰三角形）的跨度BC＝10m，∠B＝36°，D为底边BC的中点，则上弦AB的长约为（ ）（结果保留小数点后一位sin36°≈0.59，cs36°≈0.81，tan36°≈0.73）
A．3.6mB．6.2mC．8.5mD．12.4m
9．下列几何体的三视图相同的是（ ）
A．圆柱 B．球 C．圆锥 D．长方体
10．已知二次函数y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣1，与x轴的一个交点B的坐标为（1，0）其图象如图所示，下列结论：①abc＞0；②2a﹣b＝0；③一元二次方程ax2+bx+c＝0的两个根是﹣3和1；④当y＞0时，﹣3＜x＜1；⑤当x＞0时，y随x的增大而增大：⑥若点E（﹣4，y1），F（﹣2，y2），M（3，y3）是函数图象上的三点，则y1＞y2＞y3，其中正确的有（ ）个
A．5B．4C．3D．2
二、填空题(每小题3分,共24分)
11．已知一元二次方程x2＋kx－3＝0有一个根为1，则k的值为__________．
12．如图，直线∥轴，分别交反比例函数和图象于、两点，若S△AOB=2，则的值为_______．
13．一个口袋中装有10个红球和若干个黄球．在不允许将球倒出来数的前提下，为估计口袋中黄球的个数，小明采用了如下的方法：每次先从口袋中摸出10个球，求出其中红球数与10的比值，再把球放回口袋中摇匀．不断重复上述过程20次，得到红球数与10的比值的平均数为0.1．根据上述数据，估计口袋中大约有_______个黄球
14．如图，直线y＝k1x＋b与双曲线交于A、B两点，其横坐标分别为1和5，则不等式k1x＜＋b的解集是 ▲ ．
15．等边三角形中，，将绕的中点逆时针旋转，得到，其中点的运动路径为，则图中阴影部分的面积为__________．
16．如图，在中，点在边上，与边分别相切于两点，与边交于点，弦与平行，与的延长线交于点若点是的中点，，则的长为_____．
17．如图，让此转盘自由转动两次，两次指针都落在阴影部分区域（边界宽度忽略不记）的概率是____________.
18．请写出一个位于第一、三象限的反比例函数表达式，y = ．
三、解答题(共66分)
19．（10分）如图，抛物线y=ax2+bx+6经过点A（﹣2，0），B（4，0）两点，与y轴交于点C，点D是抛物线上一个动点，设点D的横坐标为m（1＜m＜4）连接BC，DB，DC．
（1）求抛物线的函数解析式；
（2）△BCD的面积是否存在最大值，若存在，求此时点D的坐标；若不存在，说明理由；
（3）在（2）的条件下，若点M是x轴上一动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B，D，M，N为顶点的四边形是平行四边形．若存在，请直接写出点M的坐标；若不存在，请说明理由．
20．（6分）如图，在△ABC中，DE∥BC，，M为BC上一点，AM交DE于N.
(1)若AE＝4，求EC的长；
(2)若M为BC的中点，S△ABC＝36，求S△ADN的值．
21．（6分）将矩形纸片沿翻折，使点落在线段上，对应的点为，若，求的长.
22．（8分）已知:如图，菱形中，点，分别在，边上，，连接，.求证:.
23．（8分）已知关于x的一元二次方程（a+c）x2+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．
（1）如果x=﹣1是方程的根，试判断△ABC的形状，并说明理由；
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
（3）如果△ABC是等边三角形，试求这个一元二次方程的根．
24．（8分）如图，在△ABC中，点P、D分别在边BC、AC上，PA⊥AB，垂足为点A，DP⊥BC，垂足为点P，．
（1）求证：∠APD＝∠C；
（2）如果AB＝3，DC＝2，求AP的长．
25．（10分）岚山区地处黄海之滨，渔业资源丰富，海产品深受消费者喜爱．某海产品批发超市对进货价为40元/千克的某品牌小黄鱼的销售情况进行统计，发现每天销售量y（千克）与销售价x（元/千克）存在一次函数关系，如图所示．
（1）求y关于x的函数关系式；
（2）若不考虑其它因素，则销售总利润=每千克的利润×总销量，那么当销售价格定为多少时，该品牌小黄鱼每天的销售利润最大？最大利润是多少？
26．（10分）用适当的方法解下列方程：
参考答案
一、选择题(每小题3分,共30分)
1、D
2、D
3、C
4、B
5、B
6、C
7、C
8、B
9、B
10、C
二、填空题(每小题3分,共24分)
11、2
12、1
13、2
14、－2＜x＜－1或x＞1．
15、
16、．
17、
18、（答案不唯一）.
三、解答题(共66分)
19、（1）；（2）存在，D的坐标为（2，6）；（3）存在这样的点M，使得以点B，D，M，N为顶点的四边形是平行四边形，点M的坐标为：（2，0）或（6，0）或（，0）或（，0）．
20、（1）2（2）8
21、10
22、见解析
23、 (1) △ABC是等腰三角形；(2)△ABC是直角三角形；(3) x1=0，x2=﹣1．
24、（1）见解析；（2）
25、（1）y=-2x+140；（2）当该种小黄鱼销售价定为55元/千克时，每天的销售利润有最大值1元
26、，．
姓名
读
听
写
小莹
92
80
90