浙江省绍兴上虞区四校联考2023-2024学年九年级数学第一学期期末统考试题含答案

这是一份浙江省绍兴上虞区四校联考2023-2024学年九年级数学第一学期期末统考试题含答案，共8页。试卷主要包含了抛物线y＝﹣2等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
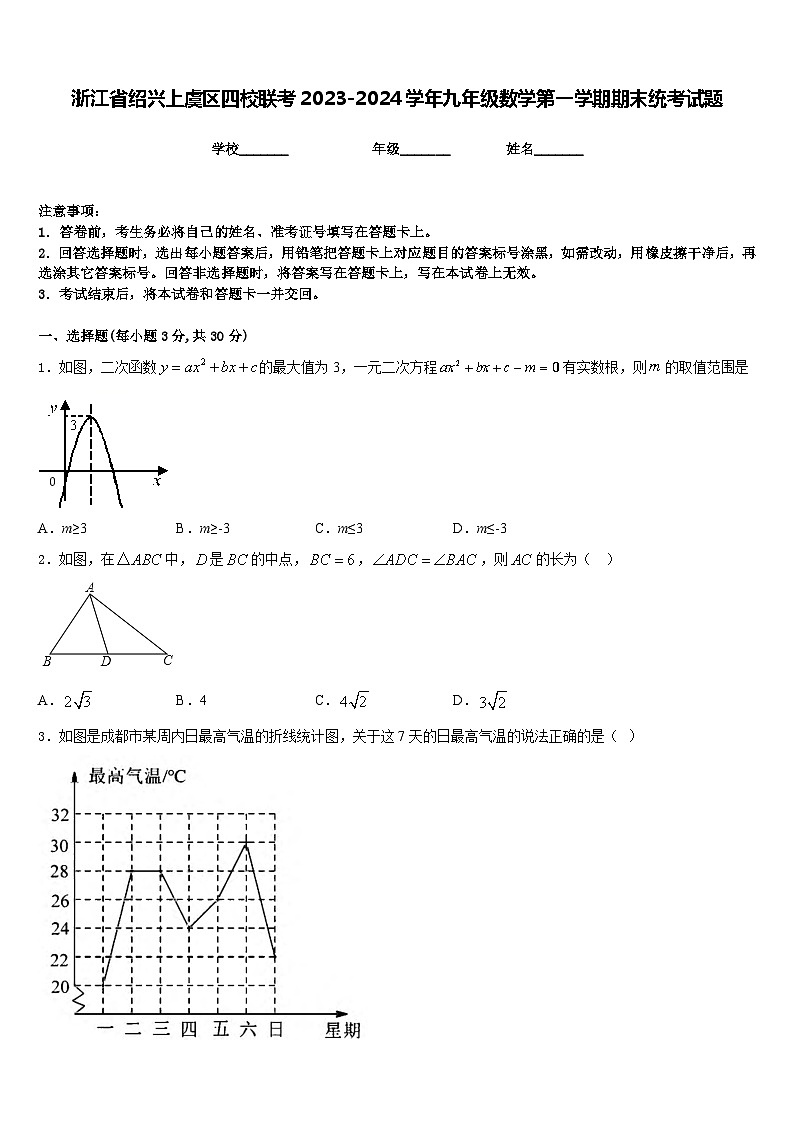
1．如图，二次函数的最大值为3，一元二次方程有实数根，则的取值范围是
A．m≥3B．m≥-3C．m≤3D．m≤-3
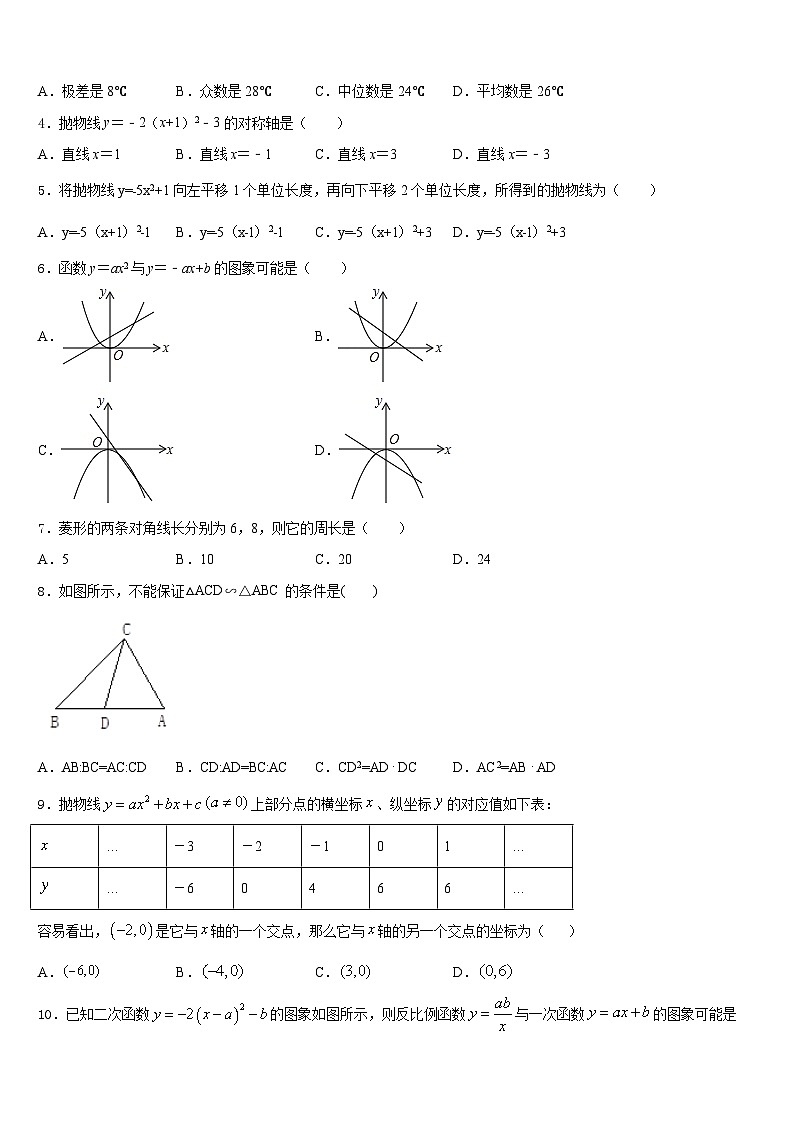
2．如图，在中，是的中点，，，则的长为（ ）
A．B．4C．D．
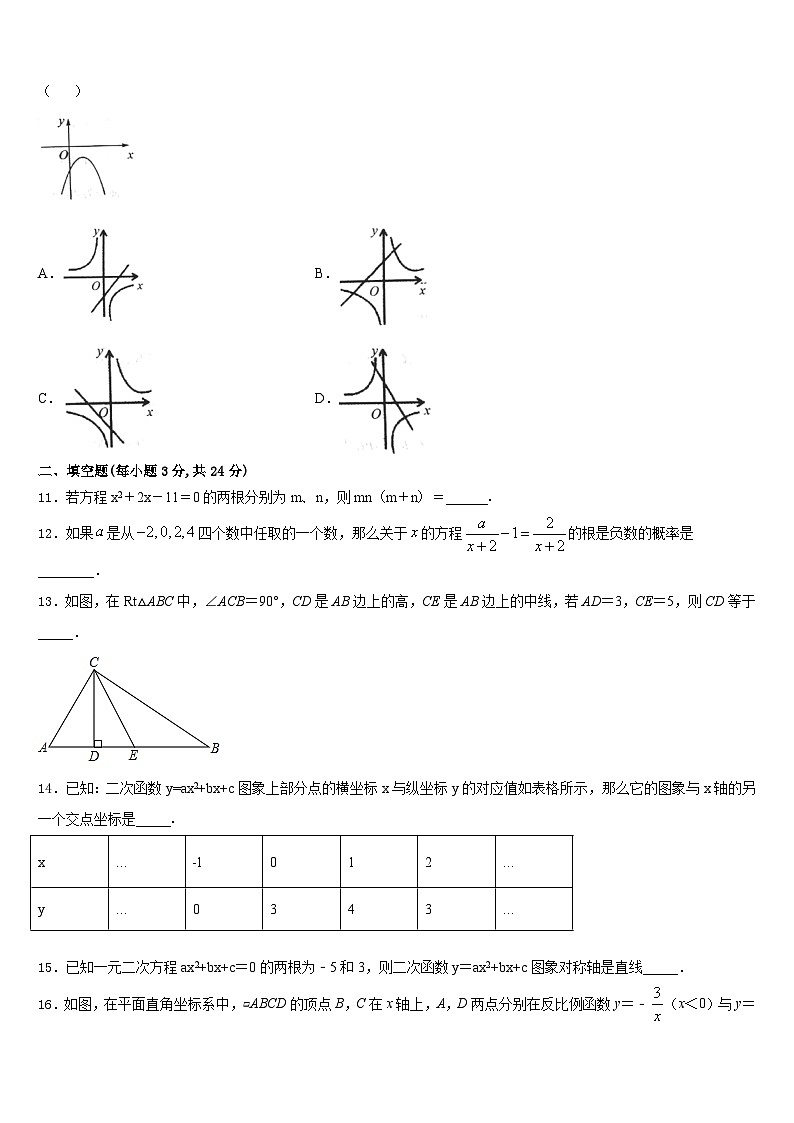
3．如图是成都市某周内日最高气温的折线统计图，关于这7天的日最高气温的说法正确的是（ ）
A．极差是8℃B．众数是28℃C．中位数是24℃D．平均数是26℃
4．抛物线y＝﹣2（x+1）2﹣3的对称轴是（ ）
A．直线x＝1B．直线x＝﹣1C．直线x＝3D．直线x＝﹣3
5．将抛物线y=﹣5x2+1向左平移1个单位长度，再向下平移2个单位长度，所得到的抛物线为（ ）
A．y=﹣5（x+1）2﹣1B．y=﹣5（x﹣1）2﹣1C．y=﹣5（x+1）2+3D．y=﹣5（x﹣1）2+3
6．函数y＝ax2与y＝﹣ax+b的图象可能是（ ）
A．B．
C．D．
7．菱形的两条对角线长分别为6，8，则它的周长是（ ）
A．5B．10C．20D．24
8．如图所示，不能保证△ACD∽△ABC的条件是( )
A．AB:BC=AC:CDB．CD:AD=BC:ACC．CD2=ADDCD．AC2=ABAD
9．抛物线上部分点的横坐标、纵坐标的对应值如下表：
容易看出，是它与轴的一个交点，那么它与轴的另一个交点的坐标为（ ）
A．B．C．D．
10．已知二次函数的图象如图所示，则反比例函数与一次函数的图象可能是 （ ）
A．B．
C．D．
二、填空题(每小题3分,共24分)
11．若方程x2＋2x－11＝0的两根分别为m、n，则mn（m＋n）＝______．
12．如果是从四个数中任取的一个数，那么关于的方程的根是负数的概率是________．
13．如图，在Rt△ABC中，∠ACB＝90°，CD是AB边上的高，CE是AB边上的中线，若AD＝3，CE＝5，则CD等于_____．
14．已知：二次函数y=ax2+bx+c图象上部分点的横坐标x与纵坐标y的对应值如表格所示，那么它的图象与x轴的另一个交点坐标是_____．
15．已知一元二次方程ax2+bx+c＝0的两根为﹣5和3，则二次函数y＝ax2+bx+c图象对称轴是直线_____．
16．如图，在平面直角坐标系中，▱ABCD的顶点B，C在x轴上，A，D两点分别在反比例函数y＝﹣（x＜0）与y＝（x＞0）的图象上，若▱ABCD的面积为4，则k的值为：_____．
17．Rt△ABC中，已知∠C＝90°，∠B＝50°，点D在边BC上，BD＝2CD（如图）．把△ABC绕着点D逆时针旋转m（0＜m＜180）度后，如果点B恰好落在初始Rt△ABC的边上，那么m＝______．
18．在直角坐标系中，点（﹣1，2）关于原点对称点的坐标是_____．
三、解答题(共66分)
19．（10分）如果是关于x的一元二次方程；
（1）求m的值;
（2）判断此一元二次方程的根的情况，如果有实数根则求出根，如果没有说明理由则可．
20．（6分）已知关于的一元二次方程有两个不相等的实数根
（1）求的取值范围；
（2）若为正整数，且该方程的根都是整数，求的值．
21．（6分）（1）解方程：x（x﹣3）＝x﹣3；
（2）用配方法解方程：x2﹣10x+6＝0
22．（8分）在平面直角坐标系中，已知抛物线.
（1）我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“方点”.试求拋物线的“方点”的坐标；
（2）如图，若将该抛物线向左平移1个单位长度，新抛物线与轴相交于、两点（在左侧），与轴相交于点，连接.若点是直线上方抛物线上的一点，求的面积的最大值；
（3）第（2）问中平移后的抛物线上是否存在点，使是以为直角边的直角三角形？若存在，直接写出所有符合条件的点的坐标；若不存在，说明理由.
23．（8分）已知：如图，抛物线y＝﹣x2+2x+3交x轴于点A、B，其中点A在点B的左边，交y轴于点C，点P为抛物线上位于x轴上方的一点．
（1）求A、B、C三点的坐标；
（2）若△PAB的面积为4，求点P的坐标．
24．（8分）如图，在△ABC中，AD是BC边上的中线，且AD=AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F．
(1)求证：△ABC∽△FCD；
(2)过点A作AM⊥BC于点M，求DE：AM的值；
(3)若S△FCD=5，BC=10，求DE的长．
25．（10分）如图，已知抛物线经过点、，且与轴交于点，抛物线的顶点为，连接，点是线段上的一个动点（不与、）重合.
（1）求抛物线的解析式，并写出顶点的坐标；
（2）过点作轴于点，求面积的最大值及取得最大值时点的坐标；
（3）在（2）的条件下，若点是轴上一动点，点是抛物线上一动点，试判断是否存在这样的点，使得以点，，，为顶点的四边形是平行四边若存在，请直接写出点的坐标：若不存在，请说明理由.
26．（10分）如图，在A港口的正东方向有一港口B．某巡逻艇从A港口沿着北偏东60°方向巡逻，到达C处时接到命令，立刻在C处沿东南方向以20海里/小时的速度行驶2小时到达港口B．求A，B两港之间的距离（结果保留根号）．
参考答案
一、选择题(每小题3分,共30分)
1、C
2、D
3、B
4、B
5、A
6、B
7、C
8、D
9、C
10、B
二、填空题(每小题3分,共24分)
11、22
12、
13、
14、（3，0）．
15、x＝﹣1
16、2
17、80°或120°
18、（1，﹣2）
三、解答题(共66分)
19、（1）m=1；（2）有两个不相等的实数根，，．
20、（1）k＜（1）1
21、（1）x＝3或x＝1；（2）x＝5
22、（1）抛物线的方点坐标是，；（2）当时，的面积最大，最大值为；（3）存在，或
23、（1）A（﹣1，0），B（3，0），C（0，3）；（2）P点坐标为（1﹣，2），（1+，2）
24、（1）证明见解析；（2）；（3）．
25、（1），D的坐标为（1，4）；（2）当m=时 △BPE的面积取得最大值为，P的坐标是（，3）；（3）存在，M点的坐标为；；；；；
26、A，B间的距离为（20+20）海里．
…
－3
－2
－1
0
1
…
…
－6
0
4
6
6
…
x
…
﹣1
0
1
2
…
y
…
0
3
4
3
…