湖北省来凤县2023-2024学年九上数学期末综合测试模拟试题含答案

这是一份湖北省来凤县2023-2024学年九上数学期末综合测试模拟试题含答案，共9页。试卷主要包含了考生要认真填写考场号和座位序号，如图，是用棋子摆成的“上”字等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。
一、选择题(每小题3分,共30分)
1．函数y=ax+b和y=ax2+bx+c（a≠0）在同一个坐标系中的图象可能为（ ）
A．B．
C．D．
2．如图，菱形中，，，且，连接交对角线于．则的度数是（ ）
A．100°B．105°C．120°D．135°
3．已知抛物线的对称轴为直线，与x轴的一个交点坐标，其部分图象如图所示，下列结论：抛物线过原点；；；抛物线的顶点坐标为；当时，y随x增大而增大其中结论正确的是
A．B．C．D．
4．抛物线经过平移得到抛物线,平移过程正确的是（ ）
A．先向下平移个单位,再向左平移个单位
B．先向上平移个单位,再向右平移个单位
C．先向下平移个单位,再向右平移个单位
D．先向上平移个单位,再向左平移个单位.
5．下列关于x 的一元二次方程，有两个不相等的实数根的方程的是( )
A．x2＋1＝0B．x2＋2x＋1＝0C．x2＋2x＋3＝0D．x2＋2x－3＝0
6．一条排水管的截面如图所示，已知排水管的半径OB＝10，水面宽AB＝16，则截面圆心O到水面的距离OC是（ ）
A．4B．5C．6D．6
7．已知⊙O的半径为1,点P到圆心的距离为d，若关于x的方程x-2x+d=0有实数根,则点P ( )
A．在⊙O的内部B．在⊙O的外部C．在⊙O上D．在⊙O上或⊙O内部
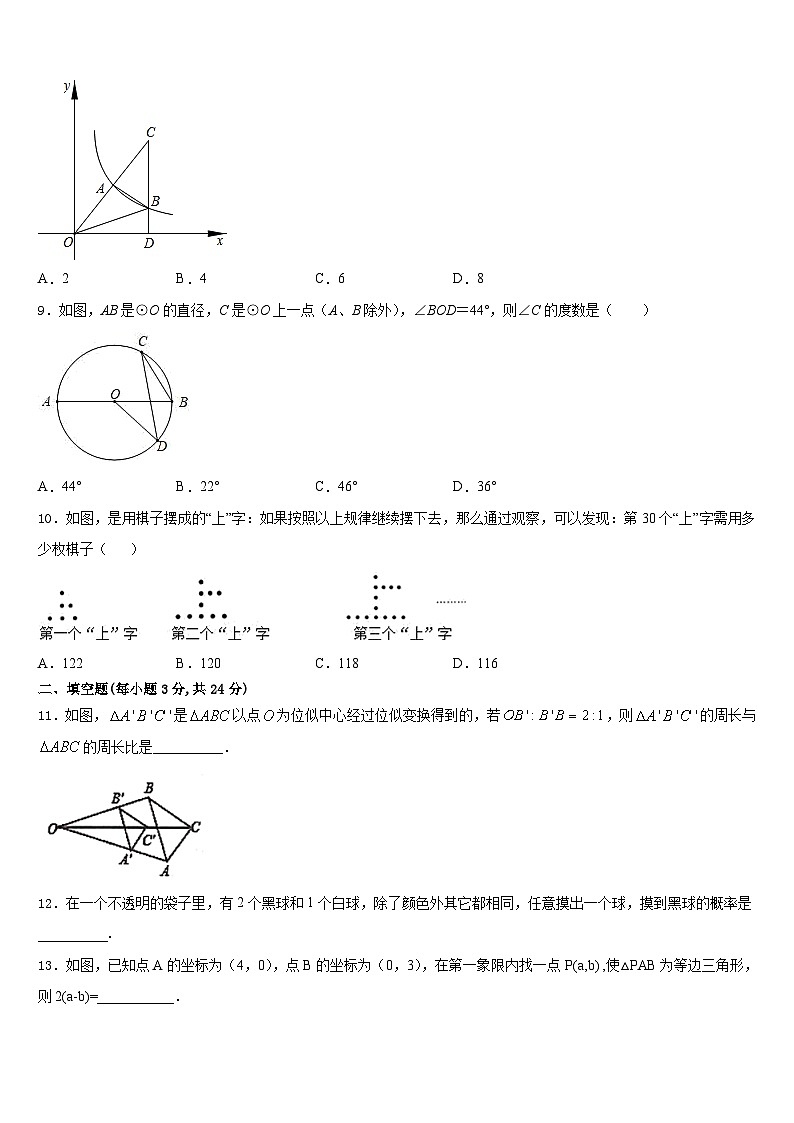
8．如图，CD⊥x轴，垂足为D，CO，CD分别交双曲线y＝于点A，B，若OA＝AC，△OCB的面积为6，则k的值为（ ）
A．2B．4C．6D．8
9．如图，AB是⊙O的直径，C是⊙O上一点（A、B除外），∠BOD＝44°，则∠C的度数是（ ）
A．44°B．22°C．46°D．36°
10．如图，是用棋子摆成的“上”字：如果按照以上规律继续摆下去，那么通过观察，可以发现：第30个“上”字需用多少枚棋子（ ）
A．122B．120C．118D．116
二、填空题(每小题3分,共24分)
11．如图，是以点为位似中心经过位似变换得到的，若，则的周长与的周长比是__________．
12．在一个不透明的袋子里，有2个黑球和1个白球，除了颜色外其它都相同，任意摸出一个球，摸到黑球的概率是__________．
13．如图，已知点A的坐标为（4，0），点B的坐标为（0，3），在第一象限内找一点P(a,b) ,使△PAB为等边三角形，则2(a-b)=___________．
14．如图，已知△ABC，D，E分别在AB，AC边上，且DE∥BC，AD＝2，DB＝3，△ADE面积是4，则四边形DBCE的面积是_____．
15．设、是关于的方程的两个根，则__________．
16．如图，内接于， 则的半径为__________．
17．甲、乙两人在100米短跑训练中，某5次的平均成绩相等，甲的方差是0.12，乙的方差是0.05，这5次短跑训练成绩较稳定的是_____．（填“甲”或“乙”）
18．比较大小：________．（填“，或”）
三、解答题(共66分)
19．（10分）用适当的方法解方程：
（1）x2+2x=0
（2）x2﹣4x+1=0
20．（6分）某校要求九年级同学在课外活动中，必须在五项球类（篮球、足球、排球、羽毛球、乒乓球）活动中任选一项（只能选一项）参加训练，为了了解九年级学生参加球类活动的整体情况，现以九年级2班作为样本，对该班学生参加球类活动的情况进行统计，并绘制了如图所示的不完整统计表和扇形统计图：
根据图中提供的信息，解答下列问题：
（1）a＝ ，b＝ ；
（2）该校九年级学生共有600人，则该年级参加足球活动的人数约 人；
（3）该班参加乒乓球活动的4位同学中，有2位男同学（A，B）和2位女同学（C，D），现准备从中选取两名同学组成双打组合，用树状图或列表法求恰好选出一男一女组成混合双打组合的概率．
21．（6分）如图，在平面直角坐标系中，的顶点坐标分别为， ，．
（1）的面积是_______；
（2）请以原点为位似中心，画出，使它与的相似比为，变换后点的对应点分别为点，点在第一象限；
（3）若为线段上的任一点，则变换后点的对应点的坐标为 _______．
22．（8分）如图所示，在Rt△ABC中，点O在斜边AB上，以O为圆心，OB为半径作圆O，分别与BC、AB相交于点D、E，连接AD，已知∠CAD＝∠B．
（1）求证：AD是⊙O的切线；
（2）若∠B＝30°，CD＝，求劣弧BD的长；
（3）若AC＝2，BD＝3，求AE的长．
23．（8分）如图，在平面直角坐标系中，直线交轴于点，交轴于点，点是射线上一动点（点不与点，重合），过点作垂直于轴，交直线于点，以直线为对称轴，将翻折，点的对称点落在轴上，以，为邻边作平行四边形．设点，与重叠部分的面积为．
（1）的长是__________，的长是___________（用含的式子表示）；
（2）求关于的函数关系式，并写出自变量的取值范围．
24．（8分）永祚寺双塔，又名凌霄双塔，是山西省会太原现存古建筑中最高的建筑. 位于太原市城区东南向山脚畔.数学活动小组的同学对其中一塔进行了测量.测量方 法如下：如图所示，间接测得该塔底部点到地面上一点的距离为，塔的顶端 为点，且，在点处竖直放一根标杆，其顶端为，在的延长 线上找一点，使三点在同一直线上，测得．
（1）方法 1，已知标杆，求该塔的高度；
（2）方法 2，测得，已知，求该塔的高度.
25．（10分）某校3男2女共5名学生参加黄石市教育局举办的“我爱黄石”演讲比赛．
（1）若从5名学生中任意抽取3名，共有多少种不同的抽法，列出所有可能情形；
（2）若抽取的3名学生中，某男生抽中，且必有1女生的概率是多少？
26．（10分）在如图所示的网格图中，已知和点
（1）在网格图中点M为位似中心，画出，使其与的位似比为1：1．
（1）写出的各顶点的坐标．
参考答案
一、选择题(每小题3分,共30分)
1、D
2、B
3、C
4、D
5、D
6、D
7、D
8、B
9、B
10、A
二、填空题(每小题3分,共24分)
11、2：1
12、
13、
14、1
15、1
16、2
17、乙
18、<
三、解答题(共66分)
19、（1）x1=0，x2=﹣2；（2）x1=2，x2=2．
20、（1）16，20；（2）90；（3）
21、（1）12；（2）见解析；（3）．
22、（1）见解析；（2）；（3）AE＝
23、（1），；（2）
24、（1）55m；（2）54.5m
25、（1）共有10种不同的抽法，分别是：男男男，男男女，男男女，男男女，男男女，男女女，男男女，男男女，男女女，男女女；（2）
26、（1）图见解析；（1）．
九年级2班参加球类活动人数统计表
项目
篮球
足球
乒乓球
排球
羽毛球
人数
a
6
4
8
6