湖北省黄冈市红安二中学2023-2024学年数学九年级第一学期期末复习检测模拟试题含答案

这是一份湖北省黄冈市红安二中学2023-2024学年数学九年级第一学期期末复习检测模拟试题含答案，共7页。
学校_______ 年级_______ 姓名_______
注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1．如图，△A′B′C′是△ABC以点O为位似中心经过位似变换得到的，若△A′B′C′的面积与△ABC的面积比是4：9，则OB′：OB为（ ）
A．2：3B．3：2C．4：5D．4：9
2．一元二次方程x2+x+1＝0的根的情况是（ ）．
A．有两个不相等的实数根B．有两个相等的实数根
C．没有实数根D．以上说法都不对
3．点M(a，2a)在反比例函数y＝的图象上，那么a的值是( )
A．4B．﹣4C．2D．±2
4．如图，在△ABC中，点D在BC上，DE∥AC，DF∥AB，下列四个判断中不正确的是( )
A．四边形AEDF是平行四边形
B．若∠BAC＝90°，则四边形AEDF是矩形
C．若AD平分∠BAC，则四边形AEDF是矩形
D．若AD⊥BC且AB＝AC，则四边形AEDF是菱形
5．用频率估计概率，可以发现，某种幼树在一定条件下移植成活的概率为0.9，下列说法正确的是（ ）
A．种植10棵幼树，结果一定是“有9棵幼树成活”
B．种植100棵幼树，结果一定是“90棵幼树成活”和“10棵幼树不成活”
C．种植10n棵幼树，恰好有“n棵幼树不成活”
D．种植n棵幼树，当n越来越大时，种植成活幼树的频率会越来越稳定于0.9
6．下列图形中，不是中心对称图形的是（ ）
A．B．C．D．
7．一次抽奖活动特等奖的中奖率为,把用科学记数法表示为（ ）
A．B．C．D．
8．在双曲线的每一分支上，y都随x的增大而增大，则k的值可以是（ ）
A．2B．3C．0D．1
9．一个不透明的袋中装有2个红球和4个黄球，这些球除颜色外完全相同．从袋中随机摸出一个球，摸到黄球的概率是（ ）
A．B．C．D．
10．如图，矩形纸片ABCD中，AB=4，AD=3，折叠纸片使AD边落在对角线 BD上，点A落在点A' 处，折痕为DG，求AG的长为（ ）
A．1.5B．2C．2.5D．3
二、填空题(每小题3分,共24分)
11．抛物线的部分图象如图所示，对称轴是直线，则关于的一元二次方程的解为____．
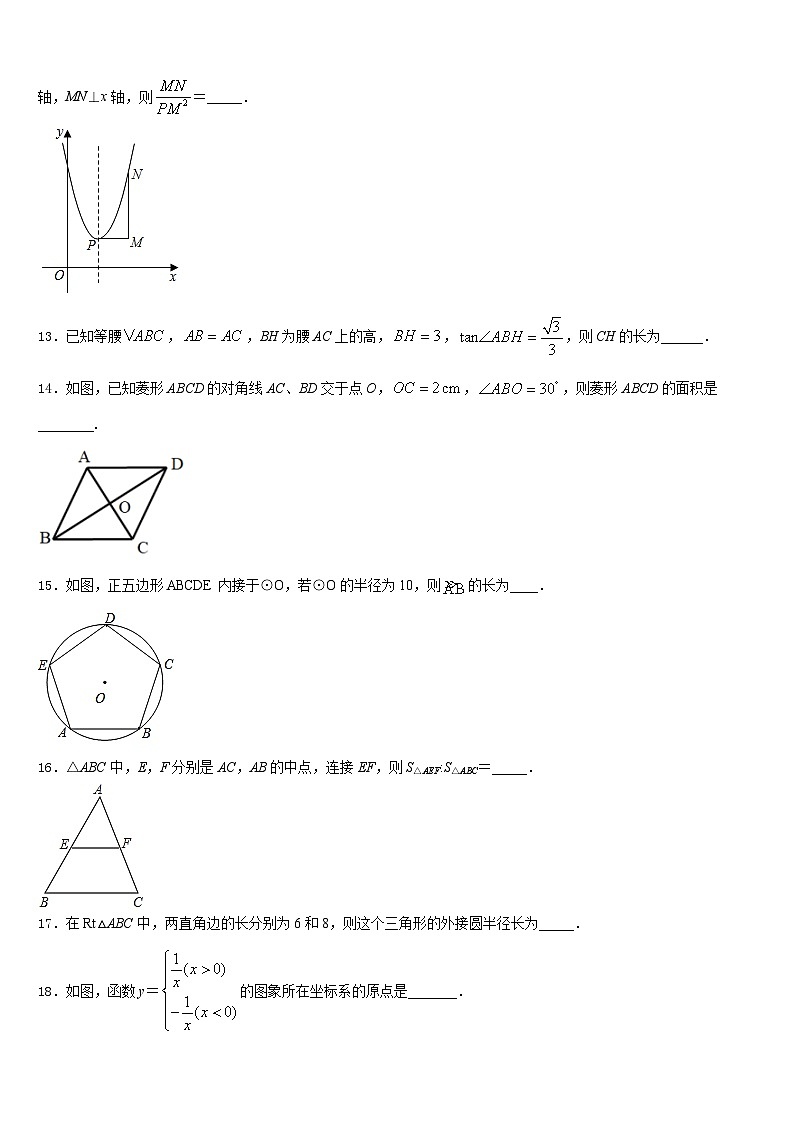
12．二次函数y＝2x2﹣4x+4的图象如图所示，其对称轴与它的图象交于点P，点N是其图象上异于点P的一点，若PM⊥y轴，MN⊥x轴，则＝_____．
13．已知等腰，，BH为腰AC上的高，，，则CH的长为______．
14．如图，已知菱形ABCD的对角线AC、BD交于点O，，，则菱形ABCD的面积是________.
15．如图，正五边形ABCDE内接于⊙O，若⊙O的半径为10，则的长为____．
16．△ABC中，E，F分别是AC，AB的中点，连接EF，则S△AEF:S△ABC＝_____．
17．在Rt△ABC中，两直角边的长分别为6和8，则这个三角形的外接圆半径长为_____．
18．如图，函数y＝的图象所在坐标系的原点是_______．
三、解答题(共66分)
19．（10分）瑞安市曹村镇“八百年灯会”成为温州“申遗”的宝贵项目．某公司生产了一种纪念花灯，每件纪念花灯制造成本为18元．设销售单价x（元），每日销售量y（件）每日的利润w（元）．在试销过程中，每日销售量y（件）、每日的利润w（元）与销售单价x（元）之间存在一定的关系，其几组对应量如下表所示：
（1）根据表中数据的规律，分别写出毎日销售量y（件），每日的利润w（元）关于销售单价x（元）之间的函数表达式．（利润＝（销售单价﹣成本单价）×销售件数）．
（2）当销售单价为多少元时，公司每日能够获得最大利润？最大利润是多少？
（3）根据物价局规定，这种纪念品的销售单价不得高于32元，如果公司要获得每日不低于350元的利润，那么制造这种纪念花灯每日的最低制造成本需要多少元？
20．（6分）在面积都相等的一组三角形中，当其中一个三角形的一边长为1时，这条边上的高为1．
（1）①求关于的函数解析式；
②当时，求的取值范围；
（2）小明说其中有一个三角形的一边与这边上的高之和为4，你认为小明的说法正确吗？为什么？
21．（6分）已知关于的一元二次方程.
（1） 求证：对于任意实数，方程总有两个不相等的实数根；
（2）若方程的一个根是1，求的值及方程的另一个根.
22．（8分）已知a＝，b＝，求．
23．（8分）综合与实践
问题情境
数学课上，李老师提出了这样一个问题：如图1，点是正方形内一点，，，.你能求出的度数吗？
(1)小敏与同桌小聪通过观察、思考、讨论后，得出了如下思路：
思路一：将绕点逆时针旋转，得到，连接，求出的度数.
思路二：将绕点顺时针旋转，得到，连接，求出的度数.
请参考以上思路，任选一种写出完整的解答过程.
类比探究
(2)如图2，若点是正方形外一点，，，，求的度数.
拓展应用
(3)如图3，在边长为的等边三角形内有一点，，，则的面积是______.
24．（8分）解方程：x2+4x﹣3＝1．
25．（10分）如图，在梯形ABCD中，AD//BC，AC与BD相交于点O，点E在线段OB上，AE的延长线与BC相交于点F，OD2 = OB·OE．
（1）求证：四边形AFCD是平行四边形；
（2）如果BC=BD，AE·AF=AD·BF，求证：△ABE∽△ACD．
26．（10分）已知和是关于的一元二次方程的两个不同的实数根．
（1）求的取值范围；
（2）如果且为整数，求的值．
参考答案
一、选择题(每小题3分,共30分)
1、A
2、C
3、D
4、C
5、D
6、A
7、D
8、C
9、B
10、A
二、填空题(每小题3分,共24分)
11、
12、1．
13、或
14、
15、2π
16、
17、1
18、M
三、解答题(共66分)
19、（1）y＝﹣2x+100，w＝﹣2x2+136x﹣1800；（2）当销售单价为34元时，每日能获得最大利润，最大利润是1元；（3）制造这种纪念花灯每日的最低制造成本需要648元．
20、（1）①；②；（2）小明的说法不正确．
21、（1）见解析；（2），
22、1．
23、 (1)∠APB=135°，(2)∠APB=45°；(3).
24、x1＝﹣2+, x2＝﹣2﹣
25、（1）证明见解析；（2）证明见解析
26、（1）；（2）－2
（元）
19
20
21
30
（件）
62
60
58
40