黑龙江省哈尔滨市光华中学2023-2024学年数学九上期末质量跟踪监视模拟试题含答案

这是一份黑龙江省哈尔滨市光华中学2023-2024学年数学九上期末质量跟踪监视模拟试题含答案，共8页。试卷主要包含了若. 则下列式子正确的是等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1．从数据，﹣6，1.2，π，中任取一数，则该数为无理数的概率为（ ）
A．B．C．D．
2．某学校要种植一块面积为200m2的长方形草坪，要求两边长均不小于10m，则草坪的一边长y（单位：m）随另一边长x（单位：m）的变化而变化的图象可能是（ ）
A．B．C．D．
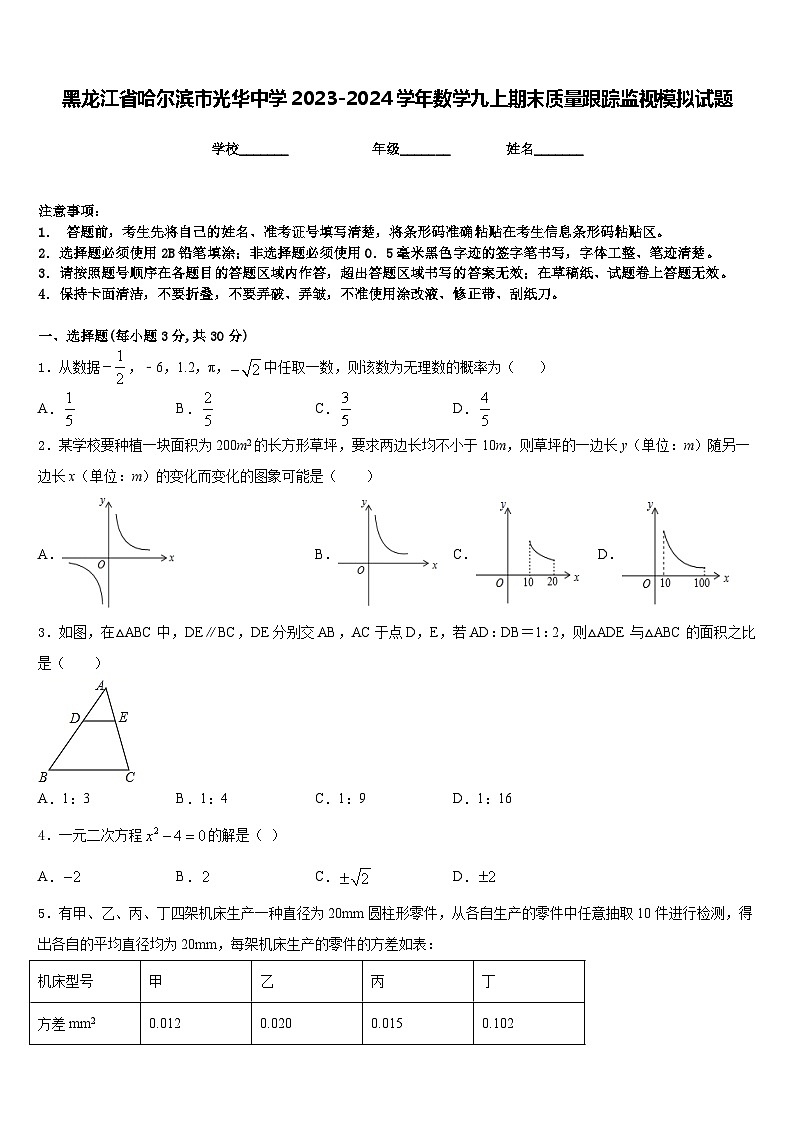
3．如图，在△ABC中，DE∥BC，DE分别交AB，AC于点D，E，若AD：DB＝1：2，则△ADE与△ABC的面积之比是（ ）
A．1：3B．1：4C．1：9D．1：16
4．一元二次方程的解是（ ）
A．B．C．D．
5．有甲、乙、丙、丁四架机床生产一种直径为20mm圆柱形零件，从各自生产的零件中任意抽取10件进行检测，得出各自的平均直径均为20mm，每架机床生产的零件的方差如表：
则在这四台机床中生产的零件最稳定的是（ ）．
A．甲B．乙C．丙D．丁
6．有一个矩形苗圃园，其中一边靠墙，另外三边用长为的篱笆围成．已知墙长为若平行于墙的一边长不小于则这个苗圃园面积的最大值和最小值分别为（ ）
A．B．
C．D．
7．若. 则下列式子正确的是（ ）
A．B．C．D．
8．如图，在中，是的中点，，，则的长为（ ）
A．B．4C．D．
9．甲、乙、丙三人站成一排拍照，则甲站在中间的概率是（ ）
A．B．C．D．
10．下列函数中，变量是的反比例函数是（ ）
A．B．C．D．
二、填空题(每小题3分,共24分)
11．已知，则___________.
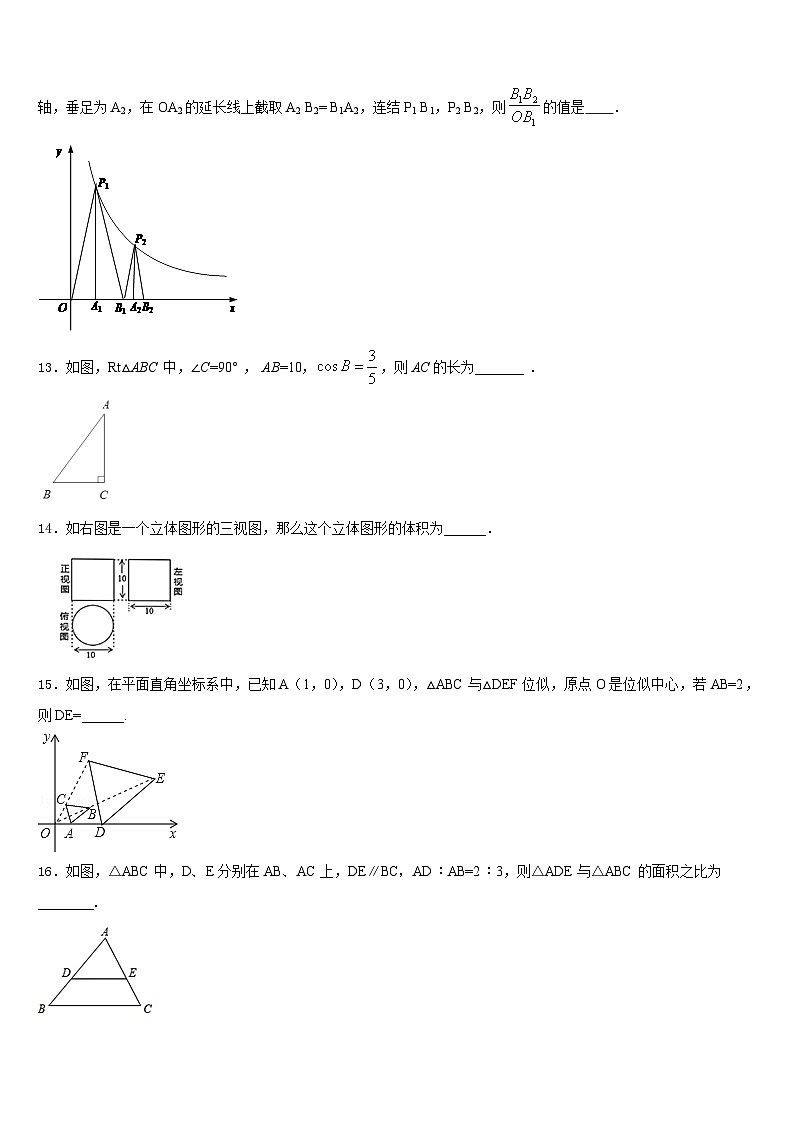
12．如图，在反比例函数位于第一象限内的图象上取一点P1，连结OP1，作P1A1⊥x轴，垂足为A1，在OA1的延长线上截取A1 B1= OA1，过B1作OP1的平行线，交反比例函数的图象于P2，过P2作P2A2⊥x轴，垂足为A2，在OA2的延长线上截取A2 B2= B1A2，连结P1 B1，P2 B2，则的值是 ．
13．如图，Rt△ABC 中，∠C=90° ， AB=10，，则AC的长为_______ .
14．如右图是一个立体图形的三视图，那么这个立体图形的体积为______．
15．如图，在平面直角坐标系中，已知A（1，0），D（3，0），△ABC与△DEF位似，原点O是位似中心，若AB=2，则DE=______.
16．如图，△ABC中，D、E分别在AB、AC上，DE∥BC，AD：AB=2：3，则△ADE与△ABC的面积之比为________．
17．在Rt△ABC 中，∠C是直角，sinA=，则csB=__________
18．如图，在等腰直角△ABC中，∠C＝90°，将△ABC绕顶点A逆时针旋转80°后得到△AB′C′，则∠CAB′的度数为_____．
三、解答题(共66分)
19．（10分）在一个不透明的盒子里装有三个标记为1，2，3的小球（材质、形状、大小等完全相同），甲先从中随机取出一个小球，记下数字为后放回，同样的乙也从中随机取出一个小球，记下数字为，这样确定了点的坐标．
（1）请用列表或画树状图的方法写出点所有可能的坐标；
（2）求点在函数的图象上的概率．
20．（6分）如图，在大楼AB的正前方有一斜坡CD，CD=13米，坡比DE:EC=1：，高为DE，在斜坡下的点C处测得楼顶B的仰角为64°，在斜坡上的点D处测得楼顶B的仰角为45°，其中A、C、E在同一直线上．
（1）求斜坡CD的高度DE；
（2）求大楼AB的高度；（参考数据：sin64°≈0.9，tan64°≈2）．
21．（6分）数学兴趣小组想利用所学的知识了解某广告牌的高度，已知CD＝2m．经测量，得到其它数据如图所示．其中∠CAH＝37°，∠DBH＝67°，AB＝10m，请你根据以上数据计算GH的长．（参考数据，，）
22．（8分）如图，AB是半圆O的直径，AD为弦，∠DBC=∠A．
（1）求证：BC是半圆O的切线；
（2）若OC∥AD，OC交BD于E，BD=6，CE=4，求AD的长．
23．（8分）已知是一张直角三角形纸片，其中，，小亮将它绕点逆时针旋转后得到，交直线于点.
（1）如图1，当时，所在直线与线段有怎样的位置关系？请说明理由.
（2）如图2，当，求为等腰三角形时的度数.
24．（8分）如图，在地面上竖直安装着AB、CD、EF三根立柱，在同一时刻同一光源下立柱AB、CD形成的影子为BG与DH.
（1）填空：判断此光源下形成的投影是： 投影.
（2）作出立柱EF在此光源下所形成的影子.
25．（10分）某中学举行“中国梦，我的梦”的演讲比赛，赛后整理参赛学生的成绩，将学生的成绩分为A、B、C、D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整，请你根据统计图解答下列问题.
（1）参加比赛的学生共有 名，在扇形统计图中，表示“D等级”的扇形的圆心角为 度，图中m的值为 ；
（2）补全条形统计图；
（3）组委会决定分别从本次比赛中获利A、B两个等级的学生中，各选出1名学生培训后搭档去参加市中学生演讲比赛，已知甲的等级为A，乙的等级为B，求同时选中甲和乙的概率.
26．（10分）如图，顶点为M的抛物线y=a(x+1)2-4分别与x轴相交于点A，B(点A在点B的)右侧)，与y轴相交于点C(0，﹣3)．
(1)求抛物线的函数表达式；
(2)判断△BCM是否为直角三角形，并说明理由．
(3)抛物线上是否存在点N(不与点C重合)，使得以点A，B，N为顶点的三角形的面积与S△ABC的面积相等？若存在，求出点N的坐标；若不存在，请说明理由．
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、C
4、D
5、A
6、C
7、A
8、D
9、B
10、B
二、填空题(每小题3分,共24分)
11、
12、
13、8
14、250π
15、1
16、4：1
17、
18、125°
三、解答题(共66分)
19、（1）见解析；（2）．
20、（1）斜坡CD的高度DE是5米；（2）大楼AB的高度是34米．
21、GH的长为10m
22、（1）见解析；（2）AD=4.5.
23、（1）BD与FM互相垂直，理由见解析；（2）β的度数为30°或75°或120°．
24、（1）中心；（2）如图，线段FI为此光源下所形成的影子. 见解析
25、（1）20，72，1;（2）见解析；（3）
26、 (1)；(2)见解析；(3)存在，(，3)，(，3)，(，)
机床型号
甲
乙
丙
丁
方差mm2
0.012
0.020
0.015
0.102