2023-2024学年山东省济南市市中学区五校联考数学九年级第一学期期末达标检测模拟试题含答案

这是一份2023-2024学年山东省济南市市中学区五校联考数学九年级第一学期期末达标检测模拟试题含答案，共9页。试卷主要包含了考生要认真填写考场号和座位序号等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。
一、选择题（每题4分，共48分）
1．一个袋子中装有6个黑球3个白球，这些球除颜色外，形状、大小、质地等完全相同，在看不到球的条件下，随机地从这个袋子中摸出一个球，摸到白球的概率为（ ）
A．B．C．D．
2．如图，将绕点A按顺时针旋转一定角度得到，点B的对应点D恰好落在BC边上.若，则CD的长为（ ）
A．1B．C．D．2
3．如图，在Rt△ABC中，∠C=Rt∠，则csA可表示为（ ）
A．B．C．D．
4．在皮影戏的表演中，要使银幕上的投影放大，下列做法中正确的是（ ）
A．把投影灯向银幕的相反方向移动B．把剪影向投影灯方向移动
C．把剪影向银幕方向移动D．把银幕向投影灯方向移动
5．点A(﹣3，2)关于x轴的对称点A′的坐标为（ ）
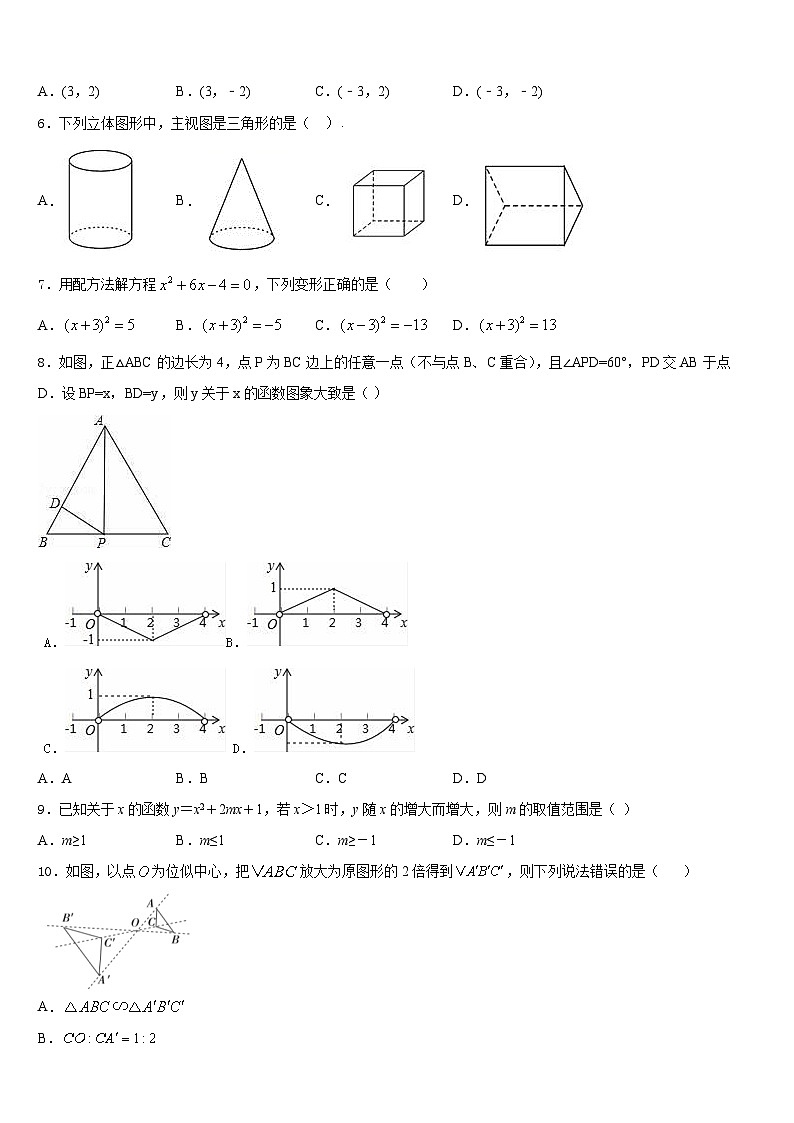
A．(3，2)B．(3，﹣2)C．(﹣3，2)D．(﹣3，﹣2)
6．下列立体图形中，主视图是三角形的是（ ）.
A．B．C．D．
7．用配方法解方程，下列变形正确的是（ ）
A．B．C．D．
8．如图，正△ABC的边长为4，点P为BC边上的任意一点（不与点B、C重合），且∠APD=60°，PD交AB于点D．设BP=x，BD=y，则y关于x的函数图象大致是（ ）
A．AB．BC．CD．D
9．已知关于x的函数y＝x2＋2mx＋1，若x＞1时，y随x的增大而增大，则m的取值范围是（ ）
A．m≥1B．m≤1C．m≥－1D．m≤－1
10．如图，以点为位似中心，把放大为原图形的2倍得到，则下列说法错误的是（ ）
A．
B．
C．，，三点在同一直线上
D．
11．如图，已知一个直角三角板的直角顶点与原点重合，另两个顶点A，B的坐标分别为（-1，0），（0， ）．现将该三角板向右平移使点A与点O重合，得到△OCB’，则点B的对应点B’的坐标是（ ）
A．（1，0）B．（，）C．（1，）D．（-1，）
12．如图，菱形ABCD中，∠A＝60°，边AB＝8，E为边DA的中点，P为边CD上的一点，连接PE、PB，当PE＝EB时，线段PE的长为（ ）
A．4B．8C．4D．4
二、填空题（每题4分，共24分）
13．若二次函数y＝2（x+1）2+3的图象上有三个不同的点A（x1，4）、B（x1+x2，n）、C（x2，4），则n的值为_____．
14．在△ABC中，若∠A＝30°，∠B＝45°，AC＝，则BC＝_______.
15．如图，把置于平面直角坐标系中，点A的坐标为，点B的坐标为，点P是内切圆的圆心．将沿x轴的正方向作无滑动滚动，使它的三边依次与x轴重合，第一次滚动后圆心为，第二次滚动后圆心为，…，依此规律，第2019次滚动后，内切圆的圆心的坐标是________．
16．抛物线y=3（x﹣2）2+5的顶点坐标是_____．
17．如图，⊙的半径于点，连接并延长交⊙于点，连接.若,则的长为 ___ .
18．一组数据：2,5,3,1,6，则这组数据的中位数是________.
三、解答题（共78分）
19．（8分）如图，已知直线与轴交于点，与轴交于点，抛物线经过、两点并与轴的另一个交点为，且.
（1）求抛物线的解析式；
（2）点为直线上方对称轴右侧抛物线上一点，当的面积为时，求点的坐标；
（3）在（2）的条件下，连接，作轴于，连接、，点为线段上一点，点为线段上一点，满足，过点作交轴于点，连接，当时，求的长.
20．（8分）如图是某区域的平面示意图，码头A在观测站B的正东方向，码头A的北偏西方向上有一小岛C，小岛C在观测站B的北偏西方向上，码头A到小岛C的距离AC为10海里．
（1）填空： 度， 度；
（2）求观测站B到AC的距离BP（结果保留根号）．
21．（8分）如图，已知直线与两坐标轴分别交于A、B两点，抛物线 经过点A、B，点P为直线AB上的一个动点，过P作y轴的平行线与抛物线交于C点, 抛物线与x轴另一个交点为D．
（1）求图中抛物线的解析式；
（2）当点P在线段AB上运动时，求线段PC的长度的最大值；
（3）在直线AB上是否存在点P，使得以O、A、P、C为顶点的四边形是平行四边形？若存在，请求出此时点P 的坐标，若不存在，请说明理由．
22．（10分）如图，四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90°，E为AB的中点，
（1）求证：AC2=AB•AD；
（2）求证：CE∥AD；
（3）若AD=4，AB=6，求的值．
23．（10分）某报社为了解市民对“社会主义核心价值观”的知晓程度，采取随机抽样的方式进行问卷调查，调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”三个等级，并根据调查结果绘制了如下两幅不完整的统计图．
(1)这次调查的市民人数为________人，m＝________，n＝________；
(2)补全条形统计图；
(3)若该市约有市民100000人，请你根据抽样调查的结果，估计该市大约有多少人对“社会主义核心价值观”达到“A.非常了解”的程度．
24．（10分）鄂州某个体商户购进某种电子产品的进价是50元/个，根据市场调研发现售价是80元/个时，每周可卖出160个，若销售单价每个降低2元，则每周可多卖出20个．设销售价格每个降低x元（x为偶数），每周销售量为y个．
（1）直接写出销售量y个与降价x元之间的函数关系式；
（2）设商户每周获得的利润为W元，当销售单价定为多少元时，每周销售利润最大，最大利润是多少元？
25．（12分）在平面直角坐标系中，已知P（,）,R（,）两点，且，，若过点P作轴的平行线，过点R作轴的平行线，两平行线交于一点S，连接PR，则称△PRS为点P，R，S的“坐标轴三角形”.若过点R作轴的平行线，过点P作轴的平行线，两平行线交于一点，连接PR，则称△RP为点R，P，的“坐标轴三角形”.右图为点P，R，S的“坐标轴三角形”的示意图.
（1）已知点A（0，4），点B（3，0）,若△ABC是点A，B，C的“坐标轴三角形”，则点C的坐标为 ；
（2）已知点D（2，1），点E（e，4），若点D，E，F的“坐标轴三角形”的面积为3，求e的值.
（3）若的半径为，点M（，4），若在上存在一点N，使得点N，M，G的“坐标轴三角形”为等腰三角形，求的取值范围.
26．（12分）探究题：如图1，和均为等边三角形，点在边上，连接．
（1）请你解答以下问题：
①求的度数；
②写出线段，，之间数量关系，并说明理由．
（2）拓展探究：如图2，和均为等腰直角三角形，，点在边上，连接．请判断的度数及线段，，之间的数量关系，并说明理由．
（3）解决问题：如图3，在四边形中，，，，与交于点．若恰好平分，请直接写出线段的长度．
参考答案
一、选择题（每题4分，共48分）
1、B
2、D
3、C
4、B
5、D
6、B
7、D
8、C
9、C
10、B
11、C
12、D
二、填空题（每题4分，共24分）
13、1
14、
15、
16、（2，5）．
17、
18、3
三、解答题（共78分）
19、（3）；（3）R（3，3）；（3）3或．
20、（1）30，45；（2）（5－5）海里
21、（1）；（2）当时，线段PC有最大值是2；（3），，
22、（1）见解析
（2）见解析
（1）．
23、 (1)500，12，32；(2)补图见解析；(3)该市大约有32000人对“社会主义核心价值观”达到“A.非常了解”的程度．
24、（1）；（2）当销售单价定为74元或72元时，每周销售利润最大，最大利润是5280元；
25、（1）（3，4）；（2）或；（3）m的取值范围是或.
26、（1）①；②线段、、之间的数量关系为：，理由见解析；
（2），，理由见解析．
（3）理由见解析．