2023-2024学年山东省枣庄数学九年级第一学期期末质量跟踪监视模拟试题含答案

这是一份2023-2024学年山东省枣庄数学九年级第一学期期末质量跟踪监视模拟试题含答案，共8页。试卷主要包含了抛物线y=的对称轴方程为等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项
1．考试结束后，请将本试卷和答题卡一并交回．
2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．
3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．
4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．
5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．
一、选择题（每题4分，共48分）
1．在一个不透明的盒子里有2个红球和n个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个，摸到红球的概率是，则n的值为（ ）
A．3B．5C．8D．10
2．如图，点A，B，C都在⊙O上，若∠C=30°，则∠AOB的度数为（ ）
A．30°B．60°C．150°D．120°
3．反比例函数y=的图象经过点（3，﹣2），下列各点在图象上的是（ ）
A．（﹣3，﹣2）B．（3，2）C．（﹣2，﹣3）D．（﹣2，3）
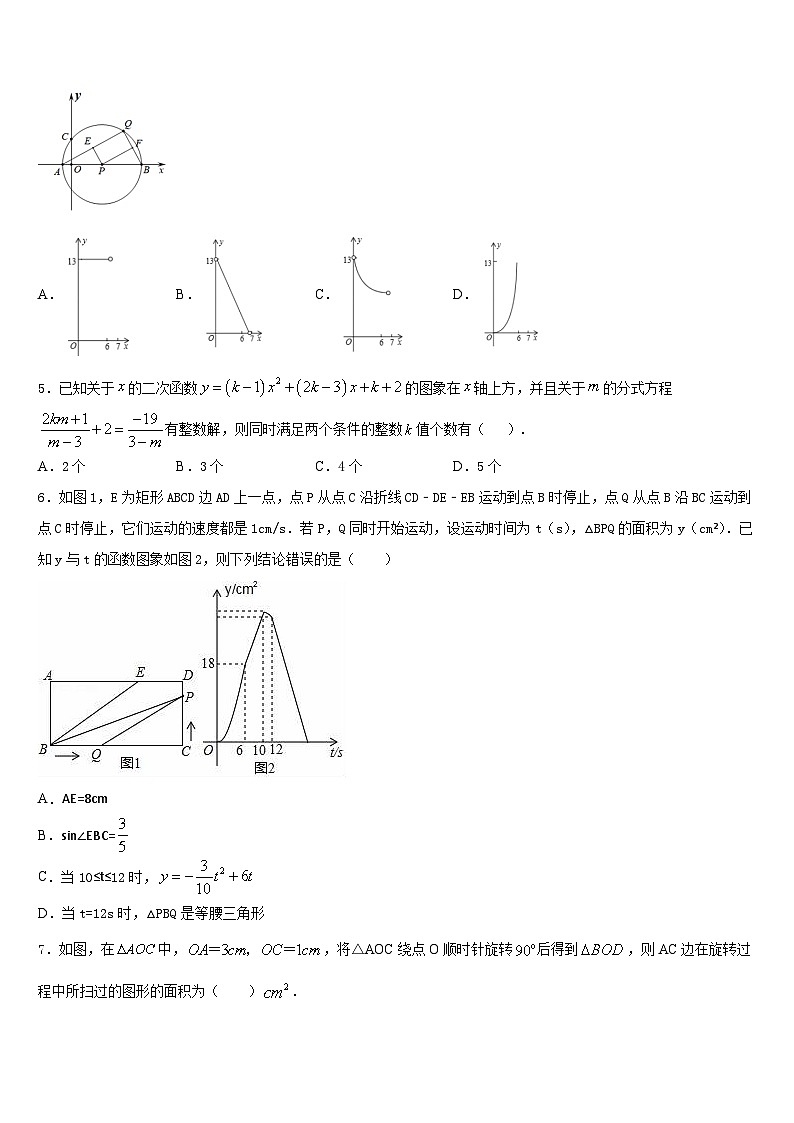
4．如图，在平面直角坐标系中，以为圆心作⊙，⊙与轴交于、，与轴交于点，为⊙上不同于、的任意一点，连接、，过点分别作于，于．设点的横坐标为，．当点在⊙上顺时针从点运动到点的过程中，下列图象中能表示与的函数关系的部分图象是（ ）
A．B．C．D．
5．已知关于的二次函数的图象在轴上方，并且关于的分式方程有整数解，则同时满足两个条件的整数值个数有（ ）.
A．2个B．3个C．4个D．5个
6．如图1，E为矩形ABCD边AD上一点，点P从点C沿折线CD﹣DE﹣EB运动到点B时停止，点Q从点B沿BC运动到点C时停止，它们运动的速度都是1cm/s．若P，Q同时开始运动，设运动时间为t（s），△BPQ的面积为y（cm2）．已知y与t的函数图象如图2，则下列结论错误的是（ ）
A．AE=8cm
B．sin∠EBC=
C．当10≤t≤12时，
D．当t=12s时，△PBQ是等腰三角形
7．如图，在中，，将△AOC绕点O顺时针旋转后得到，则AC边在旋转过程中所扫过的图形的面积为（ ）．
A．B．C．D．
8．通过对《一元二次方程》全章的学习，同学们掌握了一元二次方程的三种解法：配方法、公式法、因式分解法，其实，每种解法都是把一个一元二次方程转化为两个一元一次方程来解，体现的基本思想是（ ）
A．转化B．整体思想C．降次D．消元
9．抛物线y=(x－4)(x＋2)的对称轴方程为（ ）
A．直线x=-2B．直线x=1C．直线x=-4D．直线x=4
10．如图，点A、B、C都在上，若∠AOB＝72°，则∠ACB的度数为（）
A．18°B．30°C．36°D．72°
11．关于x的一元二次方程x2+bx-6=0的一个根为2，则b的值为( )
A．-2B．2C．-1D．1
12．如图，、、分别切于、、点，若圆的半径为6，，则的周长为（ ）
A．10B．12C．16D．20
二、填空题（每题4分，共24分）
13．从，0，π，3.14，6这五个数中随机抽取一个数，抽到有理数的概率是____．
14．时钟的时针不停地旋转，从上午时到上午时，时针旋转的旋转角是__________度．
15．如图，△ABC是等腰直角三角形，BC是斜边，P为△ABC内一点，将△ABP绕点A逆时针旋转后与△ACP′重合，若AP=1，那么线段PP′的长等于_____．
16．因式分解：_______________________．
17．墙壁CD上D处有一盏灯(如图)，小明站在A处测得他的影长与身长相等，都为1.6m，他向墙壁走1m到B处时发现影子刚好落在A点，则灯泡与地面的距离CD＝____．
18．在△ABC中，∠ABC=90°，已知AB=3，BC=4，点Q是线段AC上的一个动点，过点Q作AC的垂线交直线AB于点P，当△PQB为等腰三角形时，线段AP的长为_____．
三、解答题（共78分）
19．（8分）如图，已知正方形的边长为，点是对角线上一点，连接，将线段绕点顺时针旋转至的位置，连接、．
（1）求证：；
（2）当点在什么位置时，的面积最大？并说明理由．
20．（8分）一只不透明的袋子中，装有2个白球，1个红球，1个黄球，这些球除颜色外都相同．请用列表法或画树形图法求下列事件的概率：
(1)搅匀后从中任意摸出1个球，恰好是白球．
(2)搅匀后从中任意摸出2个球，2个都是白球．
(3)再放入几个除颜色外都相同的黑球，搅匀后从中任意摸出1个球，恰好是黑球的概率为，求放入了几个黑球？
21．（8分）某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查，调查的运动项目有：篮球、羽毛球、乒乓球、跳绳及其它项目（每位同学仅选一项）．根据调查结果绘制了如下不完整的频数分布表和扇形统计图：
请根据以上图表信息解答下列问题：
（1）频数分布表中的m=________，n=________；
（2）在扇形统计图中，“乒乓球”所在的扇形的圆心角的度数为________°；
（3）从选择“篮球”选项的60名学生中，随机抽取10名学生作为代表进行投篮测试，则其中某位学生被选中的概率是________．
22．（10分）若关于x的方程有两个相等的实数根
（1）求b的值；
（2）当b取正数时，求此时方程的根，
23．（10分）如图，AB、AD是⊙O的弦，△ABC是等腰直角三角形，△ADC≌△AEB，请仅用无刻度直尺作图：
(1)在图1中作出圆心O；
(2)在图2中过点B作BF∥AC．
24．（10分）如图，为正方形对角线上一点，以为圆心，长为半径的与相切于点.
（1）求证：与相切.
（2）若正方形的边长为1，求半径的长.
25．（12分）如图，在平面直角坐标系中，点的坐标为，点在第一象限，，点是上一点，，．
（1）求证：；
（2）求的值．
26．（12分）在的方格纸中，的三个顶点都在格点上．
在图1中画出线段BD，使，其中D是格点；
在图2中画出线段BE，使，其中E是格点．
参考答案
一、选择题（每题4分，共48分）
1、C
2、B
3、D
4、A
5、B
6、D
7、B
8、C
9、B
10、C
11、D
12、C
二、填空题（每题4分，共24分）
13、
14、
15、．
16、
17、m
18、或1．
三、解答题（共78分）
19、（1）见解析；（2）在中点时，的面积最大，见解析
20、（1）；（2）；（3）n＝1
21、2 0.3 108
22、（1）b=2或b=；（2）x1=x2=2；
23、见解析.
24、（1）见解析；（2）
25、（1）证明见解析；（2）cs∠ABO=
26、（1）画图见解析；（2）画图见解析.