2023-2024学年山西省运城数学九年级第一学期期末监测模拟试题含答案

这是一份2023-2024学年山西省运城数学九年级第一学期期末监测模拟试题含答案，共8页。试卷主要包含了若不等式组无解，则的取值范围为，关于二次函数，下列说法错误的是，若，，则的值为等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
请考生注意：
1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。
一、选择题（每题4分，共48分）
1．如图，矩形OABC的顶点A、C分别在x轴、y轴的正半轴上，点M是边BC上一动点（不与B、C重合）．过点M的双曲线（x>0）交AB于点N，连接OM、ON．下列结论：
①△OCM与△OAN的面积相等；
②矩形OABC的面积为2k；
③线段BM与BN的长度始终相等；
④若BM=CM，则有AN=BN．
其中一定正确的是（ ）
A．①④B．①②C．②④D．①③④
2．如图，在Rt△ABC中，∠BAC=90º，AH是高，AM是中线，那么在结论①∠B=∠BAM，②∠B=∠MAH，③∠B=∠CAH中错误的个数有（ ）
A．0个B．1个C．2个D．3个
3．一个三角形的两边长分别为和，第三边长是方程的根，则这个三角形的周长为（ ）
A．B．C．10或11D．不能确定
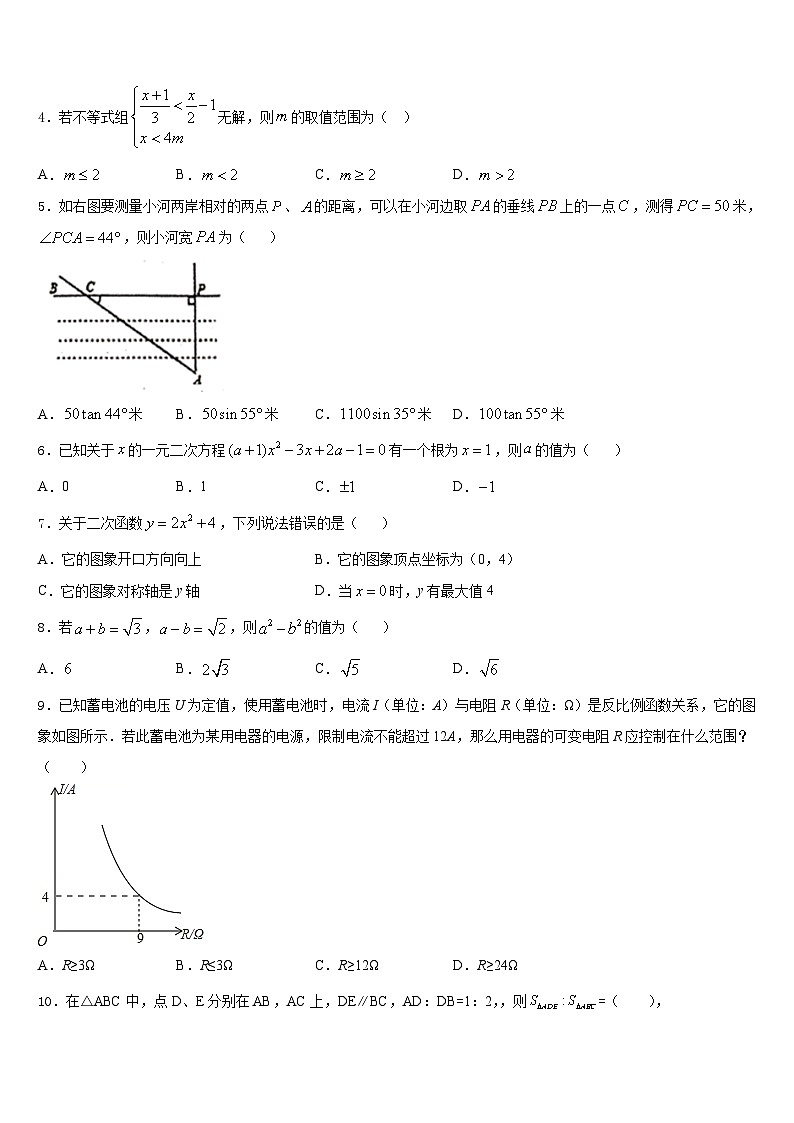
4．若不等式组无解，则的取值范围为（ ）
A．B．C．D．
5．如右图要测量小河两岸相对的两点、的距离，可以在小河边取的垂线上的一点，测得米，，则小河宽为（ ）
A．米B．米C．米D．米
6．已知关于的一元二次方程有一个根为，则的值为（ ）
A．0B．1C．D．
7．关于二次函数，下列说法错误的是（ ）
A．它的图象开口方向向上B．它的图象顶点坐标为（0，4）
C．它的图象对称轴是y轴D．当时，y有最大值4
8．若，，则的值为（ ）
A．B．C．D．
9．已知蓄电池的电压U为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示．若此蓄电池为某用电器的电源，限制电流不能超过12A，那么用电器的可变电阻R应控制在什么范围？（ ）
A．R≥3ΩB．R≤3ΩC．R≥12ΩD．R≥24Ω
10．在△ABC中，点D、E分别在AB，AC上，DE∥BC，AD：DB=1：2，，则=（ ），
A．B．C．D．
11．如图，△ABC内接于圆，D是BC上一点，将∠B沿AD翻折，B点正好落在圆点E处，若∠C＝50°，则∠BAE的度数是（ ）
A．40°B．50°C．80°D．90°
12．如图，在中，是直径，点是上一点，点是弧的中点，于点，过点的切线交的延长线于点，连接，分别交，于点．连接，关于下列结论：① ；②；③点是的外心，其中正确结论是（ ）
A．①②B．①③C．②③D．①②③
二、填空题（每题4分，共24分）
13．一个不透明的袋中装有若干个红球，为了估计袋中红球的个数，小文在袋中放入3个白球(每个球除颜色外其余都与红球相同).摇匀后每次随机从袋中摸出一个球，记下颜色后放回袋中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.7左右，则袋中红球约有_____个.
14．从，0，，，1.6中随机取一个数，取到无理数的概率是__________．
15．一个暗箱里放有a个除颜色外完全相同的球，这a个球中红球只有3个．若每次将球搅匀后，任意摸出1个球记下颜色再放回暗箱．通过大量重复摸球试验后发现，摸到红球的频率稳定在20%附近，那么可以推算出a的值大约是_______．
16．如图所示，在方格纸上建立的平面直角坐标系中，将绕点按顺时针方向旋转，得，则点的坐标为_________.
17．将二次函数y＝x2﹣6x+8化成y＝a（x+m）2+k的形式是_____．
18．一个口袋中有红球、白球共10个，这些球除色外都相同．将口袋中的球搅拌均匀，从中随机摸出一个球，记下它的颜色后再放回口袋中，不断重复这一过程，共摸了100次球，发现有60次摸到红球．请你估计这个口袋中有_____个白球．
三、解答题（共78分）
19．（8分）如图，点A是我市某小学，在位于学校南偏西15°方向距离120米的C点处有一消防车.某一时刻消防车突然接到报警电话，告知在位于C点北偏东75°方向的F点处突发火灾，消防队必须立即沿路线CF赶往救火．已知消防车的警报声传播半径为110米，问消防车的警报声对学校是否会造成影响？若会造成影响，已知消防车行驶的速度为每小时60千米，则对学校的影响时间为几秒？（≈3.6，结果精确到1秒）
20．（8分）已知在平面直角坐标系xOy中，抛物线（b为常数）的对称轴是直线x=1．
（1）求该抛物线的表达式；
（2）点A（8，m）在该抛物线上，它关于该抛物线对称轴对称的点为A'，求点A'的坐标；
（3）选取适当的数据填入下表，并在如图5所示的平面直角坐标系内描点，画出该抛物线．
21．（8分）如图，在平面直角坐标系中，的顶点坐标分别为A(2，6)，B(0，4)，C(3，3)．（正方形网格的每个小正方形的边长都是1个单位长度）
（1）平移后，点A的对应点A1的坐标为(6，6)，画出平移后的；
（2）画出绕点C 1旋转180°得到的；
（3）绕点P(_______)旋转180°可以得到，请连接AP、A2P，并求AP在旋转过程中所扫过的面积．
22．（10分）已知抛物线y=x2+bx+c的图像过A（﹣1，0）、B（3，0）两点．求抛物线的解析式和顶点坐标.
23．（10分）图1是一辆登高云梯消防车的实物图，图2是其工作示意图，起重臂AC是可伸缩的，其转动点A距离地面BD的高度AE为3.5m．当AC长度为9m，张角∠CAE为112°时，求云梯消防车最高点C距离地面的高度CF．（结果精确到0.1m，参考数据：sin22°≈0.37，cs22°≈0.93，tan22°≈0.1．）
24．（10分）如图，是⊙的直径，是的中点，弦于点，过点作交的延长线于点．
（1）连接，求；
（2）点在上，，DF交于点．若，求的长．
25．（12分）定义：有两个相邻内角和等于另两个内角和的一半的四边形称为半四边形，这两个角的夹边称为对半线.
（1）如图1，在对半四边形中，，求与的度数之和；
（2）如图2，为锐角的外心，过点的直线交，于点，，，求证：四边形是对半四边形；
（3）如图3，在中，，分别是，上一点，，，为的中点，，当为对半四边形的对半线时，求的长.
26．（12分）解方程：3x（1x+1）=4x+1．
参考答案
一、选择题（每题4分，共48分）
1、A
2、B
3、B
4、A
5、A
6、B
7、D
8、D
9、A
10、A
11、C
12、C
二、填空题（每题4分，共24分）
13、1
14、
15、15个．
16、
17、y＝（x﹣3）2﹣1
18、1
三、解答题（共78分）
19、4秒
20、（1）；（2）（-6，49）；（3）答案见解析.
21、（1）图见解析；（2）图见解析；（3），AP所扫过的面积为．
22、y=x2-2x-3，顶点坐标为（1，-4）.
23、CF≈6.8m．
24、（1）；（2）．
25、（1）；（2）详见解析；（3）5.25.
26、=,= −．