陕西省岐山县联考2023-2024学年九上数学期末学业水平测试模拟试题含答案

这是一份陕西省岐山县联考2023-2024学年九上数学期末学业水平测试模拟试题含答案，共9页。试卷主要包含了答题时请按要求用笔等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1．如图，在矩形COED中，点D的坐标是(1，3)，则CE的长是（ ）
A．3B．C．D．4
2．如图，以点O为位似中心，将△ABC放大得到△DEF，若AD＝OA，则△ABC与△DEF 的面积之比为 ( )
A．1:2B．1:4C．1:5D．1:6
3．一个不透明的口袋中放着若干个红球和白球，这两种球除了颜色以外没有任何其他区别，袋中的球已经搅匀，从口袋中随机取出一个球，取出红球的概率是．如果袋中共有32个小球，那么袋中的红球有（ ）
A．4个B．6个C．8个D．10个
4．如图，边长都为4的正方形ABCD和正三角形EFG如图放置，AB与EF在一条直线上，点A与点F重合．现将△EFG沿AB方向以每秒1个单位的速度匀速运动，当点F与B重合时停止．在这个运动过程中，正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是（ ）
A．B．C．D．
5．一元二次方程3x2﹣x﹣2＝0的二次项系数是3，它的一次项系数是（ ）
A．﹣1B．﹣2C．1D．0
6．下列四种图案中，不是中心对称图形的为（ ）
A．B．C．D．
7．如图，点A，B，C，D在⊙O上，AB=AC，∠A=40°，CD∥AB，若⊙O的半径为2，则图中阴影部分的面积是( )
A．B．C．D．
8．斜坡坡角等于，一个人沿着斜坡由到向上走了米，下列结论
①斜坡的坡度是； ②这个人水平位移大约米；
③这个人竖直升高米； ④由看的俯角为．
其中正确的个数是（ ）
A．1个B．2个C．3个D．4个
9．如图，一边靠墙(墙有足够长)，其它三边用12 m长的篱笆围成一个矩形(ABCD)花园，这个花园的最大面积是( )
A．16 m2B．12 m2C．18 m2D．以上都不对
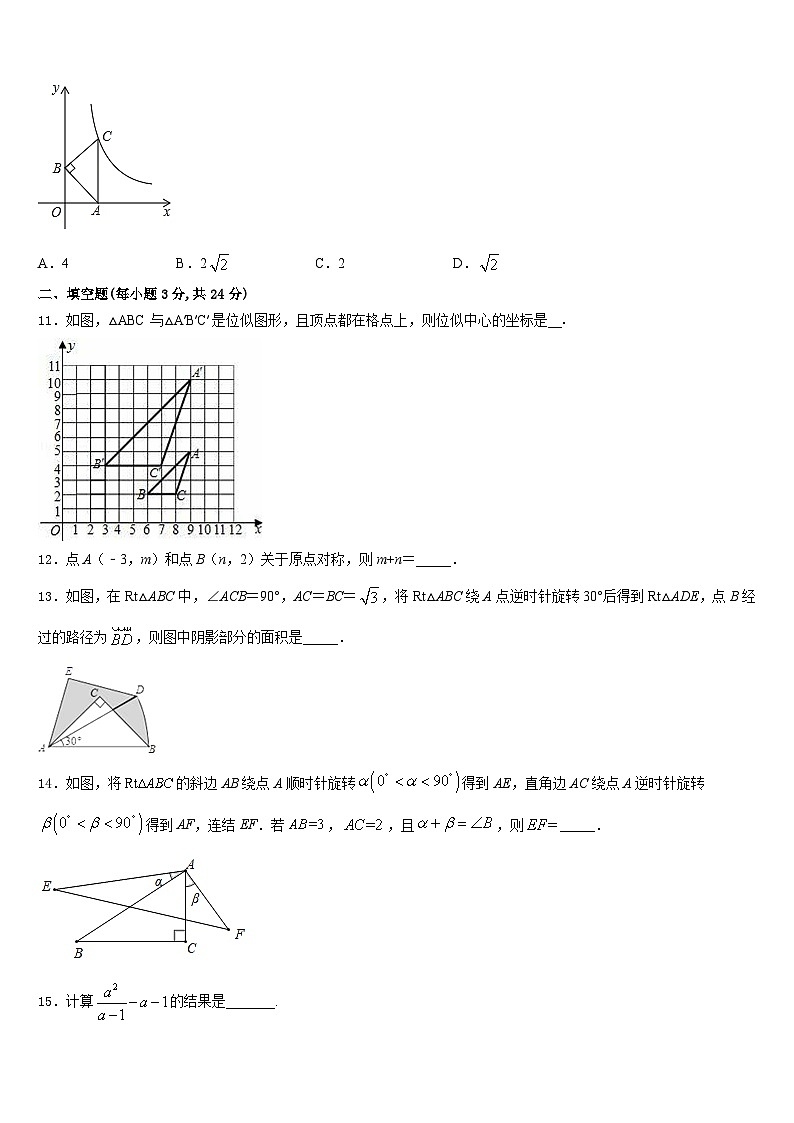
10．如图所示，在平面直角坐标系中，等腰直角三角形ABC的顶点A、B分别在x轴、y轴的正半轴上，∠ABC＝90°，CA⊥x轴于点A，点C在函数y＝（x＞0）的图象上，若OA＝1，则k的值为（ ）
A．4B．2C．2D．
二、填空题(每小题3分,共24分)
11．如图，△ABC与△A′B′C′是位似图形，且顶点都在格点上，则位似中心的坐标是__．
12．点A（﹣3，m）和点B（n，2）关于原点对称，则m+n＝_____．
13．如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝，将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，点B经过的路径为，则图中阴影部分的面积是_____．
14．如图，将的斜边AB绕点A顺时针旋转得到AE，直角边AC绕点A逆时针旋转得到AF，连结EF．若，，且，则_____．
15．计算的结果是_______.
16．如果函数是关于的二次函数，则__________．
17．函数的自变量的取值范围是．
18．一种微粒的半径是1．11114米，这个数据用科学记数法表示为____．
三、解答题(共66分)
19．（10分）已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A(0，3)、B(3，4)、C(2，2)（正方形网格中每个小正方形的边长是一个单位长度）．
（1）画出△ABC向下平移4个单位长度得到的△A1B1C1；
（2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1；
（3）△A2B2C2的面积是 平方单位．
20．（6分）如图，点A是我市某小学，在位于学校南偏西15°方向距离120米的C点处有一消防车.某一时刻消防车突然接到报警电话，告知在位于C点北偏东75°方向的F点处突发火灾，消防队必须立即沿路线CF赶往救火．已知消防车的警报声传播半径为110米，问消防车的警报声对学校是否会造成影响？若会造成影响，已知消防车行驶的速度为每小时60千米，则对学校的影响时间为几秒？（≈3.6，结果精确到1秒）
21．（6分）如图所示是某路灯灯架示意图，其中点A表示电灯，AB和BC为灯架，l表示地面，已知AB＝2m，BC＝5.7m，∠ABC＝110°，BC⊥l于点C，求电灯A与地面l的距离．（结果精确到0.1m．参考数据：sin20°≈0.34，cs20°≈0.94，tan20°≈0.36）
22．（8分）如图，在中，，，，点从点开始沿边向点以的速度移动，同时，点从点开始沿边向点以的速度移动(到达点，移动停止).
(1)如果，分别从，同时出发，那么几秒后，的长度等于？
(2)在(1)中，的面积能否等于？请说明理由.
23．（8分）如图，P是平面直角坐标系中第四象限内一点，过点P作PA⊥x轴于点A，以AP为斜边在右侧作等腰Rt△APQ，已知直角顶点Q的纵坐标为﹣2，连结OQ交AP于B，BQ＝2OB．
（1）求点P的坐标；
（2）连结OP，求△OPQ的面积与△OAQ的面积之比．
24．（8分）如图,点是反比例函数图象上的一点，过点作轴于点，连接，的面积为1．点的坐标为．若一次函数的图象经过点，交双曲线的另一支于点，交轴点．
(1)求反比例函数和一次函数的解析式；
(1)若为轴上的一个动点，且的面积为5，请求出点的坐标．
25．（10分）如图，抛物线经过点，请解答下列问题:
求抛物线的解析式；
抛物线的顶点为点，对称轴与轴交于点，连接，求的长．
点在抛物线的对称轴上运动，是否存在点，使的面积为，如果存在，直接写出点的坐标；如果不存在，请说明理由．
26．（10分）如图，已知抛物线与轴相交于、两点，与轴相交于点，若已知点的坐标为．
（1）求抛物线的解析式；
（2）求线段所在直线的解析式；
（3）在抛物线的对称轴上是否存在点，使为等腰三角形？若存在，求出符合条件的点坐标；若不存在，请说明理由．
参考答案
一、选择题(每小题3分,共30分)
1、C
2、B
3、C
4、C
5、A
6、D
7、B
8、C
9、C
10、C
二、填空题(每小题3分,共24分)
11、（9，0）
12、1
13、
14、
15、
16、1
17、x≠1
18、
三、解答题(共66分)
19、（1）见解析；（2）见解析；（3）1
20、4秒
21、电灯A距离地面l的高度为6.4米．
22、 (1)3秒后，的长度等于；(2)的面积不能等于.
23、（1）点P的坐标（1，﹣4）；（2）△OPQ的面积与△OAQ的面积之比为1．
24、 (1) ，；(1)P(0，5)或(0，1) ．
25、（1）y=-x2+2x+3；（2）2；（3）存在点F，点F（1，2）或（1，-2）
26、（1）；（2）；（3）存在，(2，2)或(2，-2)或(2，0)或(2，)