山东省青岛市即墨区2023-2024学年九年级上学期期末数学试卷

这是一份山东省青岛市即墨区2023-2024学年九年级上学期期末数学试卷，共8页。试卷主要包含了选择题，填空题，作图题，解答题等内容，欢迎下载使用。
1．如图是四个完全相同的小正方体搭成的几何体，它的俯视图为（ ）
A．B．C．D．
2．关于x的一元二次方程x2﹣4x+k＝0无实数解，则k的取值范围是（ ）
A．k＞4B．k＜4C．k＜﹣4D．k＞1
3．已知反比例函数，当x＞0时，y随x的增大而增大,则k的取值范围是（ ）
A．k＞﹣1B．k≥﹣1C．k＜﹣1D．k≤﹣1
4．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DH⊥AB于点H，OH＝4，若菱形ABCD的面积为32，则CD的长为（ ）
A．4B．4C．8D．8
5．张老师有两双完全一样的皮鞋，混在一起后，随手拿两只正好配成一双穿在脚上的概率为（ ）
A．B．C．D．都不对
6．若A（﹣2，y1），B（﹣1，y2），C（2，y3）为二次函数＝x2+2x+2的图象上的三点，则y1，y2，y3的大小关系是（ ）
A．y1＜y2＜y3B．y1＜y3＜y2C．y2＜y1＜y3D．y3＜y1＜y2
7．如图，在Rt△ABC中，∠ACB＝90°，D为AB的中点，过D点作AB的垂线交AC于点E，AC＝16， ，则DE的长为 （ ）
A．B．10C．D．15
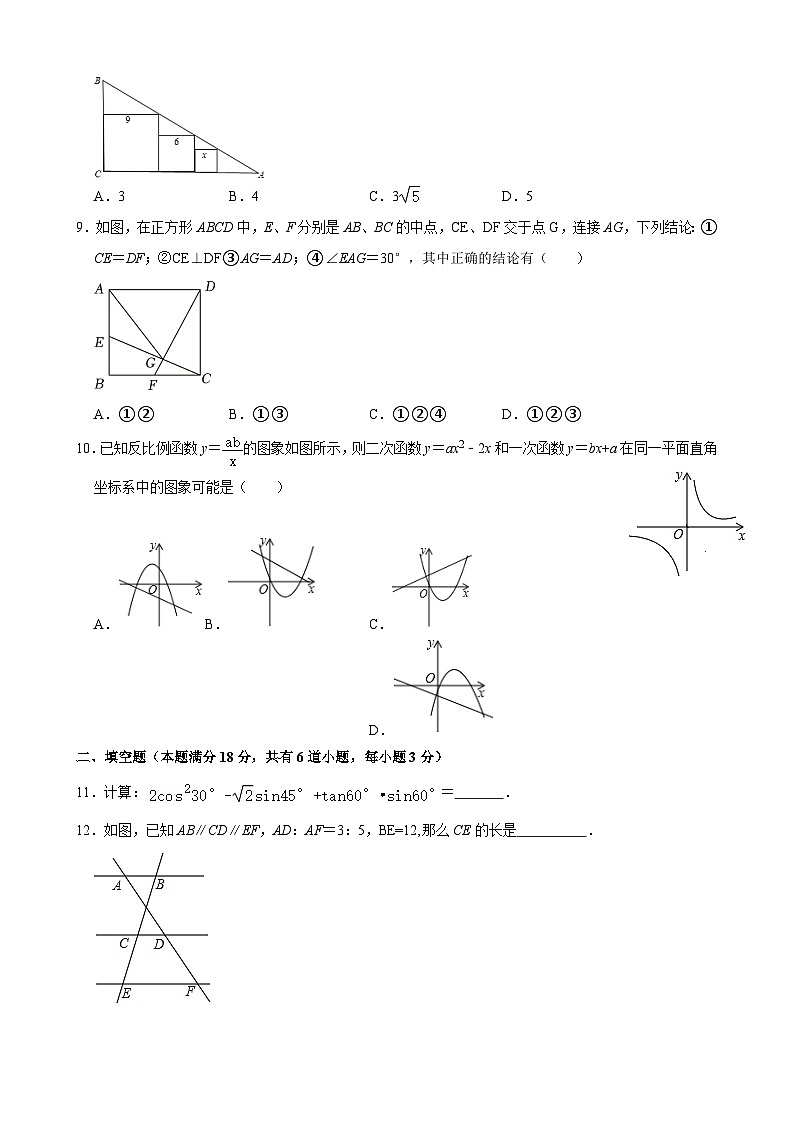
8．如图，在Rt△ABC内画有边长为9，6，x的三个正方形，则x的值为（ ）
A．3B．4C．3D．5
9．如图，在正方形ABCD中，E、F分别是AB、BC的中点，CE、DF交于点G，连接AG，下列结论：①CE＝DF；②CE⊥DF③AG＝AD；④∠EAG＝30°，其中正确的结论有（ ）
A．①②B．①③C．①②④D．①②③
10．已知反比例函数y＝的图象如图所示，则二次函数y＝ax2﹣2x和一次函数y＝bx+a在同一平面直角坐标系中的图象可能是（ ）
A．B．C．D．
二、填空题（本题满分18分，共有6道小题，每小题3分）
11．计算：＝ ．
12．如图，已知AB∥CD∥EF，AD：AF＝3：5，BE=12,那么CE的长是 ．
13．如图，已知第一象限内的点A在反比例函数y＝上，第二象限的点B在反比例函数y＝上，且OA⊥OB，，则k的值为 ．
14．为提高公司经济效益，某公司决定对一种电子产品进行降价促销，根据市场调查：这种电子产品销售单价定为200元时，每天可售出300个；若销售单价每降低1元，每天可多售出5个．已知每个电子产品的固定成本为100元，当这种电子产品降价后的销售单价为多少时，公司每天可获利32000元？若设降价后的销售单价为x元，则可列方程为 ．
15．如图，在△ABC中，∠BAC＝90°，AB=AC点D为边AC的中点，DE⊥BC于点E，则tan∠DBC的值为 ．
16．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x＝1，下列结论：
①abc＜0；
②方程ax2+bx+c＝0（a≠0）必有一个根大于2且小于3；
③若（0，y1），是抛物线上的两点，那么y1＜y2；
④11a+2c＞0；
⑤对于任意实数m，都有m（am+b）≥a+b，
其中正确结论的序号是 ．
三、作图题（4分，用圆规和直尺作图，不写作法，保留痕迹）
17．已知线段a，b，求作矩形ABCD，使对角线AC＝a
四、解答题（本题满分68分）
18．（1）解方程：2x2﹣4x＝1；
（2）在平面直角坐标系中，将抛物线y＝x2﹣4x+1的图象向上平移n（n是正整数）个单位，使平移后的图象与x轴有且只有一个交点
19．从甲、乙、丙、丁4名学生中选2名学生参加一次乒乓球单打比赛，求下列事件发生的概率．
（1）甲一定参加比赛，再从其余3名学生中任意选取1名，恰好选中丙的概率是 ；
（2）任意选取2名学生参加比赛，求一定有乙的概率．（用树状图或列表的方法求解）．
20．在一次数学课外实践活动中，某小组要测量一幢大楼MN的高度，如图，在山坡的坡脚A处测得大楼顶部M处的仰角是58°，沿着山坡向上走75米到达B处，在B处测得大楼顶部M的仰角是22°，已知斜坡AB的坡度i=3:4，求大楼MN的高度．（图中的点A，B，M，N，C均在同一平面内，N，A，C在同一水平线上，参考数据：tan22°≈0.4，tan58°≈1.6）
21．如图，一次函数y1＝kx+1与反比例函数相交于A、B两点，与x轴、y轴交于D、C两点，已知，△BOD的面积为1．
（1）求一次函数和反比例函数的表达式．
（2）请直接写出使y1＞y2的x的取值范围．
22．如图1，点P在正方形ABCD的对角线AC上，正方形ABCD的边长是a，Rt△PEF的两条直角边PE、PF分别交边BC，DC于点M
（1）操作发现：
如图2，固定点P，使△PEF绕点P旋转．
当PM⊥BC，AP＝2PC时，四边形PMCN的边PM长是 ．
②当PM⊥BC，AP＝nPC（n是正实数）时，△PMC的面积是 ．
（2）猜想论证：如图3，将四边形ABCD的形状改变为矩形，AB＝a，AD=b,点P在矩形ABCD的对角线AC上，Rt△PEF的两条直角边PE，PF分别交边BC、DC于点M、N，固定点P，使△PEF绕点P旋转，则＝ ．
23．在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点,过点A作AF∥BC交CE的延长线于点F．
（1）求证：四边形ADBF是菱形；
（2）若AB＝8，菱形ADBF的面积为40．求AC的长．
24．如图，为了绿化小区，某物业公司要在形如五边形ABCDE的草坪上建一个矩形花坛PKDH．已知PH∥AE，PK∥BC，DE＝100m，EA＝60m，BC=70m,CD＝80m．以BC所在直线为x轴，AE所在直线为y轴，坐标原点为O．
（1）求直线AB的表达式；
（2）若设点P的横坐标为x，矩形PKDH的面积为S．
①用x表示S；
②当x为何值时，S取得最大值？
25．小林同学是一名羽毛球运动爱好者，下面是他对击球线路的分析．如图，在平面直角坐标系中，点A、C在x轴上，球网AB与y轴的水平距离OA＝3m，CA=2m,AB＝1.55米，击球点P在y轴上．若选择扣球,羽毛球的飞行高度y1（m）与水平距离x（m）近似满足一次函数关系y1＝﹣0.4x+2.8；若选择吊球，羽毛球的飞行高度y2（m）与水平距离x（m）近似满足二次函数关系，此时当羽毛球飞行的水平距离是1米时,达到最大高度3.2米。
（1）求吊球时羽毛球满足的二次函数的表达式．
（2）请通过计算说明两种击球方式是否过网．
（3）要使球的落地点到C点的距离更近，请通过计算判断应该选择哪种击球方式．
26．如图①，四边形ABCD中，AD∥BC，DC⊥BC，AD＝6cm，DC＝8cm，BC=12cm,动点M在CB上运动，从C点出发到B点，速度为每秒2cm，动点N在BA上运动，从B点出发到A点，速度为每秒1cm．两个动点同时出发，当其中一个点到达终点时，另一个点也随即停止，设两个点的运动时间为t（秒）．
（1）当t为何值时，△BMN是直角三角形？
（2）设△DMN的面积为S，求S与t之间的函数关系式．
（3）如图②，连接BD，是否存在某一时刻t，使MN与BD互相垂直？若存在，求出这时的t值；若不存在说明理由。
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/1/24 19:30:53；用户：15181936486；邮箱：15181936486；学号：21840619