江苏省南京市玄武区2023-2024学年上学期八年级数学+期末+试卷

这是一份江苏省南京市玄武区2023-2024学年上学期八年级数学+期末+试卷，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（2分）36的平方根是（ ）
A．±6B．6C．﹣6D．±
2．（2分）若，且m为整数，则m的值是（ ）
A．1B．2C．3D．4
3．（2分）一次函数y＝﹣2x+3的图象不经过（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
4．（2分）如图，用直尺和圆规作∠AOB的平分线OC，则△DOC≌△EOC的依据是（ ）
A．SSSB．SASC．ASAD．AAS
5．（2分）如图，在△ABC中，∠C＝90°，若BD＝3，DC＝22﹣AD2的值为（ ）
A．13B．21C．25D．29
6．（2分）如图，现有一个计时沙漏，开始时盛满沙子，经过5分钟漏完，则该沙漏中沙面下降的高度h（cm）（min）之间的函数图象大致是（ ）
A．B．
C．D．
7．（2分）如图，在长方形ABCD中，AB＝5，将长方形沿BE折叠，使得点A落在CD边上F处（ ）
A．B．C．D．2
8．（2分）如图，在平面直角坐标系中，点M的坐标为（3，4）（6，0），将△OMN绕点O按逆时针方向旋转得到△OM′N′．若点M′恰好落在x轴上，则点N′的坐标为（ ）
A．（﹣3，5）B．
C．（﹣4，5）D．
二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）
9．（2分）7的算术平方根是 ；27的立方根是 ．
10．（2分）月球的半径约为1738000m，将数据1738000用科学记数法表示为 ．
11．（2分）等腰三角形的两边长分别为4和9，该三角形的周长为 ．
12．（2分）比较大小： 0.5．
13．（2分）在平面直角坐标系中，点P在第四象限，且到x轴的距离为5，则点P的坐标为 ．
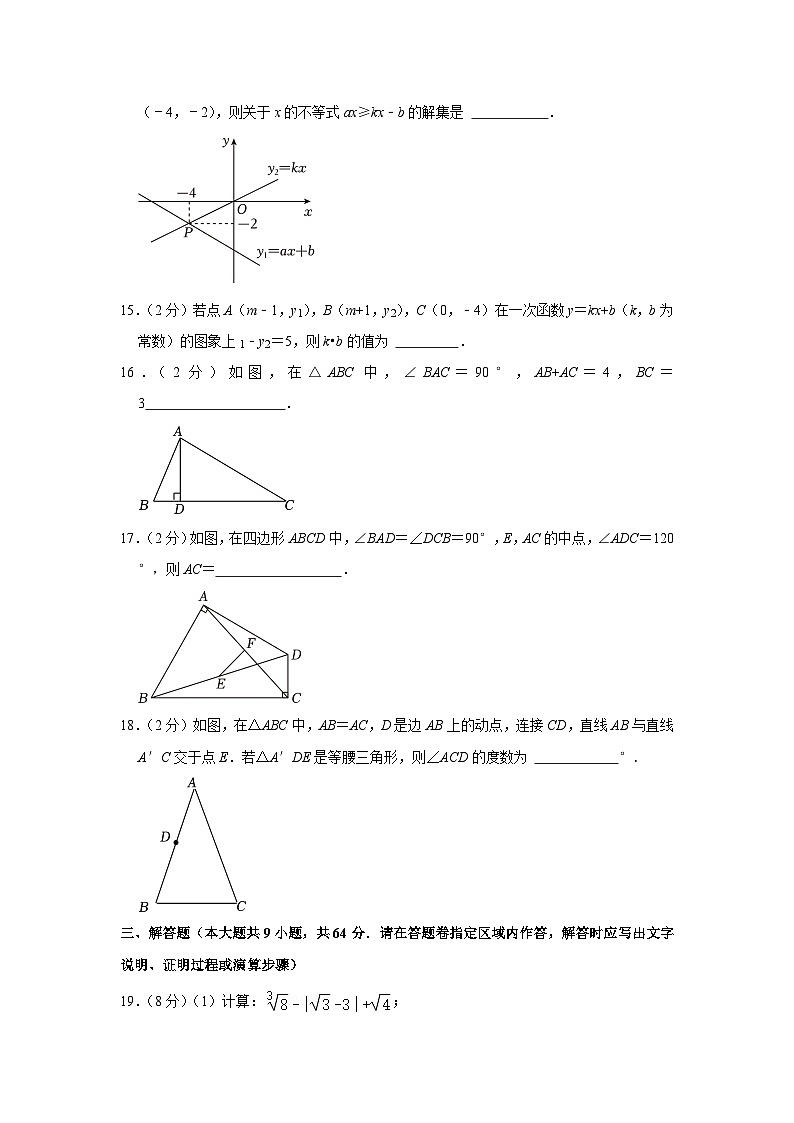
14．（2分）如图，一次函数y1＝ax+b（a，b为常数）与y2＝kx（k为常数）的图象交于点P（﹣4，﹣2），则关于x的不等式ax≥kx﹣b的解集是 ．
15．（2分）若点A（m﹣1，y1），B（m+1，y2），C（0，﹣4）在一次函数y＝kx+b（k，b为常数）的图象上1﹣y2＝5，则k•b的值为 ．
16．（2分）如图，在△ABC中，∠BAC＝90°，AB+AC＝4，BC＝3 ．
17．（2分）如图，在四边形ABCD中，∠BAD＝∠DCB＝90°，E，AC的中点，∠ADC＝120°，则AC＝ ．
18．（2分）如图，在△ABC中，AB＝AC，D是边AB上的动点，连接CD，直线AB与直线A′C交于点E．若△A′DE是等腰三角形，则∠ACD的度数为 °．
三、解答题（本大题共9小题，共64分．请在答题卷指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．（8分）（1）计算：；
（2）求x的值：25（x+1）2＝4．
20．（6分）如图，点D在AB上，点E在AC上，∠B＝∠C．求证BD＝CE．
21．（6分）在边长为1的8×8正方形网格中，点A，B，C均在格点上，将△ABC向左平移4个单位，再向下平移3个单位1B1C1．
（1）画出△A1B1C1，写出点A1的坐标 ；
（2）△A1B1C1的面积为 ；
（3）在y轴上求作点Q，使QB1+QC1的值最小．
22．（6分）在平面直角坐标系中，一次函数的图象经过点（2，﹣1），（0，3）．
（1）求一次函数的表达式；
（2）将一次函数的图象向左平移 个单位长度恰好经过坐标原点．
23．（6分）如图，当秋千OA静止时，最低点A离地面的距离AB为0.7m，点A′与点B的距离A′B为2.5m，点A′水平移动的距离A′C为2m．求秋千OA的长．
24．（6分）如图，已知∠α，线段a．用直尺和圆规按下列要求作图．（保留作图痕迹，写出必要的文字说明）
（1）作出一个等腰三角形ABC，使其底角＝∠α，底边长＝a；
（2）作出一个等腰三角形DEF，使其底角＝∠α，底边上的高＝a．
25．（7分）如图，在△ABC中，AB＝AC，使BC＝CD，连接AD，与AD交于点E．
（1）求证：∠CAD＝∠ABE；
（2）探索线段AE，BE之间的数量关系，并说明理由．
26．（9分）一辆货车和一辆轿车分别从甲、乙两地同时出发，沿同一条直路相向而行，匀速驶向各自目的地乙地和甲地．行驶了一段时间，货车遇到轿车后立即停下帮助维修，故障排除后（km）和货车行驶时间x（h）之间的函数图象如图①所示．
（1）货车的速度为 km/h，轿车的速度为 km/h；
（2）求线段DE的函数表达式；
（3）在图②中，画出货车离乙地的距离s（km）和行驶时间x（h）
27．（10分）【数学概念】
过三角形边上的一点作两条直线，分别与三角形另外两边相交，若截得的两个三角形全等
【理解运用】
在△ABC中，D是边BC上的点，过点D的两条直线DE，AC分别交于点E，F．
（1）如图①，若D是BC的中点，且DE∥AC，求证：D是△ABC的全等点．
（2）如图②，已知△ABC．用直尺和圆规在边BC上作出点D，使D是△ABC的全等点，DF与AB不平行．（保留作图痕迹，写出必要的文字说明）
（3）如图③，D是△ABC的全等点，且AB＜AC，DF与AB不平行，BF与CE交于点P，∠PBC之间的数量关系，并说明理由．
参考答案与试题解析
一、选择题（本大题共8小题，每小题2分，共16分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）
1．（2分）36的平方根是（ ）
A．±6B．6C．﹣6D．±
【分析】根据平方根的定义，求数a的平方根，也就是求一个数x，使得x2＝a，则x就是a的平方根．
【解答】解：∵（±6）2＝36，
∴36的平方根是±7．
故选：A．
【点评】此题考查了平方根的定义．此题注意一个正数的平方根有两个，且它们互为相反数．
2．（2分）若，且m为整数，则m的值是（ ）
A．1B．2C．3D．4
【分析】估算无理数的大小即可得出答案．
【解答】解：∵9＜11＜16，
∴，
∴m＝3．
故选：C．
【点评】本题考查了无理数的估算，无理数的估算常用夹逼法，用有理数夹逼无理数是解题的关键．
3．（2分）一次函数y＝﹣2x+3的图象不经过（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【分析】根据题目中的函数解析式和一次函数的性质，可以得到该函数图象经过哪几个象限，不经过哪个象限．
【解答】解：∵一次函数y＝﹣2x+3，k＝﹣2＜0，
∴该函数图象经过第一、二、四象限，
故选：C．
【点评】本题考查一次函数的性质，解答本题的关键是明确题意一次函数的性质，知道当k＜0，b＞0时，一次函数y＝kx+b的图象经过第一、二、四象限，不经过第三象限．
4．（2分）如图，用直尺和圆规作∠AOB的平分线OC，则△DOC≌△EOC的依据是（ ）
A．SSSB．SASC．ASAD．AAS
【分析】由作图痕迹可知，OD＝OE，CD＝CE，再结合全等三角形的判定可得答案．
【解答】解：由作图痕迹可知，OD＝OE，
∵OC＝OC，
∴△DOC≌△EOC（SSS）．
∴△DOC≌△EOC的依据是SSS．
故选：A．
【点评】本题考查作图—复杂作图、全等三角形的判定，熟练掌握全等三角形的判定、角平分线的作图方法是解答本题的关键．
5．（2分）如图，在△ABC中，∠C＝90°，若BD＝3，DC＝22﹣AD2的值为（ ）
A．13B．21C．25D．29
【分析】在Rt△ABC与Rt△ADC中，由勾股定理得得出AB2与AD2再相减即可推出结论．
【解答】解：在Rt△ABC与Rt△ADC中，由勾股定理得，
AB2＝AC2+BC4，AD2＝AC2+CD4，
∴AB2﹣AD2＝AC8+BC2﹣AC2﹣CD8
＝BC2﹣CD2，
∵BD＝6，CD＝2，
∴BC＝5，
∴BC8﹣CD2＝52﹣22＝21，
故选：B．
【点评】本题考查了勾股定理，利用勾股定理正确得出AB2与AD2是解题的关键．
6．（2分）如图，现有一个计时沙漏，开始时盛满沙子，经过5分钟漏完，则该沙漏中沙面下降的高度h（cm）（min）之间的函数图象大致是（ ）
A．B．
C．D．
【分析】根据一个5分钟沙漏计时器，沙漏中的沙下落的速度可以近似看成匀速，则该沙漏中沙面下降的高度逐渐增大，且增大的速度由慢变快，以此即可选择．
【解答】解：沙漏中的沙下落的速度可以近似看成匀速，则相同时间内，
从计时器开始计时到计时5min止，则该沙漏中沙面下降的高度逐渐增大，故选项B的图象符合题意．
故选：B．
【点评】本题主要考查函数的图象，主要考查了根据实际问题作出函数图象的能力，解题关键是根据题意得出两个变量之间的关系．
7．（2分）如图，在长方形ABCD中，AB＝5，将长方形沿BE折叠，使得点A落在CD边上F处（ ）
A．B．C．D．2
【分析】根据翻折的性质得出AB＝BF＝5，AE＝EF，利用勾股定理即可求出CF，进而求出DF，再次运用勾股定理即可求解．
【解答】解：∵将长方形沿BE折叠，使得点A落在CD边上F处，
∴AB＝BF＝5，AE＝EF，
∴CF＝＝4，
∴DF＝1，
∴AE＝EF＝＝，
解得AE＝，
故选：B．
【点评】本题题考查翻折的性质，勾股定理，熟练掌握翻折的性质是解题关键．
8．（2分）如图，在平面直角坐标系中，点M的坐标为（3，4）（6，0），将△OMN绕点O按逆时针方向旋转得到△OM′N′．若点M′恰好落在x轴上，则点N′的坐标为（ ）
A．（﹣3，5）B．
C．（﹣4，5）D．
【分析】过点M作x轴的垂线，求出OM的长，再用面积法即可解决问题．
【解答】解：过点M作x轴的垂线，垂足为A，垂足为B，
∵M（3，4），
∴MA＝3，OA＝3．
由勾股定理得OM＝5．
∴，
由旋转可知，
S△OM′N′＝S△OMN＝12，OM′＝OM＝5，
则，
∴．
在Rt△N′BO中，
BO＝．
∴点B的坐标为（）．
故选：D．
【点评】本题考查坐标与图形变化﹣旋转，巧用面积法及勾股定理是解题的关键．
二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）
9．（2分）7的算术平方根是 ；27的立方根是 3 ．
【分析】根据立方根的定义和算术平方根的定义进行解题即可．
【解答】解：7的算术平方根是，
27的立方根为：＝3．
故答案为：，7．
【点评】本题考查立方根和算术平方根，熟练掌握相关的知识点是解题的关键．
10．（2分）月球的半径约为1738000m，将数据1738000用科学记数法表示为 1.738×106 ．
【分析】用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|＜10，n为整数，且n比原来的整数位数少1，据此判断即可．
【解答】解：1738000＝1.738×106，
故答案为：4.738×106．
【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
11．（2分）等腰三角形的两边长分别为4和9，该三角形的周长为 22 ．
【分析】分类讨论：9为腰长，9为底边长，根据三角形的周长公式，可得答案．
【解答】解：分两种情况：
①当4为底边长，9为腰长时，
∴三角形的周长＝5+9+9＝22；
②当6为底边长，4为腰长时，
∵4+8＜9，
∴不能构成三角形；
∴这个三角形的周长是22．
故答案为：22．
【点评】本题考查了等腰三角形的性质、三角形的三边关系；熟练掌握等腰三角形的性质，通过进行分类讨论得出结果是解决问题的关键．
12．（2分）比较大小： ＞ 0.5．
【分析】首先把0.5变为，然后估算的整数部分，再根据比较实数大小的方法进行比较即可．
【解答】解：∵0.5＝，2＜，
∴＞3，
∴
故填空答案：＞．
【点评】此题主要考查了实数的大小比较．此题应把0.5变形为分数，然后根据无理数的整数部分再来比较即可解决问题．
13．（2分）在平面直角坐标系中，点P在第四象限，且到x轴的距离为5，则点P的坐标为 （12，﹣5） ．
【分析】先用勾股定理求出点P到y轴的距离，再根据第四象限点的坐标特征，写出点P的坐标．
【解答】解：＝12，
∴点P的坐标为（12，﹣5），
故答案为：（12，﹣5）．
【点评】本题考查了坐标与图形性质，关键求出点P到y轴的距离．
14．（2分）如图，一次函数y1＝ax+b（a，b为常数）与y2＝kx（k为常数）的图象交于点P（﹣4，﹣2），则关于x的不等式ax≥kx﹣b的解集是 x≤﹣4 ．
【分析】直接根据两函数图象的交点即可得出结论．
【解答】解：由函数图象可知，当x＜﹣4时1＝ax+b的图象不在直线y8＝kx的下方，
所以关于x的不等式ax≥kx﹣b的解集是x≤﹣4．
故答案为：x≤﹣4．
【点评】本题考查的是一次函数与一元一不等式，能利用函数图象直接得出不等式的取值范围是解答此题的关键．
15．（2分）若点A（m﹣1，y1），B（m+1，y2），C（0，﹣4）在一次函数y＝kx+b（k，b为常数）的图象上1﹣y2＝5，则k•b的值为 10 ．
【分析】利用一次函数图象上点的坐标特征，可得出y1＝k（m﹣1）+b，y2＝k（m+1）+b，结合y1﹣y2＝5，可求出k值，由点C（0，﹣4）在一次函数y＝kx+b（k，b为常数）的图象上，利用一次函数图象上点的坐标特征，可求出b值，再将k，b的值代入k•b中，即可求出结论．
【解答】解：∵点A（m﹣1，y1），B（m+2，y2）在一次函数y＝kx+b（k，b为常数）的图象上，
∴y1＝k（m﹣2）+b，y2＝k（m+1）+b，
∴y6﹣y2＝k（m﹣1）+b﹣[k（m+6）+b]＝﹣2k＝5，
∴k＝﹣．
又∵点C（0，﹣7）在一次函数y＝kx+b（k，
∴b＝﹣4，
∴k•b＝﹣×（﹣4）＝10．
故答案为：10．
【点评】本题考查了一次函数图象上点的坐标特征，利用一次函数图象上点的坐标特征，求出k，b的值是解题的关键．
16．（2分）如图，在△ABC中，∠BAC＝90°，AB+AC＝4，BC＝3 ．
【分析】根据完全平方公式得出AB•AC的值，再根据等积法求出AD的长即可．
【解答】解：∵AB+AC＝4，
∴（AB+AC）2＝16，
∴AB7+AC2+2AB•AC＝16，
∵AB3+AC2＝BC2＝5，
∴AB•AC＝，
∵S，
∴AD＝＝，
故答案为：．
【点评】本题考查了勾股定理，三角形的面积公式，利用整体思想求解是解题的关键．
17．（2分）如图，在四边形ABCD中，∠BAD＝∠DCB＝90°，E，AC的中点，∠ADC＝120°，则AC＝ 4 ．
【分析】连接AE、CE，由直角三角形斜边上的中线性质得AE＝BD＝BE，CE＝BD＝BE，则∠EAB＝∠EBA，∠EBC＝∠ECB，AE＝CE，再证∠AEC＝120°，则∠EAC＝∠ECA＝30°，然后由等腰三角形的性质得EF⊥AC，AC＝2CF，则CE＝2EF＝4，进而由勾股定理求出CF的长，即可解决问题．
【解答】解：如图，连接AE，
∵∠BAD＝∠DCB＝90°，∠ADC＝120°，
∴∠ABC＝360°﹣90°﹣90°﹣120°＝60°，
∵∠BAD＝∠DCB＝90°，E是BD的中点，
∴AE＝BD＝BEBD＝BE，
∴∠EAB＝∠EBA，∠EBC＝∠ECB，
∴∠EAC＝∠ECA，
∵∠AED＝∠EAB+∠EBA＝2∠EBA，∠CED＝∠EBC+∠ECB＝8∠EBC，
∴∠AEC＝∠AED+∠CED＝2（∠EBA+∠EBC）＝2∠ABC＝120°，
∴∠EAC＝∠ECA＝30°，
∵AE＝CE，F是AC的中点，
∴EF⊥AC，AC＝7CF，
∴∠EFC＝90°，
∴CE＝2EF＝4，
∴CF＝＝＝4，
∴AC＝2CF＝8，
故答案为：4．
【点评】本题考查了勾股定理、等腰三角形的性质、直角三角形斜边上的中线性质、含30°角的直角三角形的性质等知识，熟练掌握等腰三角形的性质和勾股定理是解题的关键，属于中考常考题型．
18．（2分）如图，在△ABC中，AB＝AC，D是边AB上的动点，连接CD，直线AB与直线A′C交于点E．若△A′DE是等腰三角形，则∠ACD的度数为 15或30 °．
【分析】设∠ACD＝α，由折叠的性质可求∠A＝∠A'＝40°，∠ACD＝∠A'CD＝α，∠ADC＝∠A'DC＝140°﹣α，分两种情况讨论，由等腰三角形的性质列出等式，即可求解．
【解答】解：设∠ACD＝α，
∵将△ACD沿CD翻折至△A′CD处，
∴∠A＝∠A'＝40°，∠ACD＝∠A'CD＝α，
∴∠AEA'＝2α+40°，∠A'DE＝100°﹣2α，
当A'E＝A'D，则∠A'ED＝∠AEA'，
∴6α+40°＝100°﹣2α，
∴α＝15°，
当A'E＝DE，则∠A'DE＝∠A'，
∴100°﹣2α＝40°，
∴α＝30°，
故答案为：15°或30°．
【点评】本题考查了翻折变换，等腰三角形的性质，折叠的性质，利用分类讨论思想解决问题是解题的关键．
三、解答题（本大题共9小题，共64分．请在答题卷指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．（8分）（1）计算：；
（2）求x的值：25（x+1）2＝4．
【分析】（1）利用算术平方根及立方根的定义，绝对值的性质计算即可；
（2）利用平方根的定义解方程即可．
【解答】解：（1）原式＝2﹣（3﹣）+2
＝2﹣4++2
＝+1；
（2）原方程变形得：（x+1）8＝，
则x+1＝±，
解得：x＝﹣或x＝﹣．
【点评】本题考查实数的运算及利用平方根的定义解方程，熟练掌握相关运算法则及定义是解题的关键．
20．（6分）如图，点D在AB上，点E在AC上，∠B＝∠C．求证BD＝CE．
【分析】证明△ADC≌△AEB（AAS），可得结论．
【解答】证明：在△ADC和△AEB中，
，
∴△ADC≌△AEB（AAS），
∴AC＝AB，
∵AE＝AD，
∴DB＝CE．
【点评】本题考查全等三角形的判定和性质，解题的关键是掌握全等三角形的判定方法和性质．
21．（6分）在边长为1的8×8正方形网格中，点A，B，C均在格点上，将△ABC向左平移4个单位，再向下平移3个单位1B1C1．
（1）画出△A1B1C1，写出点A1的坐标 （0，0） ；
（2）△A1B1C1的面积为 ；
（3）在y轴上求作点Q，使QB1+QC1的值最小．
【分析】（1）根据平移变换的性质找出对应点即可求解；
（2）根据割补法求解即可；
（3）作点C1关于y轴的对称点C'，连接B1C'交y轴于点Q，则点Q即为所求．
【解答】解：（1）如图所示，△A1B1C2即为所求，A1（0，3），
故答案为：（0，0）；
（2）△A2B1C1的面积为5×2﹣＝，
故答案为：；
（3）如图所示，点Q即为所求．
【点评】本题考查了作图﹣平移变换，轴对称﹣最短路线问题，熟记平移变换的性质是解题的关键．
22．（6分）在平面直角坐标系中，一次函数的图象经过点（2，﹣1），（0，3）．
（1）求一次函数的表达式；
（2）将一次函数的图象向左平移 个单位长度恰好经过坐标原点．
【分析】（1）利用待定系数法求解即可求；
（2）由直线的平移规律得到平移后的解析式y＝﹣2（x+m）+3，代入（0，0），求得m的值，即可求得结论．
【解答】解：（1）设一次函数的表达式为y＝kx+b，
∵经过点（2，﹣1），2）．
∴
解得：．
∴一次函数的表达式为y＝﹣2x+3；
（2）由题意：一次函数的图象向左平移m（m＞0）个单位后的解析式为：y＝﹣4（x+m）+3，
∵经过坐标原点，
∴0＝﹣3（0+m）+3，
∴m＝，
故答案为：．
【点评】本题主要考查了待定系数法求一次函数的解析式，一次函数的图象与几何变换，一次函数图象上点的坐标特征，利用平移规律得到平移后的函数解析式是解题的关键．
23．（6分）如图，当秋千OA静止时，最低点A离地面的距离AB为0.7m，点A′与点B的距离A′B为2.5m，点A′水平移动的距离A′C为2m．求秋千OA的长．
【分析】由勾股定理求出BC＝1.5m，得出AC的长，设OA＝OA'＝x m，则OC＝（x﹣0.8）m，然后在Rt△A'OC中，由勾股定理得出方程，解方程即可．
【解答】解：由题意可知，∠A'CO＝∠A'CB＝90°，
∴BC＝＝＝1.5（m），
∴AC＝BC﹣AB＝1.5﹣6.7＝0.4（m），
设OA＝OA'＝x m，则OC＝（x﹣0.8）m，
在Rt△A'OC中，由勾股定理得：（x﹣8.8）2+32＝x2，
解得：x＝8.9，
答：秋千OA的长为2.4m．
【点评】本题考查了勾股定理的应用，根据勾股定理得出方程是解题的关键．
24．（6分）如图，已知∠α，线段a．用直尺和圆规按下列要求作图．（保留作图痕迹，写出必要的文字说明）
（1）作出一个等腰三角形ABC，使其底角＝∠α，底边长＝a；
（2）作出一个等腰三角形DEF，使其底角＝∠α，底边上的高＝a．
【分析】（1）作∠EBK＝α，在射线BK上截取B，使得BC＝a，在CB的上方作∠FCB＝α，CF交BE一点A，△ABC即为所求；
（2）在图1中，作AH平分∠BAC，如图2中，作MN⊥PQ垂足为O，在射线OP上截取OD，使得OD＝a，在OD 的左侧作∠EDO＝∠BAH，DE交OM一点E，在射线ON上截取OF，使得OF＝OE，连接DF，△DEF即为所求．
【解答】解：（1）如图1中，△ABC即为所求；
（2）如图2中，△DEF即为所求．
【点评】本题考查作图﹣复杂作图，等腰三角形的判定等知识，解题的关键是熟练掌握五种基本作图，属于中考常考题型．
25．（7分）如图，在△ABC中，AB＝AC，使BC＝CD，连接AD，与AD交于点E．
（1）求证：∠CAD＝∠ABE；
（2）探索线段AE，BE之间的数量关系，并说明理由．
【分析】（1）由等腰三角形的性质和外角的性质可求解；
（2）由“SAS”可证△ABE≌△CAH，可得EA＝CH，由直角三角形的性质可证CH＝HE＝HD，即可求解．
【解答】（1）证明：∵AB＝AC，
∴∠ABC＝∠ACB，
∵CE⊥BD，BC＝CD，
∴BE＝DE，
∴∠EBD＝∠EDB，
∵∠ABC＝∠ABE+∠EBD，∠ACB＝∠EDB+∠CAD，
∴∠CAD＝∠ABE；
（2）解：BE＝2AE，理由如下：
如图，在AD上截取AH＝BE，
在△ABE和△CAH中，
，
∴△ABE≌△CAH（SAS），
∴EA＝CH，
∵AH＝BE＝DE，
∴AE＝DH，
∴CH＝DH，
∴∠HCD＝∠HDC，
∵CE⊥BD，
∴∠ECH＝∠CEH，
∴CH＝HE，
∴DE＝2CH，
∴BE＝6AE．
【点评】本题考查了全等三角形的判定和性质，等腰三角形的性质，添加恰当辅助线构造全等三角形是解题的关键．
26．（9分）一辆货车和一辆轿车分别从甲、乙两地同时出发，沿同一条直路相向而行，匀速驶向各自目的地乙地和甲地．行驶了一段时间，货车遇到轿车后立即停下帮助维修，故障排除后（km）和货车行驶时间x（h）之间的函数图象如图①所示．
（1）货车的速度为 60 km/h，轿车的速度为 80 km/h；
（2）求线段DE的函数表达式；
（3）在图②中，画出货车离乙地的距离s（km）和行驶时间x（h）
【分析】（1）根据函数图象先求出货车的速度，再求轿车的速度；
（2）先求出点D，E的坐标，再用待定系数法求函数解析式；
（3）根据货车行驶的时间和路程画出函数图象．
【解答】解：（1）由图象可知，货车的速度为，
轿车的速度为﹣60＝140﹣60＝80（km/h），
故答案为：60，80；
（2）根据题意知，轿车出现故障时行驶了80×2＝160（km），
∴轿车修好后到达甲地所需时间为＝2（h），
∴5﹣2＝6，
∴D（3，0），
货车8小时行驶的路程为2×60＝120（km），
∵160+120＝280（km），
∴E（5，280），
设线段DE的函数表达式为y＝kx+b，
把D，E坐标代入解析式得：，
解得，
∴线段DE的函数表达式为y＝140x﹣420；
（3）由题意得，货车到达乙地的时间为（6+（h），
货车离乙地的距离s（km）和行驶时间x（h）之间的函数图象如图②：
【点评】本题考查一次函数的应用，关键是根据图象读取信息，求出关键点的坐标．
27．（10分）【数学概念】
过三角形边上的一点作两条直线，分别与三角形另外两边相交，若截得的两个三角形全等
【理解运用】
在△ABC中，D是边BC上的点，过点D的两条直线DE，AC分别交于点E，F．
（1）如图①，若D是BC的中点，且DE∥AC，求证：D是△ABC的全等点．
（2）如图②，已知△ABC．用直尺和圆规在边BC上作出点D，使D是△ABC的全等点，DF与AB不平行．（保留作图痕迹，写出必要的文字说明）
（3）如图③，D是△ABC的全等点，且AB＜AC，DF与AB不平行，BF与CE交于点P，∠PBC之间的数量关系，并说明理由．
【分析】（1）由“ASA”可证△BDE≌△DCF，可得结论；
（2）作∠ACB的角平分线交AB于E，作ED∥AC，交BC于D，在AC上截取CF＝BD，连接DF，则点D是△ABC的全等点；
（3）由全等三角形的性质可得BD＝DF，DE＝DC，∠DBE＝∠DFC，可得∠DBF＝∠DFB，由三角形内角和定理可求解．
【解答】（1）证明：∵点D是BC的中点，
∴BD＝CD，
∵DE∥AC，DF∥AB，
∴∠CDE＝∠B，∠EDB＝∠C，
∴△BDE≌△DCF（ASA），
∴D是△ABC的全等点；
（2）解：如图②，作∠ACB的角平分线交AB于E，交BC于D，连接DF；
理由如下：∵CE平分∠ACB，
∴∠ACE＝∠BCE，
∵DE∥AC，
∴∠BDE＝∠DCF，∠DEC＝∠ACE＝∠DCE，
∴DE＝CD，
又∵BD＝CF，
∴△BDE≌△FCD（SAS），
∴点D是△ABC的全等点；
（3）解：∠A＝2∠PBC，理由如下：
∵AB＜AC，DE与AC不平行，
∴∠ABC≠∠ACB，∠ACB≠∠BDE，
∵D是△ABC的全等点，
∴△BDE≌△FDC，
∴BD＝DF，DE＝DC，
∴∠DBF＝∠DFB，∠DEC＝∠DCE，
∴∠DBF＝∠DFB＝∠DEC＝∠DCE，
∵∠DFC+∠AFD＝180°，
∴∠A+∠BDF＝180°，
∵∠PBC+∠DBF+∠BDF＝180°，
∴∠A＝2∠PBC．
【点评】本题是三角形综合题，考查了全等三角形的判定和性质，等腰三角形的性质，理解新定义并运用是解题的关键．