河南省开封市五县2023届高三下学期开学考试数学（文）试卷(含答案)

这是一份河南省开封市五县2023届高三下学期开学考试数学（文）试卷(含答案)，共18页。试卷主要包含了选择题，填空题，双空题，解答题等内容，欢迎下载使用。

一、选择题
1．已知集合,,则( )
A.B.C.D.
2．复数在复平面内对应的点位于( )
A.第一象限B.第二象限C.第三象限D.第四象限
3．已知函数的图象在点处的切线与直线平行,则该切线的方程为( )
A.B.
C.D.
4．我国传统剪纸艺术历史悠久,源远流长,最早可追溯到西汉时期．下图是某一窗花的造型,在长为3,宽为2的矩形中有大小相同的两个圆,两圆均与矩形的其中三边相切,在此矩形内任取一点,则该点取自两圆公共（图中阴影）部分的概率为( )
A.B.C.D.
5．古代名著《九章算术》中记载了求“方亭”体积的问题,方亭是指正四棱台,今有一个方亭型的水库,该水库的下底面的边长为20km,上底面的边长为40km,若水库的最大蓄水量为,则水库深度（棱台的高）为( )
A.10mB.20mC.30mD.40m
6．已知抛物线,过焦点F的直线与C在第四象限交于M点,则( )
A.3B.4C.5D.6
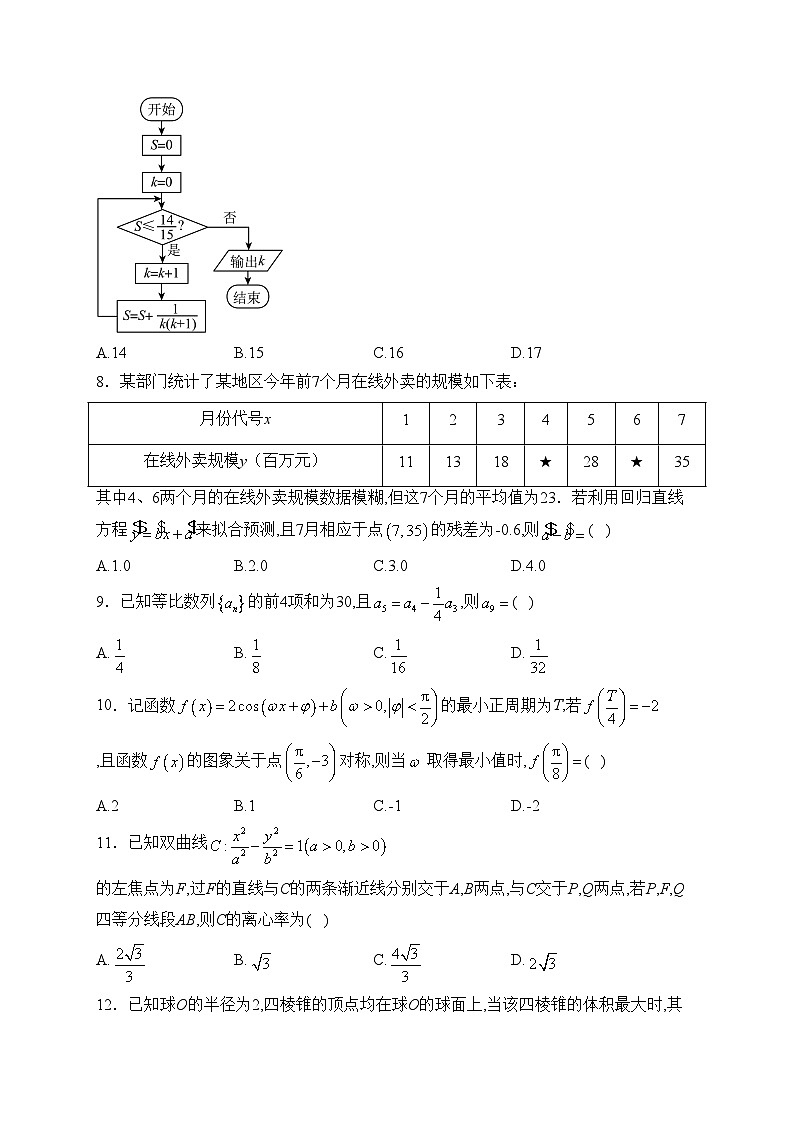
7．执行如图所示的程序框图,则输出的k的值为( )
A.14B.15C.16D.17
8．某部门统计了某地区今年前7个月在线外卖的规模如下表：
其中4、6两个月的在线外卖规模数据模糊,但这7个月的平均值为23．若利用回归直线方程来拟合预测,且7月相应于点的残差为-0.6,则( )
A.1.0B.2.0C.3.0D.4.0
9．已知等比数列的前4项和为30,且,则( )
A.B.C.D.
10．记函数的最小正周期为T,若,且函数的图象关于点对称,则当取得最小值时,( )
A.2B.1C.-1D.-2
11．已知双曲线的左焦点为F,过F的直线与C的两条渐近线分别交于A,B两点,与C交于P,Q两点,若P,F,Q四等分线段AB,则C的离心率为( )
A.B.C.D.
12．已知球O的半径为2,四棱锥的顶点均在球O的球面上,当该四棱锥的体积最大时,其高为( )
A.B.2C.D.
二、填空题
13．已知向量,,若,则实数___________．
14．记为等差数列的前n项和,已知,,则___________．
15．写出与圆和都相切的一条直线的方程___________．
三、双空题
16．已知函数（a,且）是偶函数,则_________,________
四、解答题
17．已知的内角A,B,C的对边分别为a,b,c,．
（1）若,求的值;
（2）证明：为定值．
18．青少年近视问题备受社会各界广泛关注,某研究机构为了解学生对预防近视知识的掌握情况,对某校学生进行问卷调查,并随机抽取200份问卷,发现其得分（满分：100分）都在区间中,并将数据分组,制成如下频率分布表：
（1）估计这200份问卷得分的平均值（同一组中的数据用该组区间的中点值代表）;
（2）用分层抽样的方法从这200份问卷得分在,,内的学生中抽取6人,再从这6人中随机抽取3人进行调查,求这3人来自不同组（3人中没有2人在同一组）的概率.
19．如图,在四棱锥中,底面ABCD,,,,,．
（1）证明：平面平面PBC;
（2）若,求三棱锥的体积．
20．已知函数．
（1）求函数的单调区间;
（2）当时,恒成立,求实数a的取值范围．
21．已知椭圆E的中心为坐标原点O,对称轴分别为x轴、y轴,且过,两点．
（1）求E的方程;
（2）设F为椭圆E的一个焦点,M,N为椭圆E上的两动点,且满足,当M,O,N三点不共线时,求△MON的面积的最大值．
22．在直角坐标系xOy中,曲线C的参数方程为（t为参数）,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线l的极坐标方程为．
（1）求曲线C的普通方程;
（2）若l与C有两个不同公共点,求m的取值范围．
23．已知函数．
（1）求不等式的解集;
（2）设函数,若对任意,都存在,使得成立,求实数a的取值范围．
参考答案
1．答案：B
解析：函数有意义,则,解得,即,
而,
所以.
故选：B.
2．答案：A
解析：依题意,,
所以复数z在复平面内对应的点位于第一象限.
故选：A.
3．答案：C
解析：函数,求导得：,
依题意,,解得,
即有,,
所以函数的图象在点处的切线为：,
即,符合题意.
故选：C.
4．答案：C
解析：如图,矩形面积为,
因为两圆半径相等,结合两圆的位置及圆的对称性可得为等边三角形,
阴影部分面积为,
所以,在此矩形内任取一点,则该点取自两圆公共（图中阴影）部分的概率为
．
故选：C．
5．答案：A
解析：因为正四棱台上下底面边长分别为40km和20km,设高,
因为,,
由棱台的体积计算公式可得：,
解得：,
故选：A.
6．答案：C
解析：因为直线过抛物线的焦点F,则,
所以,,抛物线方程为,因为M在抛物线上且在第四象限,
设点,则,解得：,
由抛物线的定义可知：,
故选：C.
7．答案：B
解析：第1次循环,,;第2次循环,,;
第3次循环,,;第4次循环,,;
第5次循环,,;第6次循环,,;
第7次循环,,;第8次循环,,;
第9次循环,,;第10次循环,,;
第11次循环,,;第12次循环,,;
第13次循环,,;第14次循环,,;
第15次循环,,结束循环,输出,
所以输出的k的值为15.
故选：B.
8．答案：B
解析：依题意,,而,于是得,
而当时,,即,联立解得,
所以.
故选：B.
9．答案：C
解析：设等比数列的公比为q,依题意,,而,解得,
数列的前4项和为,即,解得,
所以.
故选：C.
10．答案：D
解析：由已知得,
因为函数的图象关于对称,所以,
所以,所以,
又因为,所以,,
由的图象关于对称得,
所以,,即有,
又因为,所以当最小时,,此时,
所以,
故选：D．
11．答案：A
解析：双曲线的渐近线,
令半焦距为c,则,
因为直线AB与双曲线C的两个交点P,Q在线段AB上,
则直线AB与双曲线C的左支相交,
因为点P,F,Q四等分线段AB,则由双曲线对称性得,
直线AB垂直于x轴,直线AB的方程为,
不妨令点A在第二象限,由得点,
显然线段FA的中点在双曲线C上,
则有,即,解得,
所以双曲线C的离心率.
故选：A.
12．答案：D
解析：令球O的内接四棱锥为,四边形ABCD外接圆半径为r,,对角线AC,BD的夹角为,
则四边形ABCD的面积,
当且仅当,即四边形ABCD为正方形时取等号,
由球的结构特征知,顶点P为直线与球面O的交点,
并且球心O在线段上,四棱锥的高最大,如图,
,
高,
因此四棱锥的最大体积关系式为：,
令,
则,
求导得,
当时,,当时,,
因此函数在上单调递增,在上单调递减,当时,,此时,
所以当该四棱锥的体积最大时,其高为.
故选：D.
13．答案：
解析：向量,,则,而,
则有,解得,
所以实数.
故答案为：.
14．答案：
解析：设等差数列的公差为d,依题意,,解得,,
所以.
故答案为：.
15．答案：（答案不唯一）
解析：圆的圆心,半径,圆的圆心,半径,
则,因此圆,相外切,它们有3条公切线,而轴,,
则两圆的每条公切线斜率都存在,设公切线方程为,k,t为常数,
于是得,整理得或,
解得,解得：或,
因此圆,的公切线方程为：或或,
所以与圆和都相切一条直线的方程可以为.
故答案为：.
16．答案：①.8②.
解析：因为函数（a,且）是偶函数,
则函数对定义域内任意实数恒有成立,
即,
整理得,
,显然不恒为0,
因此恒成立,
而b为常数,则必有为常数,于是得,又,解得,,
此时,其定义域为且,
,即函数是偶函数,所以,.
故答案为：8;
17．答案：（1）
（2）见解析
解析：（1）由,
,,即,
,所以,
所以,
又,,
,
,
,解得;
（2）由已知条件得,
,
,
,
,
,,
由余弦定理得,
由正弦定理得,
整理得 ,
即为定值．
18．答案：（1）74.5;
（2）.
解析：（1）由频率分布表得：,
所以200份问卷得分的平均值约为：.
（2）由（1）知,问卷得分在,,内的频率分别为0.20,0.30,0.10,
因此抽取的6人中,得分在,,内的人数分别为2人,3人,1人,
记得分在内的2人为,得分在内的3人为,,得分在内的1人为,
从6人中任取3人的不同结果为：,,,,,
,,,,,,,
,,,,,共20个,它们等可能,
抽取的3人来自不同组的事件A有：,,,,,共6个,
所以3人来自不同组的概率.
19．答案：（1）证明见解析
（2）
（1）连接BD,因为,所以,
又因为,,所以,即,
又因为底面ABCD,底面ABCD,所以,
又因为CD,平面PCD,,
所以平面PCD,又因为平面PBC,
所以平面平面PBC.
（2）在直角三角形ABD中,,
在直角三角形BCD中,,
所以
,
所以,
所以.
20．答案：（1）函数在上单调递减,在上单调递增;
（2）
解析：（1）由函数
可得,令,
则,令,得;令,得,
所以函数在上单调递减,在上单调递增,
则,所以在R上恒成立;
当时,则有;当时,则有,
所以函数在上单调递减,在上单调递增;
（2）因为当时,恒成立,
即在上恒成立,
也即在上恒成立,
令,
则,
令,则,
令,得;令,得,
所以在上单调递减,在上单调递增,
则,所以,则在上单调递增,
所以,故.
21．答案：（1）
（2）
解析：（1）设椭圆方程为,
因为椭圆过点,,
所以,
解得：,所以椭圆E的方程为：.
（2）不妨设F为椭圆的下焦点,由(1)可知：点,则,
因为,则,所以,
设直线MN的方程为：,,
联立方程组,整理可得：,
则,即（*）,
由韦达定理可得：,,
由弦长公式可得：,
点O到直线MN的距离,
所以,
所以当时,面积最大,最大为.
22．答案：（1）
（2）
解析：（1）由
可得,即,
因为,则,当且仅当时,等号成立,
故曲线C的普通方程为.
（2）因为直线l的极坐标方程为,
所以,直线l的普通方程为,
联立可得,
设直线l与曲线C交于点、,
由题意可得,解得.
因此,实数m的取值范围为.
23．答案：（1）;
（2）.
解析：（1）依题意,函数,
则不等式化为：或或,
解得或或,则,
所以不等式的解集为.
（2）由（1）知,当时,,当时,,当时,,
因此函数值域为,
,,
当且仅当时取等号,
因此函数的值域为,
因为对任意,都存在,使得成立,则有,
即,解得,
所以实数a的取值范围是.
月份代号x
1
2
3
4
5
6
7
在线外卖规模y（百万元）
11
13
18
★
28
★
35
分数
频率
0.15
0.25
m
0.30
0.10