
2023-2024学年河北省廊坊市永清县九上数学期末考试试题含答案
展开
这是一份2023-2024学年河北省廊坊市永清县九上数学期末考试试题含答案,共8页。
学校_______ 年级_______ 姓名_______
注意事项:
1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每题4分,共48分)
1.在同一平面直角坐标系内,将函数y=2x2+4x﹣3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是( )
A.(﹣3,﹣6)B.(1,﹣4)C.(1,﹣6)D.(﹣3,﹣4)
2.已知x1,x2是一元二次方程的两根,则x1+x2的值是( )
A.0B.2C.-2D.4
3.在△ABC中,tanC=,csA=,则∠B=( )
A.60°B.90°C.105°D.135°
4.半径为R的圆内接正六边形的面积是( )
A.R2B.R2C.R2D.R2
5.函数(k为常数)的图像上有三个点(-2,y1),(-1,y2),(,y3),函数值y1,y2,y3的大小为( )
A.B.
C.D.
6.不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( )
A.摸出的是3个白球B.摸出的是3个黑球
C.摸出的是2个白球、1个黑球D.摸出的是2个黑球、1个白球
7.在Rt△ABC中,∠C=90°,AC=3,BC=4,那么csB的值是( )
A.B.C.D.
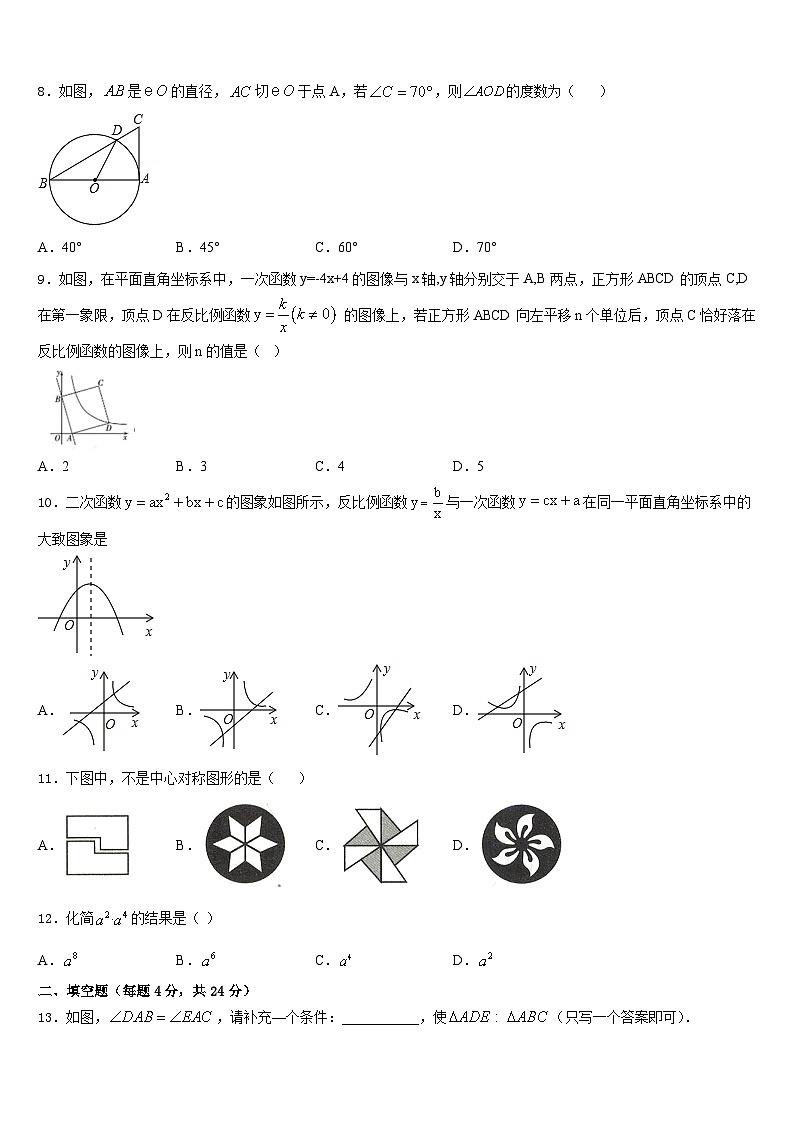
8.如图,是的直径,切于点A,若,则的度数为( )
A.40°B.45°C.60°D.70°
9.如图,在平面直角坐标系中,一次函数y=-4x+4的图像与x轴,y轴分别交于A,B两点,正方形ABCD的顶点C,D在第一象限,顶点D在反比例函数 的图像上,若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数的图像上,则n的值是( )
A.2B.3C.4D.5
10.二次函数的图象如图所示,反比例函数与一次函数在同一平面直角坐标系中的大致图象是
A.B.C.D.
11.下图中,不是中心对称图形的是( )
A.B.C.D.
12.化简的结果是( )
A.B.C.D.
二、填空题(每题4分,共24分)
13.如图,,请补充—个条件:___________,使(只写一个答案即可).
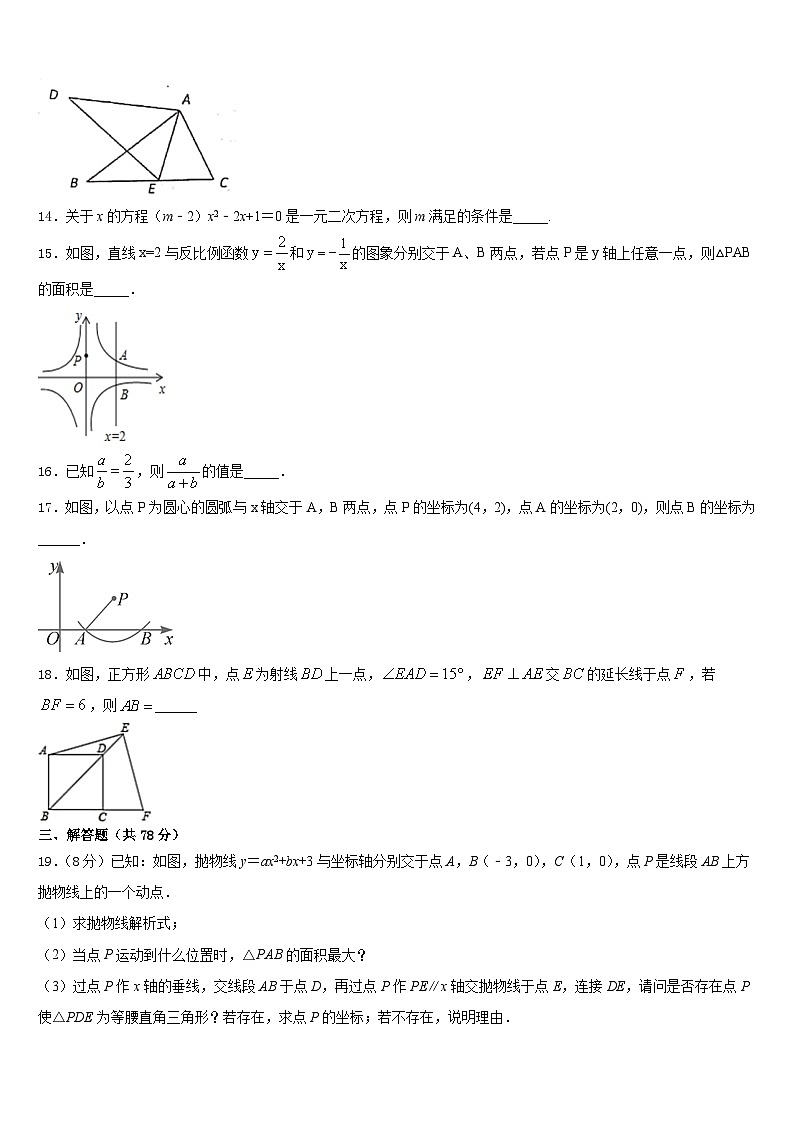
14.关于x的方程(m﹣2)x2﹣2x+1=0是一元二次方程,则m满足的条件是_____.
15.如图,直线x=2与反比例函数和的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是_____.
16.已知,则的值是_____.
17.如图,以点P为圆心的圆弧与x轴交于A,B两点,点P的坐标为(4,2),点A的坐标为(2,0),则点B的坐标为______.
18.如图,正方形中,点为射线上一点,,交的延长线于点,若,则______
三、解答题(共78分)
19.(8分)已知:如图,抛物线y=ax2+bx+3与坐标轴分别交于点A,B(﹣3,0),C(1,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线解析式;
(2)当点P运动到什么位置时,△PAB的面积最大?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连接DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求点P的坐标;若不存在,说明理由.
20.(8分)如图1,抛物线与轴交于,两点,过点的直线分别与轴及抛物线交于点
(1)求直线和抛物线的表达式
(2)动点从点出发,在轴上沿的方向以每秒1个单位长度的速度向左匀速运动,设运动时间为秒,当为何值时,为直角三角形?请直接写出所有满足条件的的值.
(3)如图2,将直线沿轴向下平移4个单位后,与轴,轴分别交于,两点,在抛物线的对称轴上是否存在点,在直线上是否存在点,使的值最小?若存在,求出其最小值及点,的坐标,若不存在,请说明理由.
21.(8分)如图,抛物线y=ax2+bx+c (a≠0)过点M(-2,3),顶点坐标为N(-1,4),且与x轴交于A、B两点,与y轴交于C点.
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上的动点,当PM+PB的值最小时,求点P的坐标;
22.(10分)如图,抛物线l:y=﹣x2+bx+c(b,c为常数),其顶点E在正方形ABCD内或边上,已知点A(1,2),B(1,1),C(2,1).
(1)直接写出点D的坐标_____________;
(2)若l经过点B,C,求l的解析式;
(3)设l与x轴交于点M,N,当l的顶点E与点D重合时,求线段MN的值;当顶点E在正方形ABCD内或边上时,直接写出线段MN的取值范围;
(4)若l经过正方形ABCD的两个顶点,直接写出所有符合条件的c的值.
23.(10分)A箱中装有3张相同的卡片,它们分别写有数字1,2,4;B箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从A箱、B箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
(1)两张卡片上的数字恰好相同的概率.
(2)如果取出A箱中卡片上的数字作为十位上的数字,取出B箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率.
24.(10分)在正方形和等腰直角中,,是的中点,连接、.
(1)如图1,当点在边上时,延长交于点.求证:;
(2)如图2,当点在的延长线上时,(1)中的结论是否成立?请证明你的结论;
(3)如图3,若四边形为菱形,且,为等边三角形,点在的延长线上时,线段、又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.
25.(12分)关于的一元二次方程
(1)若方程的一个根为1,求方程的另一个根和的值
(2)求证:不论取何实数,方程总有两个不相等的实数根.
26.(12分)岚山区地处黄海之滨,渔业资源丰富,海产品深受消费者喜爱.某海产品批发超市对进货价为40元/千克的某品牌小黄鱼的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式;
(2)若不考虑其它因素,则销售总利润=每千克的利润×总销量,那么当销售价格定为多少时,该品牌小黄鱼每天的销售利润最大?最大利润是多少?
参考答案
一、选择题(每题4分,共48分)
1、C
2、B
3、C
4、C
5、B
6、A
7、A
8、A
9、B
10、B
11、D
12、B
二、填空题(每题4分,共24分)
13、∠D=∠B或∠AED=∠C或AD:AB=AE:AC或AD•AC=AB•AE(填一个即可).
14、
15、.
16、
17、 (6,0)
18、
三、解答题(共78分)
19、(1)y=﹣x2﹣2x+3 (2)(﹣,) (3)存在,P(﹣2,3)或P(,)
20、(1),;(2)或3或4或12;(3)存在,,,最小值
21、(1)二次函数的解析式为:;(2)点P的坐标为(-1,2)
22、(1)D点的坐标为(1,1);(1)y=﹣x1+3x﹣1;(3)1≤MN≤;(4)所有符合条件的c的值为﹣1,1,﹣1.
23、(1);(2).
24、(1)证明见解析;(2)成立,证明见解析;(3),图详见解析.
25、(1),另一个根是;(2)详见解析.
26、(1)y=-2x+140;(2)当该种小黄鱼销售价定为55元/千克时,每天的销售利润有最大值1元
相关试卷
这是一份2023-2024学年河北省廊坊市九上数学期末教学质量检测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
这是一份河北省廊坊市永清县2023-2024学年八上数学期末综合测试模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
这是一份河北省廊坊市永清县第五中学2023-2024学年上学期九年级12月月考数学试题,共4页。










