2023-2024学年河南省沁阳市九年级数学第一学期期末联考模拟试题含答案

这是一份2023-2024学年河南省沁阳市九年级数学第一学期期末联考模拟试题含答案，共7页。
学校_______ 年级_______ 姓名_______
请考生注意：
1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。
一、选择题（每题4分，共48分）
1．如图，点，，均在⊙上，当时，的度数是（ ）
A．B．C．D．
2．的半径为，弦，，，则、间的距离是：（ ）
A．B．C．或D．以上都不对
3．如图，已知与位似，位似中心为点且的面积与面积之比为，则的值为（ ）
A．B．
C．D．
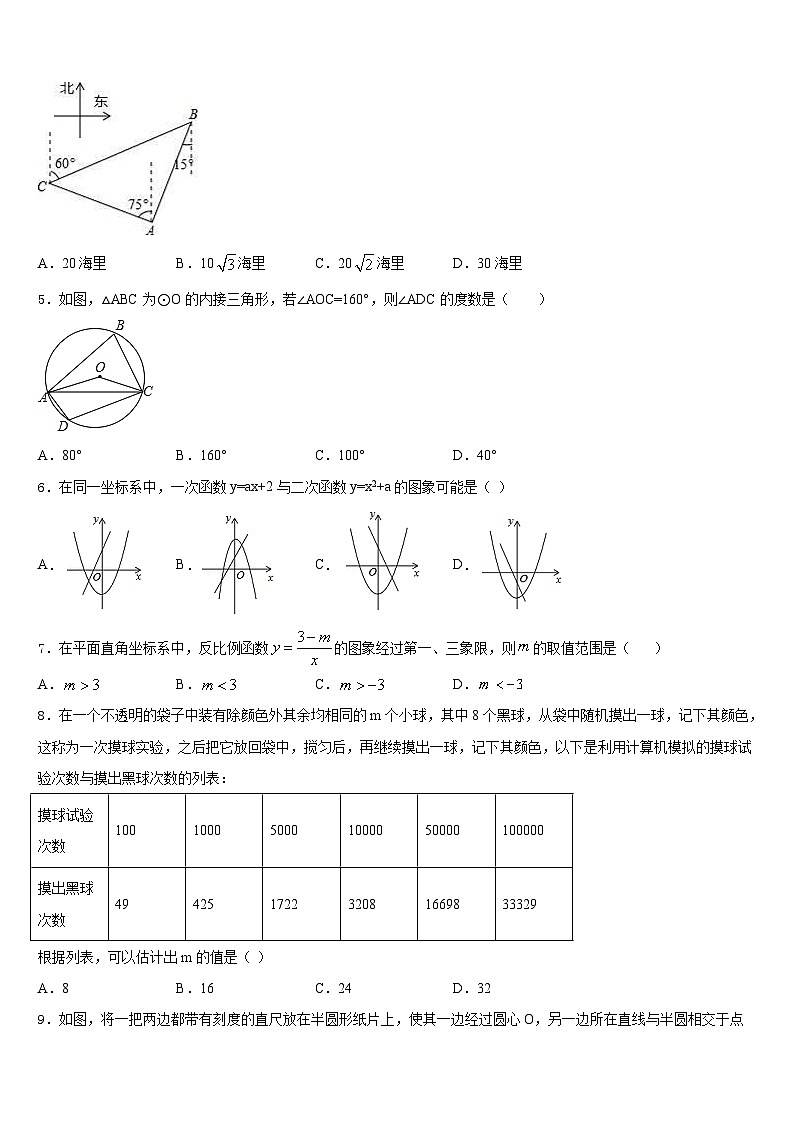
4．如图，在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处，若渔船沿北偏西75°方向以40海里/小时的速度航行，航行半小时后到达C处，在C处观测到B在C的北偏东60°方向上，则B、C之间的距离为（ ）.
A．20海里B．10海里C．20海里D．30海里
5．如图，△ABC为⊙O的内接三角形，若∠AOC=160°，则∠ADC的度数是（ ）
A．80°B．160°C．100°D．40°
6．在同一坐标系中，一次函数y=ax+2与二次函数y=x2+a的图象可能是（ ）
A．B．C．D．
7．在平面直角坐标系中，反比例函数的图象经过第一、三象限，则的取值范围是（ ）
A．B．C．D．
8．在一个不透明的袋子中装有除颜色外其余均相同的m个小球，其中8个黑球，从袋中随机摸出一球，记下其颜色，这称为一次摸球实验，之后把它放回袋中，搅匀后，再继续摸出一球，记下其颜色，以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表：
根据列表，可以估计出m的值是（ ）
A．8B．16C．24D．32
9．如图，将一把两边都带有刻度的直尺放在半圆形纸片上，使其一边经过圆心O，另一边所在直线与半圆相交于点D、E，量出半径OC=5cm，弦DE=8cm，则直尺的宽度是( )

A．4cmB．3cmC．2cmD．1cm
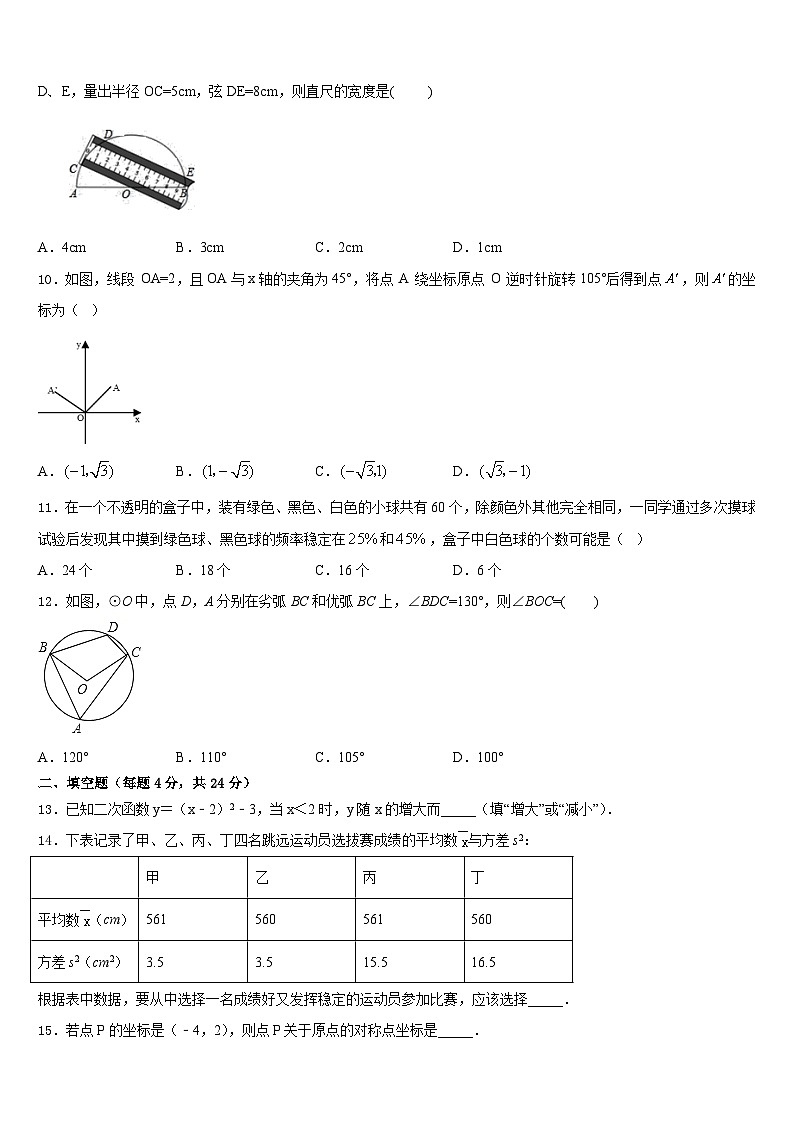
10．如图，线段 OA=2，且OA与x轴的夹角为45°，将点 A 绕坐标原点 O 逆时针旋转105°后得到点，则的坐标为（ ）
A．B．C．D．
11．在一个不透明的盒子中，装有绿色、黑色、白色的小球共有60个，除颜色外其他完全相同，一同学通过多次摸球试验后发现其中摸到绿色球、黑色球的频率稳定在和，盒子中白色球的个数可能是（ ）
A．24个B．18个C．16个D．6个
12．如图，⊙O中，点D，A分别在劣弧BC和优弧BC上，∠BDC=130°，则∠BOC=( )
A．120°B．110°C．105°D．100°
二、填空题（每题4分，共24分）
13．已知二次函数y＝（x﹣2）2﹣3，当x＜2时，y随x的增大而_____（填“增大”或“减小”）．
14．下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s2：
根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择_____．
15．若点P的坐标是（﹣4，2），则点P关于原点的对称点坐标是_____．
16．如图，已知在中，.以为直径作半圆，交于点.若，则的度数是________度．
17．如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是_____________．
18．已知线段a＝4 cm，b＝9 cm，则线段a，b的比例中项为_________cm．
三、解答题（共78分）
19．（8分）如图①，四边形是边长为2的正方形，，四边形是边长为的正方形，点分别在边上，此时，成立．
（1）当正方形绕点逆时针旋转，如图②，成立吗？若成立，请证明；若不成立，请说明理由；
（2）当正方形绕点逆时针旋转（任意角）时，仍成立吗？直接回答；
（3）连接，当正方形绕点逆时针旋转时，是否存在∥，若存在，请求出的值；若不存在，请说明理由．
20．（8分）如图，二次函数的图象交轴于点，交轴于点是直线下方抛物线上一动点．
（1）求这个二次函数的表达式;
（2）连接，是否存在点，使面积最大，若存在，求出点的坐标;若不存在，请说明理由．
21．（8分）一玩具厂去年生产某种玩具，成本为元/件，出厂价为元/件，年销售量为万件．今年计划通过适当增加成本来提高产品档次，以拓展市场．若今年这种玩具每件的成本比去年成本增加倍，今年这种玩具每件的出厂价比去年出厂价相应提高倍，则预计今年年销售量将比去年年销售量增加倍（本题中）．
用含的代数式表示，今年生产的这种玩具每件的成本为________元，今年生产的这种玩具每件的出厂价为________元．
求今年这种玩具的每件利润元与之间的函数关系式．
设今年这种玩具的年销售利润为万元，求当为何值时，今年的年销售利润最大？最大年销售利润是多少万元？
注：年销售利润（每件玩具的出厂价-每件玩具的成本）年销售量．
22．（10分）计算:
23．（10分）已知关于x的一元二次方程x2+(2m+3)x+m2＝1有两根α，β
(1)求m的取值范围；
(2)若α+β+αβ＝1．求m的值．
24．（10分）已知关于x的一元二次方程.
（1）求证：方程总有两个不相等的实数根.
（2）若此方程的一个根是1，求出方程的另一个根及m的值.
25．（12分）已知：为的直径，,为上一动点（不与、重合）.

（1）如图1，若平分，连接交于点.①求证：；②若，求的长；
（2）如图2，若绕点顺时针旋转得，连接.求证：为的切线.
26．（12分）解方程:.
参考答案
一、选择题（每题4分，共48分）
1、A
2、C
3、A
4、C
5、C
6、C
7、B
8、C
9、B
10、C
11、B
12、D
二、填空题（每题4分，共24分）
13、减小
14、甲
15、（4，﹣2） ．
16、1
17、或或1
18、6
三、解答题（共78分）
19、（1）成立，证明见解析；（2）结论仍成立；（3）存在，
20、（1）；（2）存在点，使面积最大，点的坐标为．
21、10＋7x 12＋6x
22、
23、 (1)m≥﹣；(2)m的值为2．
24、（1）证明见解析；（2），2；
25、（1）①见解析，②2；（2）见解析
26、,
摸球试验次数
100
1000
5000
10000
50000
100000
摸出黑球次数
49
425
1722
3208
16698
33329
甲
乙
丙
丁
平均数（cm）
561
560
561
560
方差s2（cm2）
3.5
3.5
15.5
16.5