2023-2024学年浙江省台州市天台县数学九年级第一学期期末联考模拟试题含答案

这是一份2023-2024学年浙江省台州市天台县数学九年级第一学期期末联考模拟试题含答案，共8页。试卷主要包含了考生必须保证答题卡的整洁，抛物线的开口方向是，如图，四边形内接于⊙，等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。
4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题（每题4分，共48分）
1．一元二次方程的根的情况是( )
A．有两个相等的实根B．有两个不等的实根C．只有一个实根D．无实数根
2．某林业部门要考察某幼苗的成活率，于是进行了试验，下表中记录了这种幼苗在一定条件下移植的成活情况，则下列说法不正确的是（ ）
A．由此估计这种幼苗在此条件下成活的概率约为0.9
B．如果在此条件下再移植这种幼苗20000株，则必定成活18000株
C．可以用试验次数累计最多时的频率作为概率的估计值
D．在大量重复试验中，随着试验次数的增加，幼苗成活的频率会越来越稳定，因此可以用频率估计概率
3．将半径为5的圆形纸片，按如图方式折叠，若和都经过圆心，则图中阴影部分的面积是( )
A．B．C．D．
4．若将抛物线的函数图象先向右平移1个单位，再向下平移2个单位后，可得到一个新的抛物线的图象，则所得到的新的抛物线的解析式为( )
A．B．
C．D．
5．用配方法解下列方程时，配方有错误的是（ ）
A．化为B．化为
C．化为D．化为
6．我们研究过的图形中，圆的任何一对平行切线的距离总是相等的，所以圆是“等宽曲线”.除了圆以外，还有一些几何图形也是“等宽曲线”，如勒洛三角形(如图)，它是分别以等边三角形的每个顶点为圆心，以边长为半径，在另两个顶点间画一段圆弧，三段圆弧围成的曲边三角形. 图是等宽的勒洛三角形和圆形滚木的截面图.
图 图
有如下四个结论：
①勒洛三角形是中心对称图形
②图中，点到上任意一点的距离都相等
③图中，勒洛三角形的周长与圆的周长相等
④使用截面是勒洛三角形的滚木来搬运东西，会发生上下抖动
上述结论中，所有正确结论的序号是（ ）
A．①②B．②③C．②④D．③④
7．抛物线的开口方向是（ ）
A．向下B．向上C．向左D．向右
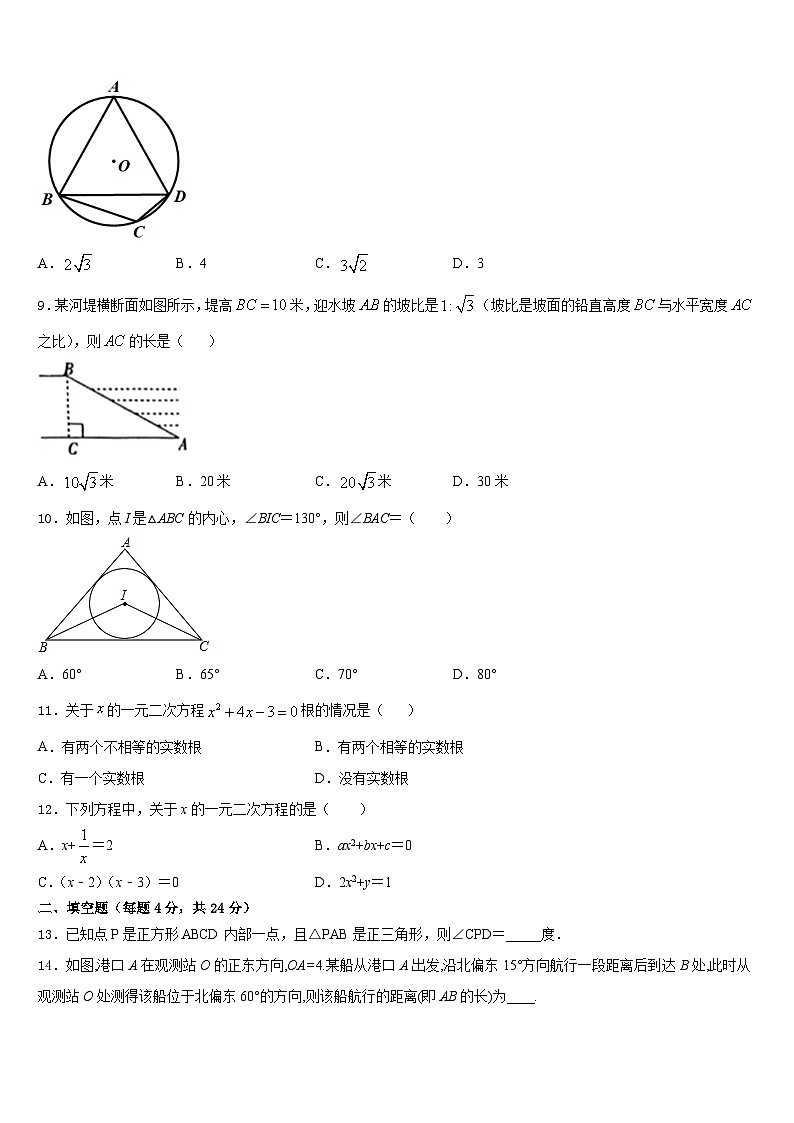
8．如图，四边形内接于⊙，．若⊙的半径为2，则的长为（ ）
A．B．4C．D．3
9．某河堤横断面如图所示，堤高米，迎水坡的坡比是（坡比是坡面的铅直高度与水平宽度之比），则的长是（ ）
A．米B．20米C．米D．30米
10．如图，点I是△ABC的内心，∠BIC＝130°，则∠BAC＝（ ）
A．60°B．65°C．70°D．80°
11．关于的一元二次方程根的情况是（ ）
A．有两个不相等的实数根B．有两个相等的实数根
C．有一个实数根D．没有实数根
12．下列方程中，关于x的一元二次方程的是（ ）
A．x+＝2B．ax2+bx+c＝0
C．（x﹣2）（x﹣3）＝0D．2x2+y＝1
二、填空题（每题4分，共24分）
13．已知点P是正方形ABCD内部一点，且△PAB是正三角形，则∠CPD＝_____度．
14．如图,港口A在观测站O的正东方向,OA=4.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为____.

15．如图，菱形ABCD中，对角线AC，BD相交于点O，点E，F分别是的边AB，BC边的中点若，
，则线段EF的长为______．
16．如图，以矩形ABCD的顶点A为圆心，线段AD长为半径画弧，交AB边于F点；再以顶点C为圆心，线段CD长为半径画弧，交AB边于点E，若AD＝，CD＝2，则DE、DF和EF围成的阴影部分面积是_____．
17．如图，河坝横断面迎水坡AB的坡比是1:（坡比是坡面的铅直高度BC与水平宽度AC之比），坝高BC=3m，则坡面AB的长度是 ．
18．如图，将矩形纸片ABCD(AD>DC)的一角沿着过点D的直线折叠，使点A与BC边上的点E重合，折痕交AB于点F.若BE:EC=m:n，则AF:FB=
三、解答题（共78分）
19．（8分）如图，已知点A（a，3）是一次函数y1＝x+1与反比例函数y2＝的图象的交点．（1）求反比例函数的解析式；（2）在y轴的右侧，当y1＞y2时，直接写出x的取值范围；（3）求点A与两坐标轴围成的矩形OBAC的面积．
20．（8分）为了满足师生的阅读需求，某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.
（1）求这两年藏书的年均增长率；
（2）经统计知：中外古典名著的册数在2016年底仅占当时藏书总量的5.6%，在这两年新增加的图书中，中外古典名著所占的百分率恰好等于这两年藏书的年均增长率，那么到2018年底中外古典名著的册数占藏书总量的百分之几？
21．（8分）如图，在Rt△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm.动点M从点B出发，在线段BA上以每秒3cm的速度点A运动，同时动点N从点C出发，在线段CB上以每秒2cm的速度向点B运动，其中一点到达终点后，另一点也停止运动.运动时间为t秒，连接MN.
（1）填空：BM= cm.BN= cm.（用含t的代数式表示）
（2）若△BMN与△ABC相似，求t的值；
（3）连接AN，CM，若AN⊥CM，求t的值．
22．（10分）如图，抛物线与轴交于点和，与轴交于点顶点为．
求抛物线的解析式；
求的度数；
若点是线段上一个动点，过作轴交抛物线于点，交轴于点，设点的横坐标为．
①求线段的最大值；
②若是等腰三角形，直接写出的值．
23．（10分） “垃圾分类”越来越受到人们的关注，我市某中学对部分学生就“垃圾分类”知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图．根据图中信息回答下列问题：
（1）接受问卷调查的学生共有 人，条形统计图中的值为 ；
（2）扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为 ；
（3）若从对垃圾分类知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加垃圾分类知识竞赛，请用列表或画树状图的方法，求恰好抽到1名男生和1名女生的概率．
24．（10分）如图，反比例函数的图象的一支在平面直角坐标系中的位置如图所示，根据图象回答下列问题：
（1）图象的另一支在第________象限；在每个象限内，随的增大而________，常数的取值范围是________；
（2）若此反比例函数的图象经过点，求的值．
25．（12分）如图，在▱ABCD中 过点A作AE⊥DC，垂足为E，连接BE，F为BE上一点，且∠AFE=∠D．
（1）求证：△ABF∽△BEC；
（2）若AD=5，AB=8，sinD=，求AF的长．
26．（12分）一个不透明的袋子中装有红、白两种颜色的小球，这些球除颜色外都相同，其中红球有1个，若从中随机摸出一个球，这个球是白球的概率为．
（1）求袋子中白球的个数；（请通过列式或列方程解答）
（2）随机摸出一个球后，放回并搅匀，再随机摸出一个球，求两次都摸到相同颜色的小球的概率．（请结合树状图或列表解答）
参考答案
一、选择题（每题4分，共48分）
1、D
2、B
3、B
4、C
5、C
6、B
7、B
8、A
9、A
10、D
11、A
12、C
二、填空题（每题4分，共24分）
13、1
14、1
15、3
16、2π+2﹣4
17、6米.
18、
三、解答题（共78分）
19、（1）y2＝；（2）x＞2；（3）点A与两坐标轴围成的矩形OBAC的面积是1．
20、（1）这两年藏书的年均增长率是20%；（2）到2018年底中外古典名著的册数占藏书总量的10%．
21、（1）3t， 8-2t；（2）△BMN与△ABC相似时，t的值为s或s；（3）t的值为.
22、（1）y＝x2－4x＋2，（2）90°，（2）①，②m＝2或m＝或m＝1．
23、（1）60，10；（2）96°；（3）
24、（1）故答案为四；增大；；（2）．
25、（1）证明见解析；（2）．
26、（1）袋子中白球有2个；（2）见解析， .
移植总数
400
1500
3500
7000
9000
14000
成活数
369
1335
3203
6335
8073
12628
成活的频率
0923
0.890
0915
0.905
0.897
0.902