2023-2024学年湖北省黄冈市麻城市思源实验学校九年级数学第一学期期末统考模拟试题含答案

这是一份2023-2024学年湖北省黄冈市麻城市思源实验学校九年级数学第一学期期末统考模拟试题含答案，共9页。试卷主要包含了在平面直角坐标系中，点E，若点A等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题（每题4分，共48分）
1．已知，则的值是（ ）
A．B．C．D．
2．下列方程中，是一元二次方程的是（ ）
A．B．
C．D．
3．已知，是抛物线上两点，则正数（ ）
A．2B．4C．8D．16
4．在平面直角坐标系中，点E（﹣4，2），点F（﹣1，﹣1），以点O为位似中心，按比例1：2把△EFO缩小，则点E的对应点E的坐标为（ ）
A．（2，﹣1）或（﹣2，1）B．（8，﹣4）或（﹣8，4）C．（2，﹣1）D．（8，﹣4）
5．若点A（﹣2，y1），B（﹣1，y2），C（4，y3）都在二次函数的图象上，则下列结论正确的是（ ）
A．B．C．D．
6．在一个不透明的盒子中有20个除颜色外均相同的小球，每次摸球前先将盒中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复摸球试验后，发现摸到红球的频率稳定于0.3，由此可估计盒中红球的个数约为（ ）
A．3B．6C．7D．14
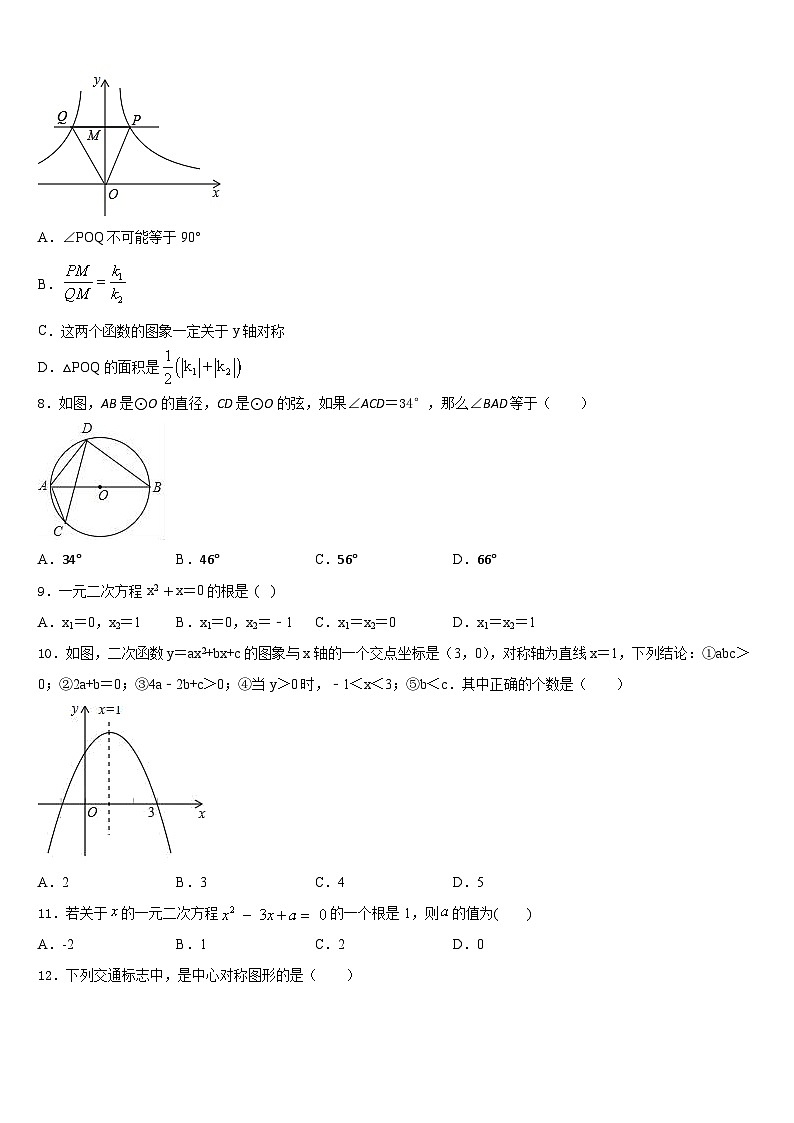
7．如图，若点M是y轴正半轴上的任意一点，过点M作PQ∥x轴，分别交函数y＝（y＞0）和y＝（y＞0）的图象于点P和Q，连接OP和OQ，则下列结论正确是（ ）
A．∠POQ不可能等于90°
B．
C．这两个函数的图象一定关于y轴对称
D．△POQ的面积是
8．如图，AB是⊙O的直径，CD是⊙O的弦，如果∠ACD＝34°，那么∠BAD等于（ ）
A．34°B．46°C．56°D．66°
9．一元二次方程 x2 ＋x＝0的根是 ( )
A．x1＝0，x2＝1B．x1＝0，x2＝﹣1C．x1＝x2＝0D．x1＝x2＝1
10．如图，二次函数y＝ax2+bx+c的图象与x轴的一个交点坐标是（3，0），对称轴为直线x＝1，下列结论：①abc＞0；②2a+b＝0；③4a﹣2b+c＞0；④当y＞0时，﹣1＜x＜3；⑤b＜c．其中正确的个数是（ ）
A．2B．3C．4D．5
11．若关于的一元二次方程的一个根是1，则的值为( )
A．-2B．1C．2D．0
12．下列交通标志中，是中心对称图形的是（ ）
A．B．C．D．
二、填空题（每题4分，共24分）
13．如图，已知的半径为2，内接于，，则__________．
14．我们定义一种新函数：形如（，且）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y=|x2-2x-3|的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为，和；②图象具有对称性，对称轴是直线；③当或时，函数值随值的增大而增大；④当或时，函数的最小值是0；⑤当时，函数的最大值是1．其中正确结论的个数是______.
15．如图，点是函数图象上的一点，连接，交函数的图象于点，点是轴上的一点，且，则的面积为_________.
16．如图，已知AB⊥BD，ED⊥BD，C是线段BD的中点，且AC⊥CE，ED=1，BD=4，那么AB= ．
17．当x_____时，|x﹣2|＝2﹣x．
18．抛物线y=（x﹣1）2+3的对称轴是直线_____．
三、解答题（共78分）
19．（8分）如图，已知：抛物线交x轴于A，C两点，交y轴于点B，且OB=2CO.
(1)求二次函数解析式；
(2)在二次函数图象位于x轴上方部分有两个动点M、N，且点N在点M的左侧，过M、N作x轴的垂线交x轴于点G、H两点，当四边形MNHG为矩形时，求该矩形周长的最大值；
(3) 抛物线对称轴上是否存在点P，使得△ABP为直角三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
20．（8分）粤东农批﹒2019球王故里五华马拉松赛于12月1日在广东五华举行，组委会为了做好运动员的保障工作，沿途设置了4个补给站，分别是：A（粤东农批）、B（奥体中心）、C（球王故里）和D（滨江中路），志愿者小明和小红都计划各自在这4个补给站中任意选择一个进行补给服务，每个补给站被选择的可能性相同．
（1）小明选择补给站C（球王故里）的概率是多少？
（2）用树状图或列表的方法，求小明和小红恰好选择同一个补给站的概率．
21．（8分）已知抛物线y＝ax2+bx+c经过点A(﹣2，0)，B(3，0)，与y轴负半轴交于点C，且OC＝OB．
（1）求抛物线的解析式；
（2）在y轴负半轴上存在一点D，使∠CBD＝∠ADC，求点D的坐标；
（3）点D关于直线BC的对称点为D′，将抛物线y＝ax2+bx+c向下平移h个单位，与线段DD′只有一个交点，直接写出h的取值范围．
22．（10分）某校为了深入学习社会主义核心价值观，对本校学生进行了一次相关知识的测试，随机抽取了部分学生的测试成绩进行统计（根据成绩分为、、、、五个组，表示测试成绩，组：；组：；组：；组：；组：），通过对测试成绩的分析，得到如图所示的两幅不完整的统计图，请你根据图中提供的信息解答以下问题：
（1）抽取的学生共有______人，请将两幅统计图补充完整；
（2）抽取的测试成绩的中位数落在______组内；
（3）本次测试成绩在80分以上（含80分）为优秀，若该校初三学生共有1200人，请估计该校初三测试成绩为优秀的学生有多少人？
23．（10分）某商店销售一种商品，每件成本8元，规定每件商品售价不低于成本，且不高于20元，经市场调查每天的销售量y（件）与每件售价x（元）满足一次函数关系，部分数据如下表：
（1）将上面的表格填充完整；
（2）设该商品每天的总利润为w元，求w与x之间的函数表达式；
（3）计算（2）中售价为多少元时，获得最大利润，最大利润是多少？
24．（10分）如图，Rt△ABC中，∠B＝90°，点D在边AC上，且DE⊥AC交BC于点E．
（1）求证：△CDE∽△CBA；
（2）若AB＝3，AC＝5，E是BC中点，求DE的长．
25．（12分）某学校为了增强学生体质，决定开设以下体育课外活动项目：A：篮球 B：乒乓球C：羽毛球 D：足球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：
（1）这次被调查的学生共有 人；
（2）请你将条形统计图（2）补充完整；
（3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）
26．（12分）（1）计算：
（2）解方程：．
参考答案
一、选择题（每题4分，共48分）
1、A
2、C
3、C
4、A
5、D
6、B
7、D
8、C
9、B
10、B
11、C
12、D
二、填空题（每题4分，共24分）
13、
14、1
15、4
16、4
17、≤2
18、x=1
三、解答题（共78分）
19、（1）y；（2）；（3）（1，-3）或（1，）或（1，1+）或（1，1-）
20、（1 ）；（2）
21、（1）y＝x2﹣x﹣3；（2）D(0，﹣6)；（3）3≤h≤1
22、（1）400，图详见解析；（2）B；（3）660人.
23、（1）见解析；（2）w＝﹣10x2+280x﹣1600；（3）售价为14元时，获得最大利润，最大利润是360元．
24、（1）证明见解析；（2）DE=．
25、解：（1）1．
（2）补全图形，如图所示：
（3）列表如下：
∵所有等可能的结果为12种，其中符合要求的只有2种，
∴恰好选中甲、乙两位同学的概率为．
26、（1）；（2）
售价x（元件）
10
11
12
13
14
x
销售量y（件）
100
90
80
70


甲
乙
丙
丁
甲
﹣﹣﹣
（乙，甲）
（丙，甲）
（丁，甲）
乙
（甲，乙）
﹣﹣﹣
（丙，乙）
（丁，乙）
丙
（甲，丙）
（乙，丙）
﹣﹣﹣
（丁，丙）
丁
（甲，丁）
（乙，丁）
（丙，丁）
﹣﹣﹣