2023-2024学年湖南省长沙市天心区部分学校九上数学期末达标检测试题含答案

这是一份2023-2024学年湖南省长沙市天心区部分学校九上数学期末达标检测试题含答案，共9页。试卷主要包含了下列计算正确的是，已知，则等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题（每题4分，共48分）
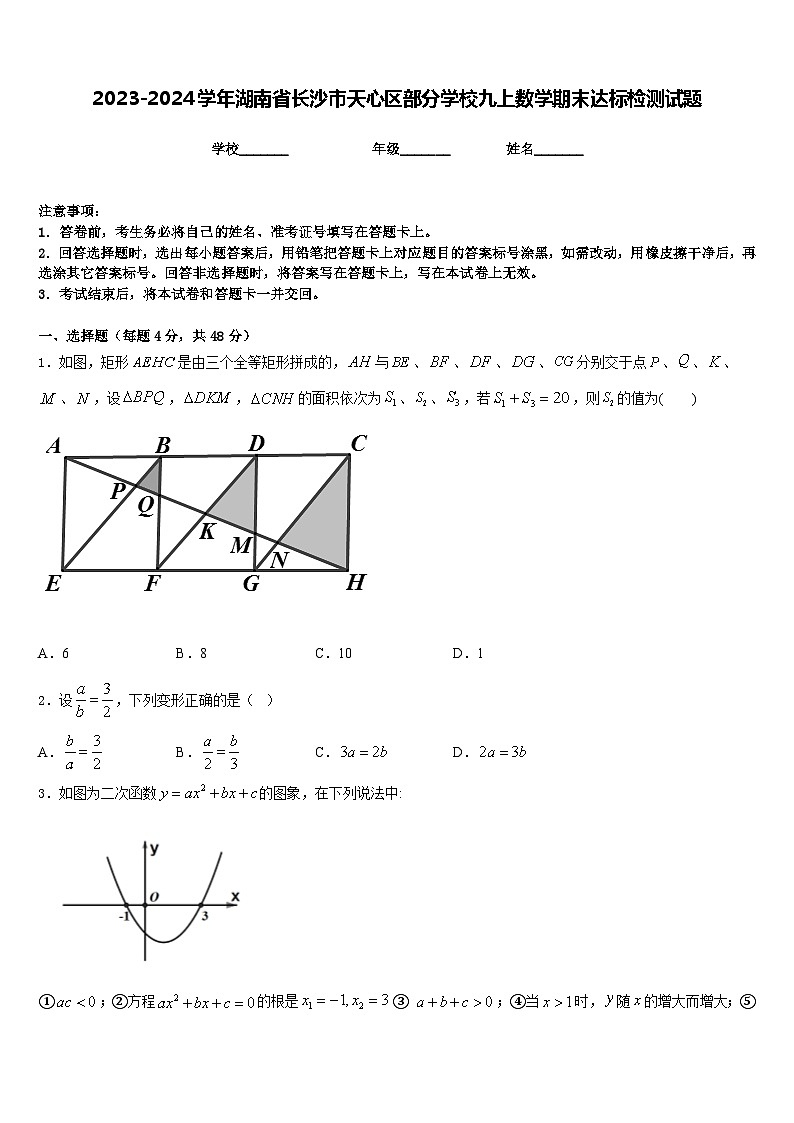
1．如图，矩形是由三个全等矩形拼成的，与、、、、分别交于点、、、、，设，，的面积依次为、、，若，则的值为( )
A．6B．8C．10D．1
2．设，下列变形正确的是（ ）
A．B．C．D．
3．如图为二次函数的图象，在下列说法中:
①；②方程的根是③ ；④当时，随的增大而增大；⑤；⑥，正确的说法有（ ）
A．B．C．D．
4．如图，将△ABC放在每个小正方形的边长都为1的网格中，点A，B，C均在格点上，则tanA的值是( )

A．B．C．2D．
5．⊙O的半径为5，圆心O到直线l的距离为3，下列位置关系正确的是( )
A．B．
C．D．
6．由若干个相同的小正方体搭成的一个几何体的俯视图和左视图如图所示，则搭成这个几何体的小正方体的个数最多有( )
A．5个B．6个C．7个D．8个
7．下列计算正确的是（ ）
A．B．C．÷D．
8．已知，则（ ）
A．1B．2C．4D．8
9．已知△ABC∽△A1B1C1，若△ABC与△A1B1C1的相似比为3：2，则△ABC与△A1B1C1的周长之比是（ ）
A．2：3B．9：4C．3：2D．4：9
10．将抛物线向左平移2个单位后所得到的抛物线为（ ）
A．B．
C．D．
11．已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点，其横坐标为1，则一次函数y=bx+ac的图象可能是（ ）
A． B． C． D．
12．如图，AB是半径为1的⊙O的直径，点C在⊙O上，∠CAB＝30°，D为劣弧CB的中点，点P是直径AB上一个动点，则PC+PD的最小值为（ ）
A．1B．2C．D．
二、填空题（每题4分，共24分）
13．若代数式5x－5与2x－9的值互为相反数，则x＝________.
14．反比例函数的图象经过点，，点是轴上一动点.当的值最小时，点的坐标是__________．
15．如果是从四个数中任取的一个数，那么关于的方程的根是负数的概率是________．
16．在△ABC中，∠C=90°，若AC=6，BC=8，则△ABC外接圆半径为________；
17．如图，折叠长方形的一边AD，使点D落在BC边的点F处，已知AB=8cm，BC=10cm，则EF=________
．
18．如图是一个用来盛爆米花的圆锥形纸杯，纸杯开口圆的直径长为，母线长为.在母线上的点处有一块爆米花残渣，且，一只蚂蚁从杯口的点处沿圆锥表面爬行到点，则此蚂蚁爬行的最短距离为____．
三、解答题（共78分）
19．（8分）已知，是一元二次方程的两个实数根，且，抛物线的图象经过点，，如图所示．
（1）求这个抛物线的解析式；
（2）设（1）中的抛物线与轴的另一个交点为，抛物线的顶点为，试求出点，的坐标，并判断的形状；
（3）点是直线上的一个动点（点不与点和点重合），过点作轴的垂线，交抛物线于点，点在直线上，距离点为个单位长度，设点的横坐标为，的面积为，求出与之间的函数关系式．
20．（8分）小明和小亮两人一起玩投掷一个普通正方体骰子的游戏．
（1）说出游戏中必然事件，不可能事件和随机事件各一个；
（2）如果两个骰子上的点数之积为奇数，小明胜，否则小亮胜，你认为这个游戏公平吗？如果不公平，谁获胜的可能性较大？请说明理由．请你为他们设计一个公平的游戏规则．
21．（8分）附加题,已知：矩形，，动点从点开始向点运动，动点速度为每秒1个单位，以为对称轴，把折叠，所得与矩形重叠部分面积为，运动时间为秒.
（1）当运动到第几秒时点恰好落在上；
（2）求关于的关系式，以及的取值范围；
（3）在第几秒时重叠部分面积是矩形面积的；
（4）连接，以为对称轴，将作轴对称变换，得到，当为何值时，点在同一直线上？
22．（10分）如图，▱ABCD中，连接AC，AB⊥AC，tanB＝，E、F分别是BC，AD上的点，且CE＝AF，连接EF交AC与点G．
（1）求证：G为AC中点；
（2）若EF⊥BC，延长EF交BA的延长线于H，若FH＝4，求AG的长．
23．（10分）如图，直线y＝x﹣3与x轴、y轴分别交于点B、点C，经过B、C两点的抛物线y＝﹣x2+mx+n与x轴的另一个交点为A，顶点为P．
(1)求3m+n的值；
(2)在该抛物线的对称轴上是否存在点Q，使以C，P，Q为顶点的三角形为等腰三角形？若存在，求出有符合条件的点Q的坐标；若不存在，请说明理由．
(3)将该抛物线在x轴上方的部分沿x轴向下翻折，图象的其余部分保持不变，翻折后的图象与原图象x轴下方的部分组成一个“M“形状的新图象，若直线y＝x+b与该“M”形状的图象部分恰好有三个公共点，求b的值．
24．（10分）如图， 相交于点，连结．
(1)求证: ；
(2)直接回答与是不是位似图形?
(3)若，求的长．
25．（12分）如图，在菱形中，点在对角线上，延长交于点.
（1）求证：；
（2）已知点在边上，请以为边，用尺规作一个与相似，并使得点在上.（只须作出一个，保留作图痕迹，不写作法）
26．（12分）已知在平面直角坐标系中，抛物线与x轴相交于点A，B，与y轴相交于点C，直线y=x+4经过A，C两点，
（1）求抛物线的表达式；
（2）如果点P，Q在抛物线上（P点在对称轴左边），且PQ∥AO，PQ=2AO，求P，Q的坐标；
（3）动点M在直线y=x+4上，且△ABC与△COM相似，求点M的坐标．
参考答案
一、选择题（每题4分，共48分）
1、B
2、D
3、D
4、D
5、B
6、D
7、C
8、C
9、C
10、D
11、B
12、C
二、填空题（每题4分，共24分）
13、2
14、
15、
16、5
17、5cm
18、
三、解答题（共78分）
19、（1）；（2），，是直角三角形；（3）当时，，当或时，．
20、（1）详见解析；（2）不公平，规则详见解析．
21、（1）第2秒时；（2）；（3）第4秒时；（4）=1或4
22、（1）见解析；（2）
23、 (1)9；(2)点Q的坐标为(2，1﹣2)或(2，1+2)或(2，﹣)或(2，﹣7)；(3)b＝﹣3或﹣．
24、（1）详见解析；（2）不是；（3）
25、（1）详见解析；（2）详见解析；
26、（1）（2）P点坐标（﹣5，﹣），Q点坐标（3，﹣）（3）M点的坐标为（﹣，），（﹣3，1）