2023-2024学年雅安市重点中学数学九上期末质量检测模拟试题含答案

这是一份2023-2024学年雅安市重点中学数学九上期末质量检测模拟试题含答案，共8页。试卷主要包含了已知关于x的方程，若关于x的一元二次方程等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题（每题4分，共48分）
1．如图，线段CD两个端点的坐标分别为C（4，4）、D（6，2），以原点O为位似中心，在第一象限内将线段CD缩小为线段AB，若点B的坐标为（3，1），则点A的坐标为（ ）
A．（0，3）B．（1，2）C．（2，2）D．（2，1）
2．如图，四边形ABCD是正方形，以BC为底边向正方形外部作等腰直角三角形BCE，连接AE，分别交BD，BC于点F，G，则下列结论：①△AFB∽△ABE；②△ADF∽△GCE；③CG=3BG；④AF=EF，其中正确的有（ ）.
A．①③B．②④C．①②D．③④
3．若二次函数y＝-x2+px+q的图像经过A（，n）、B（0，y1）、C（，n）、D（，y2）、E（，y3），则y1、y2、y3的大小关系是（ ）
A．y3＜y2＜y1B．y3＜y1＜y2C．y1＜y2＜y3D．y2＜y3＜y1
4．已知关于x的方程（m+4）x2+2x﹣3m＝0是一元二次方程，则m的取值范围是（ ）
A．m＜﹣4B．m≠0C．m≠﹣4D．m＞﹣4
5．若关于x的一元二次方程（k﹣1）x2+2x﹣2=0有两个不相等的实数根，则k的取值范围是（ ）
A．k＞B．k≥C．k＞且k≠1D．k≥且k≠1
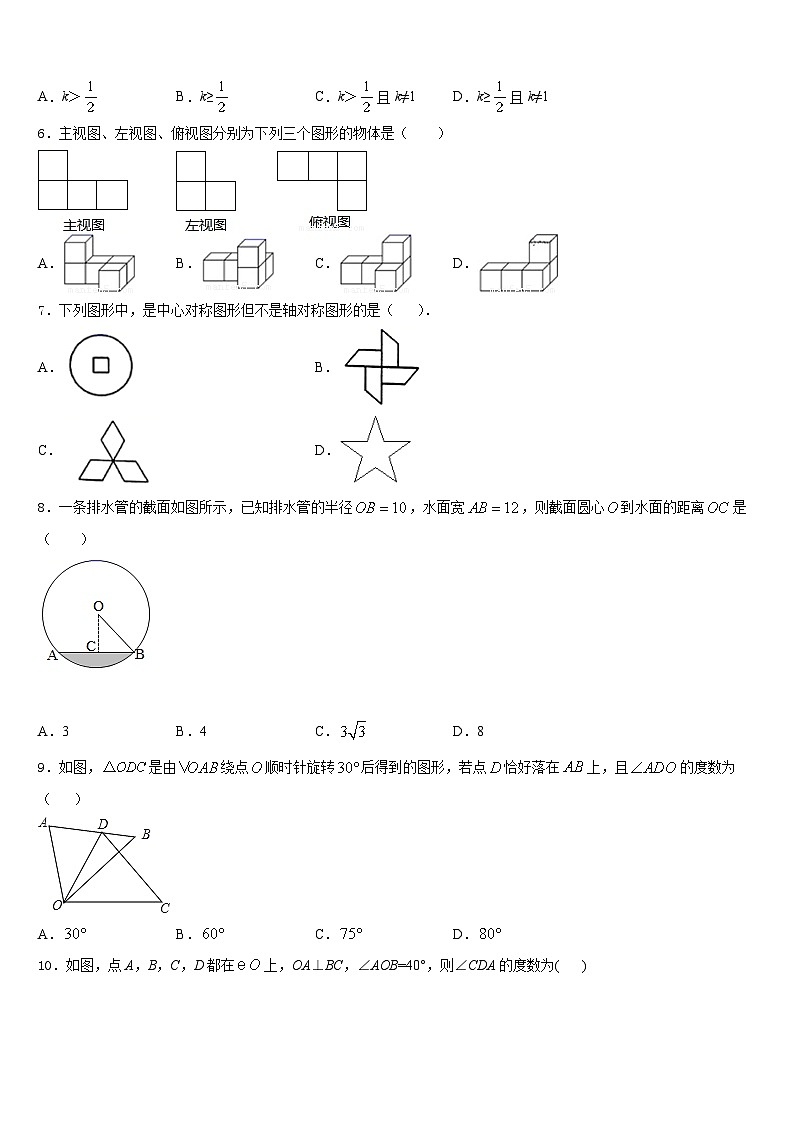
6．主视图、左视图、俯视图分别为下列三个图形的物体是（ ）
A．B．C．D．
7．下列图形中，是中心对称图形但不是轴对称图形的是（ ）．
A．B．
C．D．
8．一条排水管的截面如图所示，已知排水管的半径，水面宽，则截面圆心到水面的距离是（ ）
A．3B．4C．D．8
9．如图，是由绕点顺时针旋转后得到的图形，若点恰好落在上，且的度数为（ ）
A．B．C．D．
10．如图，点A，B，C，D都在上，OA⊥BC，∠AOB=40°，则∠CDA的度数为( )
A．40°B．30°C．20°D．15°
11．如图，四边形ABCD中，∠A＝90°，AB＝12，AD＝5，点M、N分别为线段BC、AB上的动点（含端点，但点M不与点B重合），点E、F分别为DM、MN的中点，则EF长度的可能为（ ）
A．2B．5C．7D．9
12．已知关于x的方程x2－kx－6＝0的一个根为x＝－3，则实数k的值为( )
A．1B．－1C．2D．－2
二、填空题（每题4分，共24分）
13．直角三角形的直角边和斜边分别是和，则此三角形的外接圆半径长为__________．
14．如图，在平面直角坐标系中，点A的坐标是（20，0），点B的坐标是（16，0），点C、D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，则点C的坐标为_____．
15．如图，在平面直角坐标系中，点A、B的坐标分别是（0，2）、（4，0），点P是直线y=2x+2上的一动点，当以P为圆心，PO为半径的圆与△AOB的一条边所在直线相切时，点P的坐标为__________．
16．当_________时，关于的一元二次方程有两个实数根.
17．如图，有一张直径为1.2米的圆桌，其高度为0.8米，同时有一盏灯距地面2米，圆桌在水平地面上的影子是，∥，和是光线，建立如图所示的平面直角坐标系，其中点的坐标是．那么点的坐标是_________．
18．把抛物线向上平移2个单位，所得的抛物线的解析式是__________.
三、解答题（共78分）
19．（8分）如图所示，已知AB为⊙O的直径，CD是弦，且AB⊥CD于点E，连接AC、OC、BC
（1）求证：∠ACO＝∠BCD；
（2）若EB＝8cm，CD＝24cm，求⊙O的面积．（结果保留π）
20．（8分）满洲里市某楼盘准备以每平方米5000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望．为了加快资金周转，房地产开发商对价格经过两次下调后，决定以每平方米4050元的均价开盘销售．
（1）求平均每次下调的百分率；
（2）某人准备以开盘均价购买一套100平方米的房子．开发商还给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，送两年物业管理费，物业管理费是每平方米每月1.5元，请问哪种方案更优惠？
21．（8分）如图，已知等边△ABC，AB＝1．以AB为直径的半圆与BC边交于点D，过点D作DF⊥AC，垂足为F，过点F作FG⊥AB，垂足为G，连结GD．
(1)求证：DF是⊙O的切线；
(2)求FG的长；
(3)求△FDG的面积．
22．（10分）如图，在中，.以为直径的与交于点，与交于点，点在边的延长线上，且.
（1）试说明是的切线；
（2）过点作，垂足为.若，，求的半径；
（3）连接，设的面积为，的面积为，若，，求的长.
23．（10分）如图，在△ABC中，AB＝AC，点D为BC的中点，经过AD两点的圆分别与AB，AC交于点E、F，连接DE，DF．
（1）求证：DE＝DF；
（2）求证：以线段BE+CF，BD，DC为边围成的三角形与△ABC相似，
24．（10分）《庄子·天下》：“一尺之棰，日取其半，万世不竭．”意思是说：一尺长的木棍，每天截掉一半，永远也截不完．我国智慧的古代人在两千多年前就有了数学极限思想，今天我们运用此数学思想研究下列问题．
（规律探索）
（1）如图1所示的是边长为1的正方形，将它剪掉一半，则S阴影1＝1－＝
如图2，在图1的基础上，将阴影部分再裁剪掉—半，则S阴影2＝1－－()2 ＝____；
同种操作，如图3，S阴影3＝1－－()2－()3 ＝__________；
如图4，S阴影4＝1－－()2－()3－()4 ＝___________；
……若同种地操作n次，则S阴影n＝1－－()2－()3－…－()n ＝_________．
于是归纳得到：+()2+()3+…+()n =_________．
（理论推导）
（2）阅读材料：求1+2+22+23+24+…+22015+22016的值．
解：设S=1+2+22+23+24+…+22015+22016，①
将①×2得：2S=2+22+23+24+…+22016+22017，②
由②-①得：2S—S=22017—1，即=22017-1．
即1+2+22+23+24+…+22015+22016＝22017-1
根据上述材料，试求出+()2+()3+…+()n 的表达式，写出推导过程．
（规律应用）
（3）比较＋＋＋…… __________1（填“”、“”或“=”）
25．（12分）已知：在△ABC中，点D、点E分别在边AB、AC上，且DE // BC，BE平分∠ABC．
（1）求证：BD=DE；
（2）若AB=10，AD=4，求BC的长．
26．（12分）如图，在下列10×10的网格中，横、纵坐标均为整点的数叫做格点，例如A（2，1）、B（5，4）、C（1，8）都是格点．
（1）直接写出△ABC的面积；
（2）将△ABC绕点B逆时针旋转90°得到△A1BC1，在网格中画出△A1BC1；
（3）在图中画出线段EF，使它同时满足以下条件：①点E在△ABC内；②点E，F都是格点；③EF三等分BC；④EF＝．请写出点E，F的坐标．
参考答案
一、选择题（每题4分，共48分）
1、C
2、B
3、A
4、C
5、C
6、A
7、B
8、D
9、C
10、C
11、B
12、B
二、填空题（每题4分，共24分）
13、1
14、（2，6）
15、（0，2），（﹣1，0），（﹣，1）．
16、
17、
18、
三、解答题（共78分）
19、（1）见解析；（2）169π（cm2）．
20、 (1)、10%；(2)、方案一优惠
21、（1）详见解析；（2）；（3）
22、（1）详见解析；（2）3；（3）.
23、（1）详见解析；（2）详见解析
24、（1）；；；()n；1 - ()n ；（2）+()2+()3+…+()n = 1-()n，推导过程见解析；（3）=
25、（1）见解析；（2）15
26、（1）12;（2）见解析;（3）E（2，4），F（7，8）.