云南省昆明市五华区2023-2024学年九年级数学第一学期期末统考模拟试题含答案

这是一份云南省昆明市五华区2023-2024学年九年级数学第一学期期末统考模拟试题含答案，共9页。
学校_______ 年级_______ 姓名_______
请考生注意：
1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。
一、选择题（每题4分，共48分）
1．甲袋中装有形状、大小与质地都相同的红球3个，乙袋中装有形状、大小与质地都相同的红球2个，黄球1个，下列事件为随机事件的是（ ）
A．从甲袋中随机摸出1个球，是黄球
B．从甲袋中随机摸出1个球，是红球
C．从乙袋中随机摸出1个球，是红球或黄球
D．从乙袋中随机摸出1个球，是黄球
2．已知当x＞0时，反比例函数y＝的函数值随自变量的增大而减小，此时关于x的方程x2﹣2（k+1）x+k2﹣1＝0的根的情况为（ ）
A．有两个相等的实数根B．没有实数根
C．有两个不相等的实数根D．无法确定
3．如图，在平面直角坐标系中，与轴相切，直线被截得的弦长为，若点的坐标为，则的值为（ ）
A．B．C．D．
4．如图的的网格图，A、B、C、D、O都在格点上，点O是（ ）
A．的外心B．的外心C．的内心D．的内心
5．一元二次方程x2－8x－1=0配方后为( )
A．(x－4)2=17B．(x＋4)2=15
C．(x＋4)2=17D．(x－4)2=17或(x＋4)2=17
6．程大位是我国明朝商人，珠算发明家．他60岁时完成的《直指算法统宗》是东方古代数学名著，详述了传统的珠算规则，确立了算盘用法．对书中某一问题改编如下：意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个正好分完，大和尚共分得（ ）个馒头
A．25B．72C．75D．90
7．二次函数图象上部分点的坐标对应值列表如下：
则该函数图象的对称轴是（ ）
A．直线x＝﹣3B．直线x＝﹣2C．直线x＝﹣1D．直线x＝0
8．一元二次方程的一个根为，则的值为（ ）
A．1B．2C．3D．4
9．在一个不透明的布袋中装有9个白球和若干个黑球，它们除颜色不同外，其余均相同。若从中随机摸出一个球，摸到白球的概率是，则黑球的个数为（ ）
A．3B．12C．18D．27
10．若关于x的一元二次方程有实数根，则实数k的取值范围为
A．，且B．，且
C．D．
11．方程的根是( )
A．B．
C．D．
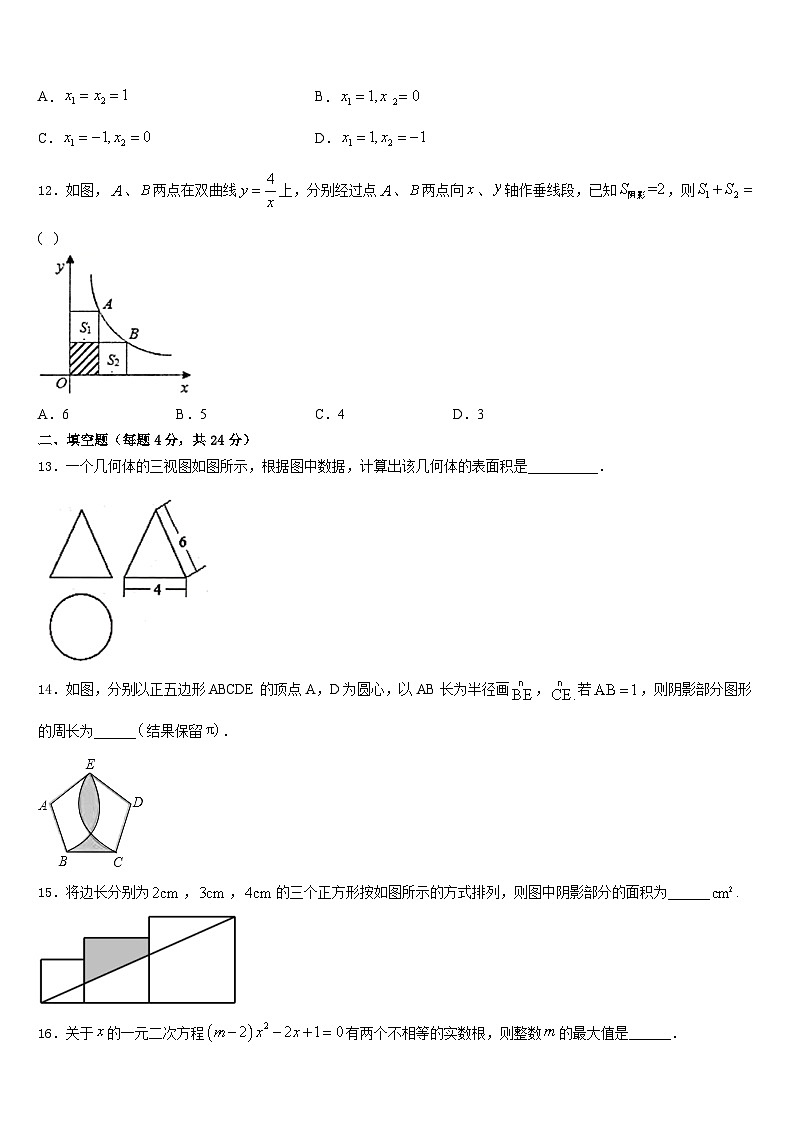
12．如图，、两点在双曲线上，分别经过点、两点向、轴作垂线段，已知，则( )
A．6B．5C．4D．3
二、填空题（每题4分，共24分）
13．一个几何体的三视图如图所示，根据图中数据，计算出该几何体的表面积是__________．
14．如图，分别以正五边形ABCDE的顶点A，D为圆心，以AB长为半径画，若，则阴影部分图形的周长为______结果保留．
15．将边长分别为，，的三个正方形按如图所示的方式排列，则图中阴影部分的面积为______.
16．关于的一元二次方程有两个不相等的实数根，则整数的最大值是______．
17．某工厂1月份的产值为50000元，3月份的产值达到72000元，这两个月的产值平均月增长的百分率是多少？
18．如图，在四边形ABCD中，∠BAD=∠CDA=90°，AB=1，CD=2，过A，B，D三点的⊙O分别交BC，CD于点E，M，下列结论：
①DM=CM；②弧AB=弧EM；③⊙O的直径为2；④AE=AD．
其中正确的结论有______（填序号）．
三、解答题（共78分）
19．（8分）如图，在矩形ABCD中，AB＝6，BC＝4，动点Q在边AB上，连接CQ，将△BQC沿CQ所在的直线对折得到△CQN，延长QN交直线CD于点M．
（1）求证：MC＝MQ
（2）当BQ＝1时，求DM的长；
（3）过点D作DE⊥CQ，垂足为点E，直线QN与直线DE交于点F，且，求BQ的长．
20．（8分）阅读以下材料，并按要求完成相应地任务：
莱昂哈德·欧拉(Lenhard Euler)是瑞士数学家，在数学上经常见到以他的名字命名的重要常数，公式和定理，下面是欧拉发现的一个定理：在△ABC中，R和r分别为外接圆和内切圆的半径，O和I分别为其外心和内心，则.
如图1，⊙O和⊙I分别是△ABC的外接圆和内切圆，⊙I与AB相切分于点F，设⊙O的半径为R，⊙I的半径为r，外心O（三角形三边垂直平分线的交点）与内心I（三角形三条角平分线的交点）之间的距离OI＝d，则有d2＝R2﹣2Rr．
下面是该定理的证明过程（部分）：
延长AI交⊙O于点D，过点I作⊙O的直径MN，连接DM，AN.
∵∠D=∠N，∠DMI=∠NAI(同弧所对的圆周角相等)，
∴△MDI∽△ANI，
∴，
∴①，
如图2，在图1(隐去MD，AN)的基础上作⊙O的直径DE，连接BE，BD，BI，IF，
∵DE是⊙O的直径，∴∠DBE=90°，
∵⊙I与AB相切于点F，∴∠AFI=90°，
∴∠DBE=∠IFA，
∵∠BAD=∠E(同弧所对圆周角相等)，
∴△AIF∽△EDB，
∴，∴②，
任务：(1)观察发现：， (用含R，d的代数式表示)；
(2)请判断BD和ID的数量关系，并说明理由；
(3)请观察式子①和式子②，并利用任务(1)，(2)的结论，按照上面的证明思路，完成该定理证明的剩余部分；
(4)应用：若△ABC的外接圆的半径为5cm，内切圆的半径为2cm，则△ABC的外心与内心之间的距离为 cm.

21．（8分）如图是一个横断面为抛物线形状的拱桥，当水面宽（AB）为4m时，拱顶（拱桥洞的最高点）离水面2m．当水面下降1m时，求水面的宽度增加了多少？
22．（10分）等腰中，，作的外接圆⊙O.
（1）如图1，点为上一点（不与A、B重合），连接AD、CD、AO，记与的交点为.
①设，若，请用含与的式子表示；
②当时，若，求的长；
（2）如图2，点为上一点（不与B、C重合），当BC=AB，AP=8时，设，求为何值时，有最大值？并请直接写出此时⊙O的半径．
23．（10分）如图，AG是∠PAQ的平分线，点E在AQ上，以AE为直径的⊙0交AG于点D，过点D作AP的垂线，垂足为点C，交AQ于点B．
（1）求证：直线BC是⊙O的切线；
（2）若⊙O的半径为6，AC=2CD，求BD的长
24．（10分）一玩具厂去年生产某种玩具，成本为元/件，出厂价为元/件，年销售量为万件．今年计划通过适当增加成本来提高产品档次，以拓展市场．若今年这种玩具每件的成本比去年成本增加倍，今年这种玩具每件的出厂价比去年出厂价相应提高倍，则预计今年年销售量将比去年年销售量增加倍（本题中）．
用含的代数式表示，今年生产的这种玩具每件的成本为________元，今年生产的这种玩具每件的出厂价为________元．
求今年这种玩具的每件利润元与之间的函数关系式．
设今年这种玩具的年销售利润为万元，求当为何值时，今年的年销售利润最大？最大年销售利润是多少万元？
注：年销售利润（每件玩具的出厂价-每件玩具的成本）年销售量．
25．（12分）如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E为⊙O上一点，过点E作直线DC分别交AM，BN于点D，C，且CB=CE．
（1）求证：DA=DE；
（2）若AB=6，CD=4，求图中阴影部分的面积．
26．（12分）如图，△ABC是一块锐角三角形余料，边BC=120 mm，高AD=80mm，要把它加工成矩形零件PQMN，使矩形PQMN的边QM在BC上，其余两个项点P，N分别在AB，AC上．
（1）当矩形的边PN=PQ时，求此时矩形零件PQMN的面积；
（2）求这个矩形零件PQMN面积S的最大值．
参考答案
一、选择题（每题4分，共48分）
1、D
2、C
3、B
4、B
5、A
6、C
7、B
8、B
9、C
10、A
11、A
12、C
二、填空题（每题4分，共24分）
13、
14、+1．
15、
16、1
17、20%
18、①②④
三、解答题（共78分）
19、（1）见解析；（2）2.1；（3）或2
20、 (1)R-d；(2)BD=ID，理由见解析；(3)见解析；(4).
21、水面宽度增加了（2﹣4）米
22、（1）①；②；（2）PB=5时，S有最大值，此时⊙O的半径是.
23、（1）证明见详解；（2）8.
24、10＋7x 12＋6x
25、（1）证明见解析；（2）
26、（1）矩形零件PQMN的面积为2304mm2;（2）这个矩形零件PQMN面积S的最大值是2400mm2.
x
…
﹣3
﹣2
﹣1
0
1
…
y
…
﹣3
﹣2
﹣3
﹣6
﹣11
…