云南省曲靖市沾益县2023-2024学年九上数学期末学业质量监测模拟试题含答案

这是一份云南省曲靖市沾益县2023-2024学年九上数学期末学业质量监测模拟试题含答案，共8页。试卷主要包含了考生要认真填写考场号和座位序号，抛物线y＝﹣等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。
一、选择题（每题4分，共48分）
1．用圆心角为120°，半径为6cm的扇形纸片卷成一个圆锥形无底纸帽（如图所示），则这个纸帽的高是（ ）
A．cmB．3cmC．4cmD．4cm
2．下列事件中，属于必然事件的是（ ）
A．2020年的除夕是晴天B．太阳从东边升起
C．打开电视正在播放新闻联播D．在一个都是白球的盒子里，摸到红球
3．一个袋中有黑球个，白球若干，小明从袋中随机一次摸出个球，记下其黑球的数目，再把它们放回，搅匀后重复上述过程次，发现共有黑球个．由此估计袋中的白球个数是( )
A．40个B．38个C．36个D．34个
4．如图，四点在⊙上，. 则的度数为（ ）
A．B．C．D．
5．已知二次函数的与的部分对应值如表：
下列结论：抛物线的开口向上；②抛物线的对称轴为直线；③当时，；④抛物线与轴的两个交点间的距离是；⑤若是抛物线上两点，则，其中正确的个数是（ ）
A．B．C．D．
6．二次函数的图象与y轴的交点坐标是（ ）
A．（0，1）B．（1，0）C．（－1，0）D．（0，－1）
7．抛物线y＝﹣（x+2）2+5的顶点坐标是（ ）
A．（2，5）B．（﹣2，5）C．（﹣2，﹣5）D．（2，﹣5）
8．某企业五月份的利润是25万元，预计七月份的利润将达到49万元．设平均月增长率为x，根据题意可列方程是（ ）
A．25(1+ x %)2=49B．25(1+x)2=49
C．25(1+ x2) =49D．25(1- x)2=49
9．如图，矩形EFGO的两边在坐标轴上，点O为平面直角坐标系的原点，以y轴上的某一点为位似中心，作位似图形ABCD，且点B，F的坐标分别为（﹣4，4），（2，1），则位似中心的坐标为（ ）
A．（0，3）B．（0，2.5）C．（0，2）D．（0，1.5）
10．如图，AB 是⊙O的直径，弦CD⊥AB于点M，若CD＝8 cm，MB＝2 cm，则直径AB的长为（ ）
A．9 cmB．10 cmC．11 cmD．12 cm
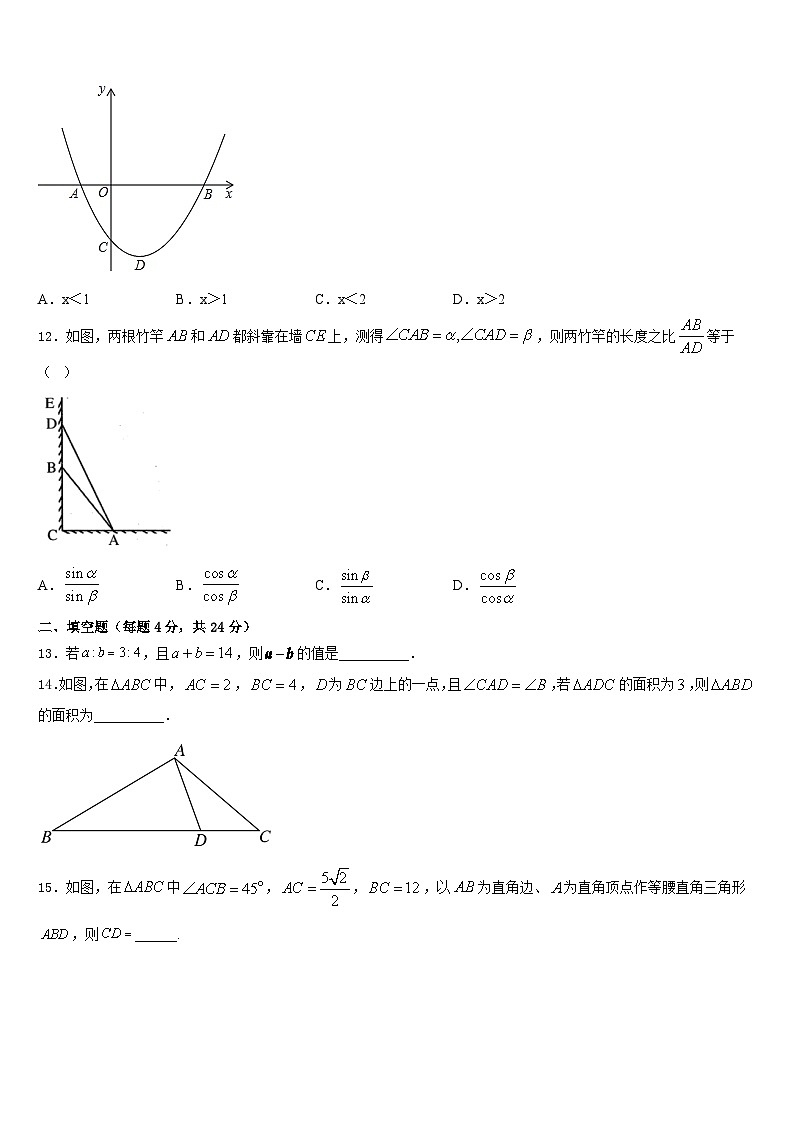
11．如图，二次函数y＝ax2+bx+c（a＞0）的图象与x轴的交点A、B的横坐标分别为﹣1和3，则函数值y随x值的增大而减小时，x的取值范围是（ ）
A．x＜1B．x＞1C．x＜2D．x＞2
12．如图，两根竹竿和都斜靠在墙上，测得，则两竹竿的长度之比等于（ ）
A．B．C．D．
二、填空题（每题4分，共24分）
13．若，且，则的值是__________．
14．如图，在中，，，为边上的一点，且，若的面积为，则的面积为__________．
15．如图，在中，，，以为直角边、为直角顶点作等腰直角三角形，则______.
16．如果一元二次方程有两个相等的实数根，那么是实数的取值为________．
17．二次函数的图象与轴交于两点（点在点的左侧），与轴交于点，作直线，将直线下方的二次函数图象沿直线向上翻折，与其它剩余部分组成一个组合图象，若线段与组合图象有两个交点，则的取值范围为_____．
18．如图，在△ABC中，点DE分别在ABAC边上，DE∥BC，∠ACD=∠B，若AD=2BD，BC=6.则线段CD的长为______
三、解答题（共78分）
19．（8分）在平面直角坐标系xOy中，已知抛物线G：y＝ax2﹣2ax+4（a≠0）．
（1）当a＝1时，
①抛物线G的对称轴为x＝ ；
②若在抛物线G上有两点（2，y1），（m，y2），且y2＞y1，则m的取值范围是 ；
（2）抛物线G的对称轴与x轴交于点M，点M与点A关于y轴对称，将点M向右平移3个单位得到点B，若抛物线G与线段AB恰有一个公共点，结合图象，求a的取值范围．
20．（8分）（1）计算：tan31°sin61°＋cs231°－tan45°
（2）解方程：x2﹣2x﹣1=1．
21．（8分）已知关于x的一元二次方程2x2＋(2k＋1)x＋k＝1．
（1）求证：方程总有两个实数根；
（2）若该方程有一个根是正数，求k的取值范围．
22．（10分）如图，△ABC的坐标依次为（﹣1，3）、（﹣4，1）、（﹣2，1），将△ABC绕原点O顺时针旋转180°得到△A1B1C1．
（1）画出△A1B1C1；
（2）求在此变换过程中，点A到达A1的路径长．
23．（10分）甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情．
(1)若从甲、乙两医院支援的医护人员中分别随机选1名，则所选的2名医护人员性别相同的概率是 ；
(2)若从支援的4名医护人员中随机选2名，用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率．
24．（10分）如图，在平面直角坐标系中，抛物线的图象与x轴交于，B两点，与y轴交于点，对称轴与x轴交于点H.
（1）求抛物线的函数表达式
（2）直线与y轴交于点E，与抛物线交于点P,Q（点P在y轴左侧，点Q 在y轴右侧），连接CP，CQ，若的面积为，求点P，Q的坐标.
（3）在（2）的条件下，连接AC交PQ于G，在对称轴上是否存在一点K，连接GK，将线段GK绕点G逆时针旋转90°，使点K恰好落在抛物线上，若存在，请直接写出点K的坐标不存在，请说明理由.

25．（12分）（1）计算：．
（2）用适当方法解方程：
（3）用配方法解方程：
26．（12分）在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=xm.
（1）若花园的面积为192m2, 求x的值；
（2）若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），求花园面积S的最大值.
参考答案
一、选择题（每题4分，共48分）
1、C
2、B
3、D
4、B
5、B
6、D
7、B
8、B
9、C
10、B
11、A
12、D
二、填空题（每题4分，共24分）
13、-2
14、1
15、1
16、
17、或
18、
三、解答题（共78分）
19、（1）①1；②m＞2或m＜0；（2）﹣＜a≤﹣或a＝1．
20、（1）；（2）x=1
21、（1）见解析；（2）
22、（1）画图见解析；（2）点A到达A1的路径长为π．
23、（1）；（2）
24、（1）；（2）；（3）
25、（1）3;(2) x1=,x2=；(3) x1＝1+，x2＝1−．
26、（1）12m或16m；（2）195.