人教版数学七年级下册 第9章《不等式与不等式组》复习课件+测试卷

这是一份人教版数学七年级下册 第9章《不等式与不等式组》复习课件+测试卷，共21页。

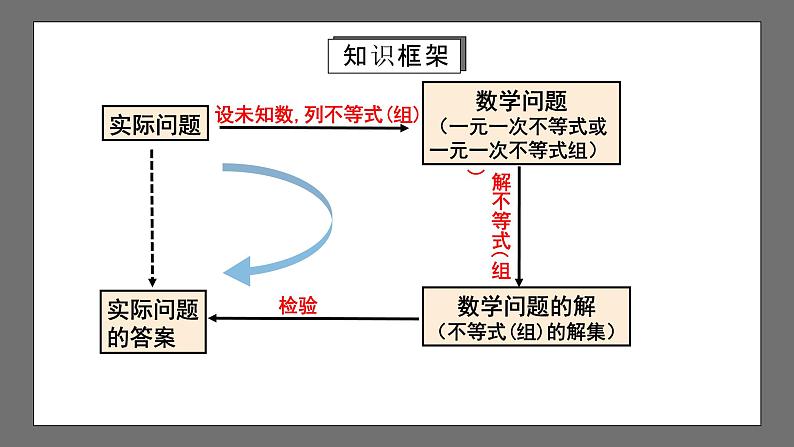
第9章不等式与不等式组复习与小结1.能够根据具体问题中的大小关系了解不等式的意义，并探索不等式的基本性质.2.会解简单一元一次不等式，并能在数轴上表示出解集.3.会解由两个一元一次不等式组成的不等式组，并会用数轴确定解集.4.能够根据具体问题中的数量关系，列出一元一次不等式（组），解决简单的实际问题.复习目标实际问题数学问题（一元一次不等式或一元一次不等式组）数学问题的解（不等式(组)的解集）实际问题的答案 设未知数,列不等式(组)知识框架知识点一 不等式及其解集像①和②这样用符号“＜”或“＞”表示大小关系的式子，叫做不等式. 像a+2≠a-2这样用符号“≠”表示不等关系的式子也是不等式.不等式: 有些不等式中不含未知数,例如 3＜4,-1＞-2.有些不等式中含有未知数,例如①和②式中字母x表示未知数.知识梳理知识点一 不等式及其解集使不等式成立的未知数的值叫不等式的解.不等式的解：例如80和78，是不等式 的解，而75和72，不是不等式 的解. 一般的，一个含有未知数的不等式的所有的解，组成这个不等式的解集. 求不等式的解集的过程叫解不等式.知识梳理知识点二 不等式的性质不等式的性质1： 不等式两边加(或减)同一个数(或式子) ，不等号的方向不变.如果a＞b，那么a±c＞b±c.不等式的性质2： 不等式两边都乘(或除以)同一个正数，不等号的方向不变．知识梳理知识点二 不等式的性质不等式的性质3： 不等式两边都乘（或除以）同一个负数，不等号的方向改变.知识梳理知识点三 一元一次不等式及解一元一次不等式含有一个未知数，未知数次数是１的不等式，叫做一元一次不等式．一元一次不等式：解一元一次不等式：则要根据不等式的性质，将不等式逐步化为x＜a或x＞a的形式.步骤：去分母、去括号、移项、合并同类项、将未知数的系数化为1．知识梳理知识点四 一元一次不等式组及其解集 类似于方程组，把这两个不等式合起来，组成一个一元一次不等式组， 记作30x＞1200， ①30x＜1500. ②知识梳理知识点四 一元一次不等式组及其解集由不等式①，解得x＞40.由不等式②，解得x＜50.把不等式①和②的解集在数轴上表示出来(如下图).∴不等式组的解集为 40＜x＜50.知识梳理知识点四 一元一次不等式组及其解集 一般地，几个不等式的解集的公共部分，叫做由它们所组成的不等式组的解集. 解不等式组就是求它的解集.知识梳理解一元一次不等式组步骤：1.求出不等式组中各不等式的解集.2.将各不等式的解决在数轴上表示出来.3.在数轴上找出各不等式解集的公共部分，这个公共部分就是不等式组的解集.知识点四 一元一次不等式组及其解集知识梳理知识点四 一元一次不等式组及其解集知识梳理A课堂检测课堂检测3.不等式组 的解集在数轴上表示正确的是（　　） A． B． C． D．C课堂检测4.不等式组 的非负整数解有（ ） A．4个 B．5个 C．6个 D．7个B课堂检测5.解不等式组： ．解：解不等式①得x＞2， 解不等式②得x＜5．∴不等式组的解集是2＜x＜5．课堂检测解：设他可以买x支钢笔,则笔记本为（8-x)个，由题意，得4.5x+3（8-x）≤30解得 x≤4∴X=4或3或2或1∵X为正整数，答:小兰有4种购买方案： ①4支钢笔和4本笔记本,② 3支钢笔和5本笔记,③ 2支钢笔和6本笔记, ④ 1支钢笔和7本笔记.6.小兰准备用30元买钢笔和笔记本，已知一支钢笔4.5元，一本笔记本3元，如果她钢笔和笔记本共买了8件，每一种至少买一件,则她有多少种购买方案？课堂检测7.一堆玩具分给若干个小朋友，若每人分3件，则剩余4件；若前面每人分4件，则最后一人得到的玩具不足3件，求小朋友的人数与玩具数.解：设小朋友总共有x人，由此可得不等式组由此可得5＜x≤8，因为x是整数，∴x=6，7，8.答：小朋友有6人，玩具有22件；或小朋友有7人，玩具有25件；或小朋友有8人，玩具有28件.课堂检测课程结束