安徽省合肥市部分学校2023-2024学年九上数学期末综合测试试题含答案

这是一份安徽省合肥市部分学校2023-2024学年九上数学期末综合测试试题含答案，共8页。试卷主要包含了答题时请按要求用笔等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题（每题4分，共48分）
1．如图，△ABC内接于圆，D是BC上一点，将∠B沿AD翻折，B点正好落在圆点E处，若∠C＝50°，则∠BAE的度数是（ ）
A．40°B．50°C．80°D．90°
2．如图，在平面直角坐标系中，点A的坐标为（0，4），△OAB沿x轴向右平移后得到△O'A'B'，A的对应点A'是直线上一点，则点B与其对应点B'间的距离为（ ）
A．3B．4C．5D．6
3．某市从2017年开始大力发展“竹文化”旅游产业．据统计，该市2017年“竹文化”旅游收入约为2亿元．预计2019“竹文化”旅游收入达到2.88亿元，据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为（ ）
A．2%B．4.4%C．20%D．44%
4．《九章算术》是我国古代第一部自成体系的数学专著，书中记载：“今有圆材，埋在壁中，不知大小，以锯锯之，深两寸，锯道长八寸，问径几何？”译为：“今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深2寸（ED＝2寸），锯道长8寸”，问这块圆形木材的直径是多少？”如图所示，请根据所学知识计算圆形木材的直径AC是（ ）
A．5寸B．8寸C．10寸D．12寸
5．如图，在▱ABCD中，F为BC的中点，延长AD至E，使DE：AD＝1：3，连接FF交DC于点G，则DG：CG＝（ ）
A．1：2B．2：3C．3：4D．2：5
6．已知关于的一元二次方程两实数根为、，则（ ）
A．3B．﹣3C．1D．﹣1
7．如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点（﹣3，0），其对称轴为直线x＝﹣，结合图象分析下列结论：①abc＞0；②3a+c＞0；③当x＜0时，y随x的增大而增大：④若m，n（m＜n）为方程a（x+3）（x﹣2）+3＝0的两个根，则m＜﹣3且n＞2；⑤＜0，其中正确的结论有（ ）
A．2个B．3个C．4个D．5个
8．点在反比例函数y＝的图象上，则k的值是（ ）
A．1B．3C．﹣1D．﹣3
9．如图，交于点，切于点，点在上. 若，则为（ ）
A．B．C．D．
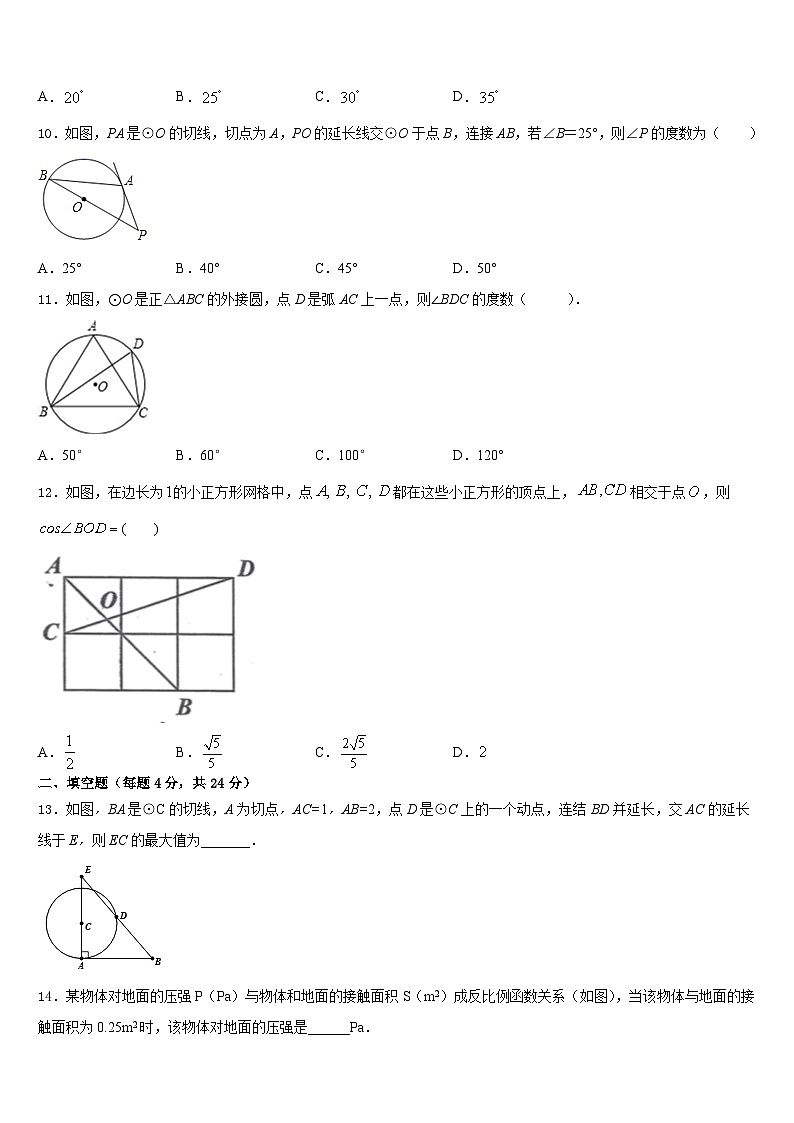
10．如图，PA是⊙O的切线，切点为A，PO的延长线交⊙O于点B，连接AB，若∠B＝25°，则∠P的度数为（ ）
A．25°B．40°C．45°D．50°
11．如图，⊙O是正△ABC的外接圆，点D是弧AC上一点，则∠BDC的度数（ ）．
A．50°B．60°C．100°D．120°
12．如图，在边长为的小正方形网格中，点都在这些小正方形的顶点上，相交于点，则( )
A．B．C．D．
二、填空题（每题4分，共24分）
13．如图，BA是⊙C的切线，A为切点，AC=1，AB=2，点D是⊙C上的一个动点，连结BD并延长，交AC的延长线于E，则EC的最大值为_______．
14．某物体对地面的压强P（Pa）与物体和地面的接触面积S（m2）成反比例函数关系（如图），当该物体与地面的接触面积为0.25m2时，该物体对地面的压强是______Pa．
15．如图，的半径长为，与相切于点，交半径的延长线于点，长为，，垂足为，则图中阴影部分的面积为_______．
16．在一个不透明的布袋中装有黄、白两种颜色的球共40个，除颜色外其他都相同，小王通过多次摸球试验后发现，摸到黄球的频率稳定在0.35左右，则布袋中黄球可能有_________个
17．点P(4，﹣6)关于原点对称的点的坐标是_____．
18．如图，的顶点均在上，，则的半径为_________．
三、解答题（共78分）
19．（8分）如图，在△ABC中，AB=AC，tan∠ACB=2，D在△ABC内部，且AD=CD，∠ADC=90°，连接BD，若△BCD的面积为10，则AD的长为多少？
20．（8分）如图，是由两个长方体组合而成的一个立体图形的主视图和左视图，根据图中所标尺寸(单位: )．
(1)直接写出上下两个长方休的长、宽、商分别是多少:
(2)求这个立体图形的体积．
21．（8分）如图，在的正方形网格中，网线的交点称为格点，点，，都是格点．已知每个小正方形的边长为1．
（1）画出的外接圆，并直接写出的半径是多少．
（2）连结，在网络中画出一个格点，使得是直角三角形，且点在上．
22．（10分）如图，在平面直角坐标系中，双曲线和直线y=kx+b交于A，B两点，点A的坐标为（﹣3，2），BC⊥y轴于点C，且OC=6BC．
（1）求双曲线和直线的解析式；
（2）直接写出不等式的解集．
23．（10分）化简并求值： ，其中m满足m2-m-2=0.
24．（10分）如图，有一个斜坡，坡顶离地面的高度为20米，坡面的坡度为，求坡面的长度.
25．（12分）已知：如图，在四边形ABCD中，AB∥CD，对角线AC、BD交于点E，点F在边AB上，连接CF交线段BE于点G，CG2=GE•GD．
（1）求证：∠ACF=∠ABD；
（2）连接EF，求证：EF•CG=EG•CB．
26．（12分）如图，点是线段上的任意一点(点不与点重合)，分别以为边在直线的同侧作等边三角形和等边三角形，与相交于点，与相交于点．
(1)求证: ；
(2)求证: ；
(3)若的长为12cm，当点在线段上移动时，是否存在这样的一点，使线段的长度最长?若存在,请确定点的位置并求出的长；若不存在，请说明理由．
参考答案
一、选择题（每题4分，共48分）
1、C
2、C
3、C
4、C
5、B
6、A
7、C
8、B
9、B
10、B
11、B
12、B
二、填空题（每题4分，共24分）
13、
14、1
15、
16、14
17、 (﹣4，6)
18、1
三、解答题（共78分）
19、5
20、（1）立体图形下面的长方体的长、宽、高分别为；上面的长方体的长、宽、高分别为；（2）这个立体图形的体积为．
21、（1）作图见解析，半径为；（2）作图见解析
22、（1）双曲线的解析式为，直线的解析式为y=﹣2x﹣4；（2）﹣3＜x＜0或x＞1.
23、，原式=
24、米
25、（1）证明见解析；（2）证明见解析．
26、 (1)见解析；(2) 见解析；(1) 存在,请确定C点的位置见解析，MN=1．