山东省莱城区刘仲莹中学2023-2024学年九年级数学第一学期期末统考模拟试题含答案

这是一份山东省莱城区刘仲莹中学2023-2024学年九年级数学第一学期期末统考模拟试题含答案，共8页。试卷主要包含了考生要认真填写考场号和座位序号等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。
一、选择题（每题4分，共48分）
1．抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝－1，与x轴的一个交点在(－3，0)和(－2，0)之间，其部分图象如图，则下列结论：①4ac－b2＜0；②2a－b＝0；③a＋b＋c＜0；④点(x1，y1)，(x2，y2)在抛物线上，若x1＜x2，则y1＜y2 .正确结论的个数是( )
A．1B．2C．3D．4
2．如图，将绕着点按顺时针方向旋转，点落在位置，点落在位置，若，则的度数是 （ ）
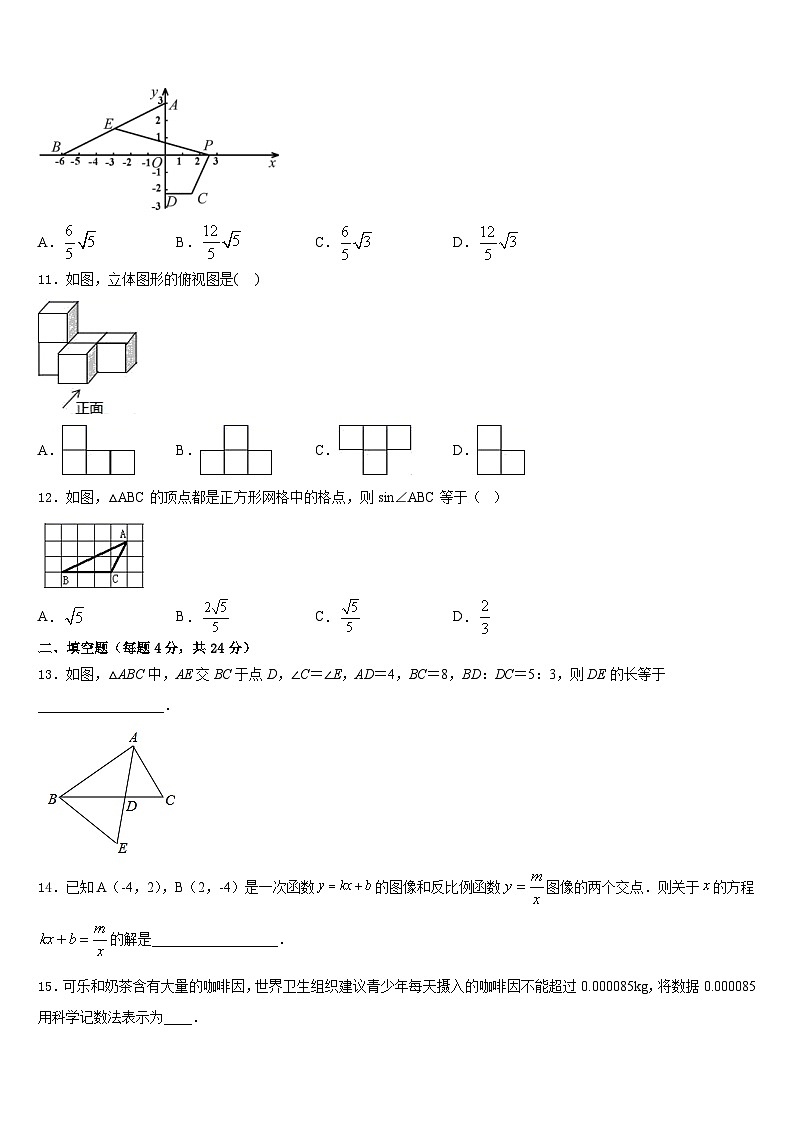
A．B．C．D．
3．如图，函数的图象与轴的一个交点坐标为(3,0)，则另一交点的横坐标为（ ）
A．﹣4B．﹣3C．﹣2D．﹣1
4．关于x的一元二次方程有实数根，则整数a的最大值是（ ）
A．2B．1C．0D．－1
5．下列关于反比例函数,结论正确的是（ ）
A．图象必经过
B．图象在二，四象限内
C．在每个象限内，随的增大而减小
D．当时，则
6．抛物线y＝x2﹣4x+1与y轴交点的坐标是（ ）
A．（0，1）B．（1，O）C．（0，﹣3）D．（0，2）
7．下列几何体中，同一个几何体的主视图与左视图不同的是（ ）
A．B．C．D．
8．二次函数的图象如右图所示，若，，则（ ）
A．，B．，C．，D．，
9．一元二次方程 x2 ＋x＝0的根是 ( )
A．x1＝0，x2＝1B．x1＝0，x2＝﹣1C．x1＝x2＝0D．x1＝x2＝1
10．在平面直角坐标系中，点，，过第四象限内一动点作轴的垂线，垂足为，且，点、分别在线段和轴上运动，则的最小值是（ ）
A．B．C．D．
11．如图，立体图形的俯视图是( )
A．B．C．D．
12．如图，△ABC的顶点都是正方形网格中的格点，则sin∠ABC等于（ ）
A．B．C．D．
二、填空题（每题4分，共24分）
13．如图，△ABC中，AE交BC于点D，∠C＝∠E，AD＝4，BC＝8，BD：DC＝5：3，则DE的长等于__________________．
14．已知A（-4，2），B（2，-4）是一次函数的图像和反比例函数图像的两个交点．则关于的方程的解是__________________．
15．可乐和奶茶含有大量的咖啡因，世界卫生组织建议青少年每天摄入的咖啡因不能超过0.000085kg，将数据0.000085用科学记数法表示为____．
16．设m是一元二次方程x2﹣x﹣2019＝0的一个根，则m2﹣m+1的值为___．
17．把配方成的形式为__________．
18．如图，六边形ABCDEF是正六边形，曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”，其中弧FK1、弧K1K2、弧K2K3、弧K3K4、弧K4K5、弧K5K6、…的圆心依次按点A、B、C、D、E、F循环，其弧长分别为l1、l2、l3、l4、l5、l6、…．当AB＝1时，l3=________，l2019＝_________．
三、解答题（共78分）
19．（8分）如图，△ABC内接于⊙O，AB=AC=10，BC=12，点E是弧BC的中点.
(1)过点E作BC的平行线交AB的延长线于点D，求证：DE是⊙O的切线.
(2)点F是弧AC的中点，求EF的长.
20．（8分）如图，抛物线y=x2+bx+c与直线y=x+3交于A，B两点，交x轴于C、D两点，连接AC、BC，已知A（0，3），C（﹣3，0）．
（1）求抛物线的解析式；
（2）在抛物线对称轴l上找一点M，使|MB﹣MD|的值最大，并求出这个最大值；
（3）点P为y轴右侧抛物线上一动点，连接PA，过点P作PQ⊥PA交y轴于点Q，问：是否存在点P使得以A，P，Q为顶点的三角形与△ABC相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．
21．（8分）一位橄榄球选手掷球时，橄榄球从出手开始行进的高度与水平距离之间的关系如图所示，已知橄榄球在距离原点时，达到最大高度，橄榄球在距离原点13米处落地，请根据所给条件解决下面问题：
（1）求出与之间的函数关系式；
（2）求运动员出手时橄榄球的高度．
22．（10分）如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，其边长为2，点A，点C分别在轴，轴的正半轴上．函数的图象与CB交于点D，函数（为常数，）的图象经过点D，与AB交于点E，与函数的图象在第三象限内交于点F，连接AF、EF．
（1）求函数的表达式，并直接写出E、F两点的坐标．
（2）求△AEF的面积．
23．（10分）某中学对全校学生进行文明礼仪知识测试，为了解测试结果，随机抽取部分学生的成绩进行分析，将成绩分为三个等级：不合格、一般、优秀，并绘制成如下两幅统计图（不完整）．
请你根据图中所给的信息解答下列问题：
（1）请将以上两幅统计图补充完整；
（2）若“一般”和“优秀”均被视为达标成绩，则该校被抽取的学生中有 人达标；
（3）若该校学生有1200人，请你估计此次测试中，全校达标的学生有多少人？
24．（10分）如图，，是的两条弦，点分别在，上，且，是的中点．
求证:（1）．
（2）过作于点．当，时，求的半径．
25．（12分）如图，是⊙的直径，，是的中点，连接并延长到点，使.连接交⊙于点，连接.
（1）求证：直线是⊙的切线；
（2）若，求⊙的半径.
26．（12分）如图①，矩形中，，，将绕点从处开始按顺时针方向旋转，交边（或）于点，交边（或）于点.当旋转至处时，的旋转随即停止.
（1）特殊情形：如图②，发现当过点时，也恰好过点，此时是否与相似？并说明理由；
（2）类比探究：如图③，在旋转过程中，的值是否为定值？若是，请求出该定值；若不是，请说明理由；
（3）拓展延伸：设时，的面积为，试用含的代数式表示；
①在旋转过程中，若时，求对应的的面积；
②在旋转过程中，当的面积为4.2时，求对应的的值.
参考答案
一、选择题（每题4分，共48分）
1、C
2、C
3、D
4、C
5、B
6、A
7、A
8、A
9、B
10、B
11、C
12、C
二、填空题（每题4分，共24分）
13、
14、x1=-4，x1=1
15、8.1×10-1
16、2020.
17、
18、π 673π
三、解答题（共78分）
19、（1）见解析；（2）
20、（1）抛物线的解析式是y=x2+x+3；（2）|MB﹣MD|取最大值为；（3）存在点P（1，6）．
21、（1）（2）
22、（1），E（2，1），F（-1，-2）；（2）．
23、（1）详见解析；（2）1；（3）10
24、（1）见解析；（2）
25、（1）见解析;（2）.
26、（1）相似；（2）定值，；（3）①2，②.