2023-2024学年黄石市重点中学数学九上期末学业水平测试试题含答案

这是一份2023-2024学年黄石市重点中学数学九上期末学业水平测试试题含答案，共8页。试卷主要包含了考生要认真填写考场号和座位序号，已知，满足，则的值是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。
一、选择题（每题4分，共48分）
1．下列图象能表示y是x的函数的是（ ）
A．B．
C．D．
2．如图，已知Rt△ABC中，∠C＝90°，BC=3,AC=4，
则sinA的值为（ ）．
A．B．
C．D．
3．如图,在矩形ABCD中,AD=10,AB=6,E为BC上一点,DE平分∠AEC,则CE的长为( )
A．1B．2
C．3D．4
4．已知，满足，则的值是（ ）．
A．16B．C．8D．
5．若二次函数的图象如图，与x轴的一个交点为（1，0），则下列各式中不成立的是（ ）
A．B．C．D．
6．一件衣服225元，连续两次降价x%后售价为144元，则x＝（ ）
A．0.2B．2C．8D．20
7．如图，AC是电杆AB的一根拉线，现测得BC=6米，∠ABC=90°，∠ACB=52°，则拉线AC的长为（ ）米.
A． B． C． D．
8．作⊙O的内接正六边形ABCDEF，甲、乙两人的作法分别是：
甲：第一步：在⊙O上任取一点A，从点A开始，以⊙O的半径为半径，在⊙O上依次截取点B，C，D，E，F. 第二步：依次连接这六个点.
乙：第一步：任作一直径AD．第二步：分别作OA，OD的中垂线与⊙O相交，交点从点A开始，依次为点B，C，E，F. 第三步：依次连接这六个点.
对于甲、乙两人的作法，可判断( )
A．甲正确，乙错误B．甲、乙均错误
C．甲错误，乙正确D．甲、乙均正确
9．下列关于x 的一元二次方程，有两个不相等的实数根的方程的是( )
A．x2＋1＝0B．x2＋2x＋1＝0C．x2＋2x＋3＝0D．x2＋2x－3＝0
10．下列图形中，既是中心对称图形，又是轴对称图形的是( )
A．B．C．D．
11．在同一时刻，身高1.6m的小强在阳光下的影长为0.8m，一棵大树的影长为4.8m，则树的高度为（ ）
A．4.8mB．6.4mC．9.6mD．10m
12．下列图形中不是位似图形的是
A．B．C．D．
二、填空题（每题4分，共24分）
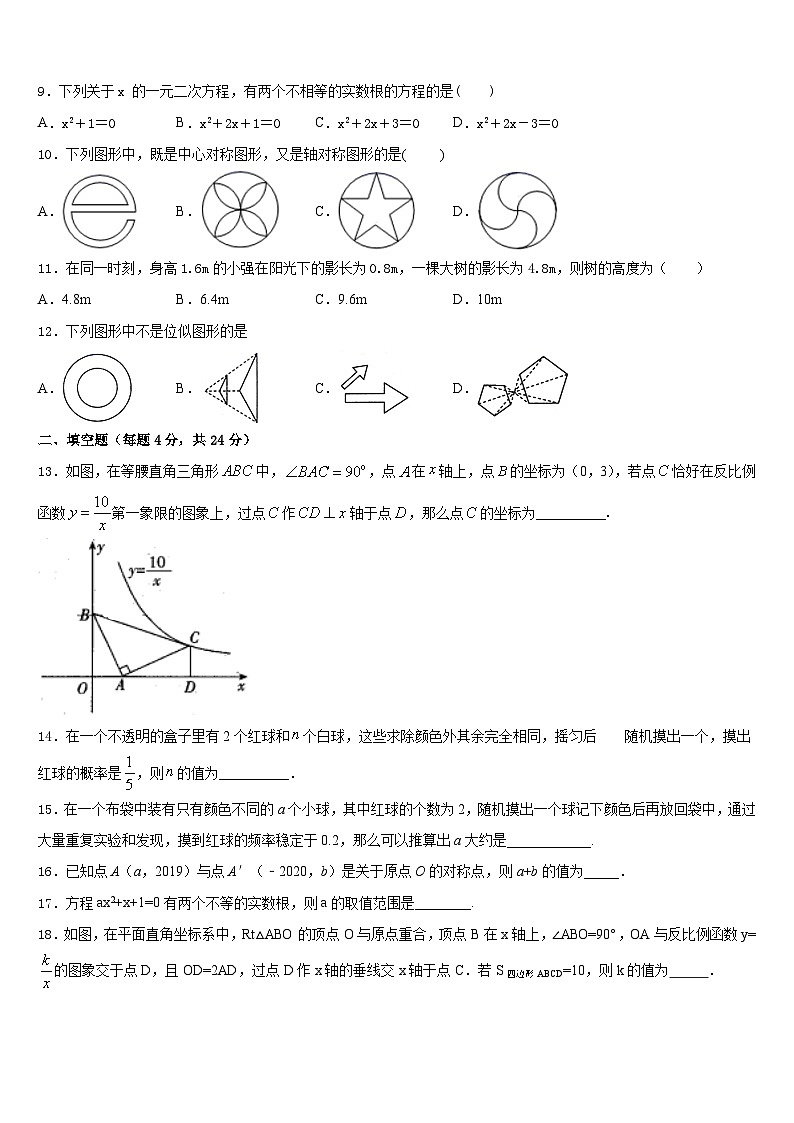
13．如图，在等腰直角三角形中，，点在轴上，点的坐标为（0，3），若点恰好在反比例函数第一象限的图象上，过点作轴于点，那么点的坐标为__________．
14．在一个不透明的盒子里有2个红球和个白球，这些求除颜色外其余完全相同，摇匀后 随机摸出一个，摸出红球的概率是，则的值为__________．
15．在一个布袋中装有只有颜色不同的a个小球，其中红球的个数为2，随机摸出一个球记下颜色后再放回袋中，通过大量重复实验和发现，摸到红球的频率稳定于0.2，那么可以推算出a大约是____________.
16．已知点A（a，2019）与点A′（﹣2020，b）是关于原点O的对称点，则a+b的值为_____．
17．方程ax2+x+1=0 有两个不等的实数根，则a的取值范围是________.
18．如图，在平面直角坐标系中，Rt△ABO的顶点O与原点重合，顶点B在x轴上，∠ABO=90°，OA与反比例函数y=的图象交于点D，且OD=2AD，过点D作x轴的垂线交x轴于点C．若S四边形ABCD=10，则k的值为 ．
三、解答题（共78分）
19．（8分）解一元二次方程：x2+4x﹣5＝1．
20．（8分）如图，已知直线AB经过点（0，4），与抛物线y=x2交于A，B两点，其中点A的横坐标是．
(1）求这条直线的函数关系式及点B的坐标．
(2）在x轴上是否存在点C，使得△ABC是直角三角形？若存在，求出点C的坐标，若不存在请说明理由．
(3）过线段AB上一点P，作PM∥x轴，交抛物线于点M，点M在第一象限，点N（0，1），当点M的横坐标为何值时，MN+3MP的长度最大？最大值是多少？
21．（8分）如图1,在平面内,不在同一条直线上的三点同在以点为圆心的圆上,且的平分线交于点,连接,．
（1）求证：；
（2）如图2,过点作,垂足为点,作,垂足为点,延长交于点,连接．若,请判断直线与的位置关系,并说明理由．
22．（10分）在平面直角坐标系中，已知P（,）,R（,）两点，且，，若过点P作轴的平行线，过点R作轴的平行线，两平行线交于一点S，连接PR，则称△PRS为点P，R，S的“坐标轴三角形”.若过点R作轴的平行线，过点P作轴的平行线，两平行线交于一点，连接PR，则称△RP为点R，P，的“坐标轴三角形”.右图为点P，R，S的“坐标轴三角形”的示意图.
（1）已知点A（0，4），点B（3，0）,若△ABC是点A，B，C的“坐标轴三角形”，则点C的坐标为 ；
（2）已知点D（2，1），点E（e，4），若点D，E，F的“坐标轴三角形”的面积为3，求e的值.
（3）若的半径为，点M（，4），若在上存在一点N，使得点N，M，G的“坐标轴三角形”为等腰三角形，求的取值范围.
23．（10分）如图，AB为⊙O直径，点D为AB下方⊙O上一点，点C为弧ABD中点，连接CD，CA．
（1）若∠ABD＝α，求∠BDC（用α表示）；
（2）过点C作CE⊥AB于H，交AD于E，∠CAD＝β，求∠ACE（用β表示）；
（3）在（2）的条件下，若OH＝5，AD＝24，求线段DE的长．
24．（10分）一件商品进价100元，标价160元时，每天可售出200件，根据市场调研，每降价1元，每天可多售出10件，反之，价格每提高1元，每天少售出10件．以160元为基准，标价提高m元后，对应的利润为w元．
（1）求w与m之间的关系式；
（2）要想获得利润7000元，标价应为多少元？
25．（12分）2018年非洲猪瘟疫情暴发后，专家预测，2019年我市猪肉售价将逐月上涨，每千克猪肉的售价y1（元）与月份x（1≤x≤12，且x为整数）之间满足一次函数关系，如下表所示．每千克猪肉的成本y2（元）与月份x（1≤x≤12，且x为整数）之间满足二次函数关系，且3月份每千克猪肉的成本全年最低，为9元，如图所示．
（1）求y1与x之间的函数关系式．
（2）求y2与x之间的函数关系式．
（3）设销售每千克猪肉所获得的利润为w（元），求w与x之间的函数关系式，哪个月份销售每千克猪肉所第获得的利润最大？最大利润是多少元？
26．（12分）如图，反比例函数y＝（x＞0）和一次函数y＝mx+n的图象过格点（网格线的交点）B、P．
（1）求反比例函数和一次函数的解析式；
（2）观察图象，直接写出一次函数值大于反比例函数值时x的取值范围是： ．
（3）在图中用直尺和2B铅笔画出两个矩形（不写画法），要求每个矩形均需满足下列两个条件：
①四个顶点均在格点上，且其中两个顶点分别是点O，点P；
②矩形的面积等于k的值．
参考答案
一、选择题（每题4分，共48分）
1、D
2、C
3、B
4、A
5、B
6、D
7、C
8、D
9、D
10、B
11、C
12、C
二、填空题（每题4分，共24分）
13、（5,2）
14、1
15、1
16、1．
17、且a≠0
18、﹣1
三、解答题（共78分）
19、x2＝﹣5，x2＝2．
20、（1）直线y=x+4，点B的坐标为（8，16）；（2）点C的坐标为（﹣，0），（0，0），（6，0），（32，0）；（3）当M的横坐标为6时，MN+3PM的长度的最大值是1．
21、（1）见解析 （2）见解析
22、（1）（3，4）；（2）或；（3）m的取值范围是或.
23、（1）∠BDC=α；（2）∠ACE=β；（3）DE=．
24、（1）w＝﹣1m2﹣400m+12000（0≤m≤20）；（2）标价应为11元或170元．
25、（1）y1＝2x+6；（2）y2＝x2﹣x+；（3）w＝﹣x2+x﹣，1月份销售每千克猪肉所第获得的利润最大，最大利润是11元1．
26、（1）y＝，y＝﹣+3；（2）2＜x＜1；（3）见解析
月份x
…
3
4
5
6
…
售价y1/元
…
12
14
16
18
…