初中数学北师大版八年级上册5 三角形的内角和定理教学课件ppt

这是一份初中数学北师大版八年级上册5 三角形的内角和定理教学课件ppt，共14页。PPT课件主要包含了学习目标，合作探究，典例精析，课堂练习，x70，x60，x30，x50，课堂小结等内容，欢迎下载使用。

1．证明三角形内角和定理，并能运用这些定理解决简单的问题．2．经历探索与证明的过程，进一步发展推理能力．3．在一题多解、一题多变中，积累解决几何问题的经验，提升解决问题的能力．
你还有什么方法可以达到同样的效果？
参考答案：可以用“两直线平行，同旁内角互补”来说明.可以通过作辅助线实现移动的效果，例如延长BC到点D，过点C作射线CE∥BA，这样就相当于把∠A移到了∠1的位置，∠B移到了∠2的位置.这里的CD、CE称为辅助线，辅助线通常画成虚线。
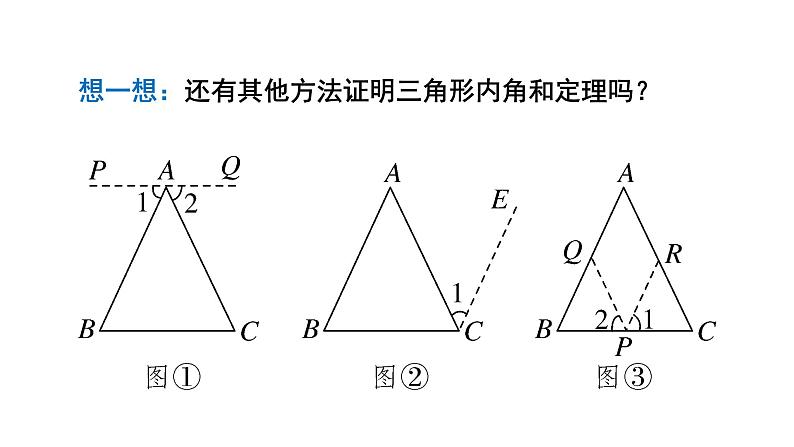
想一想：还有其他方法证明三角形内角和定理吗？
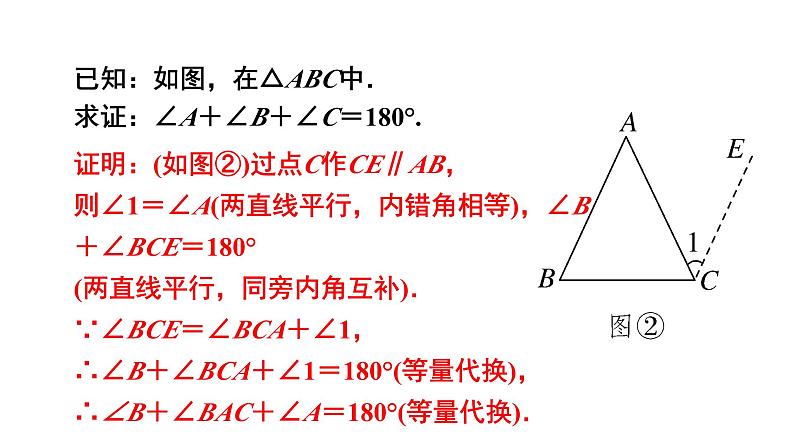
已知：如图，在△ABC中．求证：∠A＋∠B＋∠C＝180°.
证明：(如图①)过点A作PQ∥BC，则∠1＝∠B，∠2＝∠C(两直线平行，内错角相等)．∵∠1＋∠BAC＋∠2＝180°(平角的定义)∴∠B＋∠BAC＋∠C＝180°(等量代换)．
证明：(如图②)过点C作CE∥AB，则∠1＝∠A(两直线平行，内错角相等)，∠B＋∠BCE＝180°(两直线平行，同旁内角互补)．∵∠BCE＝∠BCA＋∠1，∴∠B＋∠BCA＋∠1＝180°(等量代换)，∴∠B＋∠BAC＋∠A＝180°(等量代换)．
证明：(如图③)过BC边上的一点P作QP∥AC，RP∥AB，交AB于Q，交AC于R，则∠1＝∠B，∠2＝∠C(两直线平行，同位角相等)．∠A＝∠BQP＝∠QPR(两直线平行，同位角相等，内错角相等)．∵∠1＋∠2＋∠QPR＝180°(平角的定义)，∴∠A＋∠B＋∠C＝180°(等量代换)．
例 如图，在△ABC中，∠B=38°，∠C=62°，AD是△ABC的角平分线，求∠ADB的度数.
1.求出下列各图中的x值．
2.如图，则∠1+∠2+∠3+∠4=___________ .
3.在△ABC中，如果∠A＝ ∠B＝ ∠C，求∠A、∠B、∠C分别等于多少度？
4.如图，在△ABC中，∠B=42°，∠C=78°，AD平分∠BAC．求∠ADC的度数.
解：∵∠B=42°，∠C=78°，∴∠BAC=180°-∠B-∠C=60°.∵AD平分∠BAC，∴∠CAD= ∠BAC=30°，∴∠ADC=180°-∠B-∠CAD=72°.
1．三角形内角和等于180°.2．定理的证明3．定理的应用