

2023-2024学年广东省清远市英德市七年级(上)学期期末数学试题(含解析)
展开
这是一份2023-2024学年广东省清远市英德市七年级(上)学期期末数学试题(含解析),共15页。试卷主要包含了选择题,填空题,解答题一,解答题二,解答题三等内容,欢迎下载使用。
一、选择题:共10小题,每小题3分,共30分.
1.如图是我国航天载人火箭的实物图,可以看成的立体图形为( )
A.棱锥与棱柱的组合体B.圆锥与圆柱的组合体
C.棱锥与圆柱的组合体D.圆锥与棱柱的组合体
2.下列选项中,不具有相反意义的量的是( )
A.买入20台电脑与卖出20台电脑B.水位上升与水位下降
C.减少与增高D.向东走和向西走
3.如图,数轴上的点表示的数可能是( )
A.B.C.D.
4.生长在良好的自然条件下的清远特色麻鸡,是中国十大名鸡之一,也是粤北山区客家民系世代选育的“斗鸡”王.为宣传这一特产,某班学生制作了一个正方体玩具,其展开图如图所示,原正方体中的“清”字所在的面相对的面上标的字应是( )
A.特B.色C.麻D.鸡
5.单项式的次数是( )
A.-1B.1C.2D.3
6.要调查下面的问题,适合采用普查方式的是( )
A.动车质检员对零部件的检查B.调查某批次方便面的防腐剂含量
C.调查北江某河段的水污染情况D.调查某市初中学生一天的睡眠时长
7.七边形的对角线一共有( )条
A.14B.21C.28D.42
8.若是方程的解,则( )
A.B.C.D.4
9.随着冬季的到来,某商场进行清场促销活动,将标价为120元的衬衫以八折降价出售仍可获利,设这件祄衫的成本为元,根据题意,可列方程( )
A.B.
C.D.
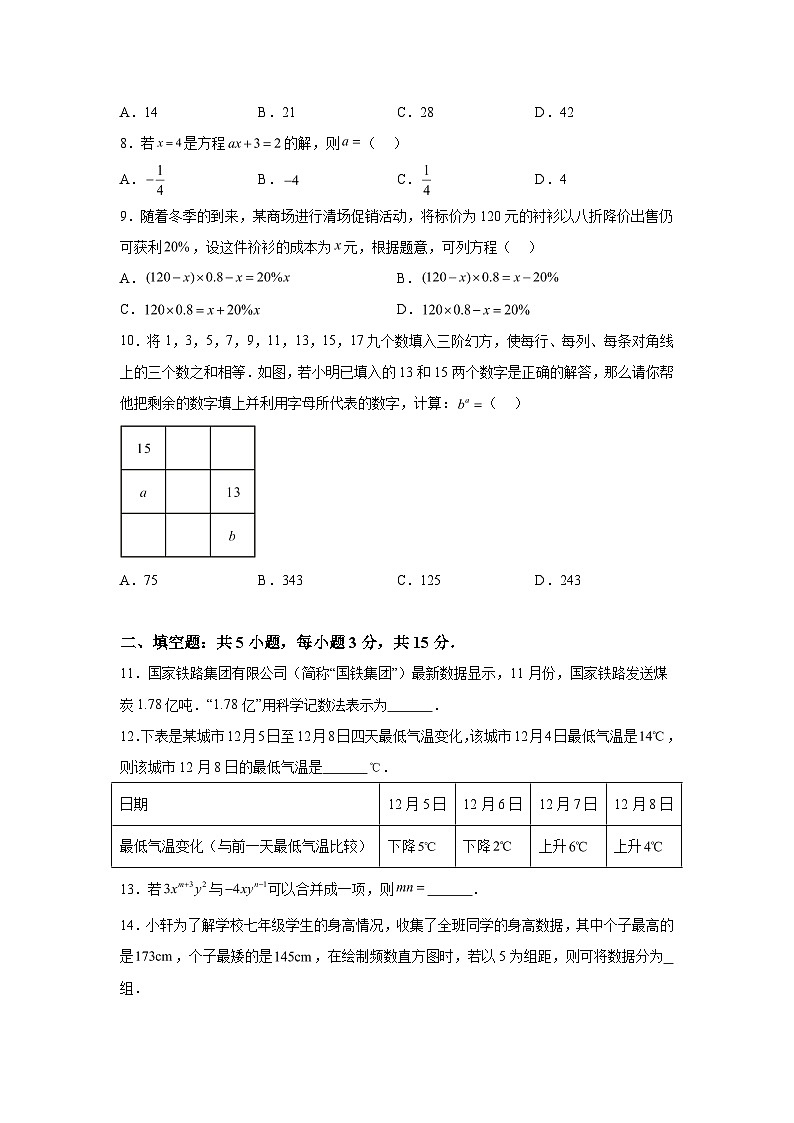
10.将1,3,5,7,9,11,13,15,17九个数填入三阶幻方,使每行、每列、每条对角线上的三个数之和相等.如图,若小明已填入的13和15两个数字是正确的解答,那么请你帮他把剩余的数字填上并利用字母所代表的数字,计算:( )
A.75B.343C.125D.243
二、填空题:共5小题,每小题3分,共15分.
11.国家铁路集团有限公司(简称“国铁集团”)最新数据显示,11月份,国家铁路发送煤炭1.78亿吨.“1.78亿”用科学记数法表示为 .
12.下表是某城市12月5日至12月8日四天最低气温变化,该城市12月4日最低气温是,则该城市12月8日的最低气温是 .
13.若与可以合并成一项,则 .
14.小轩为了解学校七年级学生的身高情况,收集了全班同学的身高数据,其中个子最高的是,个子最矮的是,在绘制频数直方图时,若以5为组距,则可将数据分为 组.
15.木材加工厂将一批木料按如图所示的规律依次摆放,第1堆放6根,第2堆放10根,第3堆放15根……则第10堆放有木料 根.
三、解答题一:共3小题,第16题10分,第17、18题各7分,共24分.
16.计算:
(1);
(2).
17.解方程:.
18.一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图1所示,其中小正方形中的数字表示在该位置的小立方块的个数.请在如图2和如图3的网格中分别画出从正面、左面看到的这个几何体的形状图.
四、解答题二:共3小题,每题9分,共27分.
19.已知多项式,其中,满足.
(1)若,,将多项式化简并求值;
(2)若多项式的值与字母的取值无关,求,的值.
20.某中学七年级在开展课后服务时,调查了部分同学的兴趣爱好(每位同学只能选择其中的一项),并根据调查数据绘制了如图1、图2两幅不完整的统计图.
请根据以上提供的信息解答下列问题:
(1)本次调查的同学人数是 ;“书法”对应的扇形圆心角的度数为 ;
(2)请补全条形统计图;
(3)学校七年级共600人,由此估计其中喜爱足球的学生约有多少人?
21.某中学组织七年级师生开展研学活动,需租车前往.现有甲、乙两种客车可供选择,它们的载客量和租金如表格所示,校方根据信息初步制定以下两种方案:
方案一:单独租用甲型客车若干辆,刚好坐满;
方案二:单独租用乙型客车可以少租2辆,但会有30个座位空余.
(1)参加此次研学活动的师生共多少人?
(2)以上两种方案,哪一种更划算?
(3)若可以同时租用两种客车,是否存在一种更划算的方案?若存在,请写出你的方案.
五、解答题三:共2小题,每题12分,共24分.
22.三角形和三角形的顶点互相重合,,,,.
(1)如图1,当与重合,时, ;
(2)如图2,三角形固定不动,将三角形绕点旋转,使点落到的延长线上,当,且射线平分时,求的度数;
(3)三角形固定不动,将三角形绕点旋转,当且射线平分时,求.
23.【建立模型】
数轴上两点,所表示的数分别为,,.
(1)若,两点到原点的距离相等,,请画出数轴,并标出,两点的位置;
(2)请写出与之间的数量关系,当时,求的值;
【拓展延伸】
(3)如图,数轴上两点,所表示的数分别为,4,点,是数轴上两动点,点从点出发以每秒1个单位的速度向运动,同时点从点出发以每秒2个单位的速度向运动,当时,求此时点对应的数.
参考答案与解析
1.B
【分析】本题考查常见几何体的识别,根据所给图形可直接得出答案.
【详解】解:所给图形上部为圆锥,下部为圆柱,可以看作圆锥与圆柱的组合体,
故选B.
2.C
【分析】本题考查相反意义的量.属性相同、表示的意义相反的量,叫作相反意义的量.根据定义逐项判断即可.
【详解】解:A,买入20台电脑与卖出20台电脑,具有相反意义的量,不合题意;
B,水位上升与水位下降,具有相反意义的量,不合题意;
C,减少与增高,不具有相反意义的量,符合题意;
D,向东走和向西走,具有相反意义的量,不合题意;
故选C.
3.B
【分析】本题考查数轴,根据点P在数轴上的位置即可求解.
【详解】解:由数轴可知点表示的数在和之间,
,
四个选项中的数只有在和之间,
故选B.
4.B
【分析】本题考查正方体的表面展开图,正方体的表面展开图中,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】解:由正方体的展开图特点可得:
“特”与“麻”相对, “鸡”与“远”相对, “清”与“色”相对,
故选B.
5.D
【分析】根据单项式的次数即为单项式中所有字母的指数和,据此解答即可.
【详解】解:单项式的次数是,
故选:D.
【点睛】本题考查了单项式次数的定义,熟记相关定义是解本题的关键.
6.A
【分析】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
【详解】解:A. 动车质检员对零部件的检查采用全面调查,故该选项符合题意;
B. 调查某批次方便面的防腐剂含量采用抽样调查,故该选项不符合题意;
C. 查北江某河段的水污染情况采用抽样调查,故该选项不符合题意;
D. 调查某市初中学生一天的睡眠时长采用抽样调查,故该选项不符合题意;
故选:A.
7.A
【分析】本题考查多边形的对角线条数,根据n边形对角线条数计算即可.
【详解】解:七边形的对角线条数为:(条),
故选A.
8.A
【分析】本题考查了一元一次方程的解,解一元一次方程;关键是掌握方程的解即为能使方程左右两边相等的未知数的值.根据方程的解为,将代入方程即可求出的值.
【详解】解:依题意,将代入方程,
得:,
解得:.
故选:A
9.C
【分析】本题考查了由实际问题抽象出一元一次方程,根据题意找出题中存在的等量关系:售价成本价利润,列方程即可.
【详解】解:设这件祄衫的成本为元,根据题意,
可列方程:,
故选C.
10.D
【分析】本题考查三阶幻方,根据已知条件求出每行、每列、每条对角线上的三个数之和,再求出中心位置的数,进而列一元一次方程求出a和b,代入求值即可.
【详解】解:9个数的和为:
每行、每列、每条对角线上的三个数之和为:,
9个数的平均数为:,
根据三阶幻方特点可知,数字9位于中心位置,
由可知:,,
解得,,
因此,
故选:D.
11.
【分析】此题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中,为整数,表示时关键要正确确定的值以及的值.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正数;当原数的绝对值时,是负数.
【详解】解:将1.78亿用科学记数法表示为:.
故答案为:.
12.17
【分析】本题考查有理数加减混合运算的应用,下降记作“”,上升记作“”,列式计算即可.
【详解】解:,
该城市12月8日的最低气温是,
故答案为:17.
13.
【分析】本题考查同类项,根据同类项中相同字母的系数相同可得m和n的值,即可求解.
【详解】解:与可以合并成一项,
与是同类项,
,,
,,
,
故答案为: .
14.6
【分析】此题考查的是组数的确定方法,组数=极差÷组距.计算最大值与最小值的差,除以组距即可求得.
【详解】解:,
故答案为:6.
15.78
【分析】本题考查图形的变化规律,观察图形可得:第n个图形最底层有根木料,共有(根),据此可得答案.
【详解】解:由图可知:第一个图形有木料根,
第二个图形有木料(根),
第三个图形有木料(根),
……
以此类推,第n个图有木料(根),
因此第10堆放有木料(根),
故答案为:78.
16.(1)
(2)
【分析】本题考查有理数的加减混合运算,含乘方的有理数的混合运算:
(1)按从左到右的顺序进行加减运算即可;
(2)先计算乘方,去绝对值,再计算乘除,最后计算加减.
【详解】(1)解:
(2)解:
17.
【分析】本题主要考查了一元一次方程的解法,解本题的关键是熟练掌握一元一次方程的解题步骤:去分母、去括号、移项、合并同类项、系数化为1.
【详解】
去分母,得
去括号,得
移项,得
合并同类项,得
系数化为1,得
18.见解析
【分析】本题考查从不同方向观察几何体,由已知条件可知,从正面看到的形状图有3列,每列小正方数形数目分别为3,2,1,从左面看到的形状图有2列,每列小正方形数目分别为3,1.据此可画出图形.
【详解】解:从正面、左面看到的这个几何体的形状图如下.
19.(1),3
(2),
【分析】本题考查了整式的化简求值,掌握整式加减的法则是解题的关键.
(1)先去括号,然后合并同类项,最后代入数值进行计算即可;
(2)先去括号,然后合并同类项,最后根据题意得出关于a、b的方程,解方程即可得.
【详解】(1)解:原式
把,代入得:原式
∵,
∴原式
(2)解:由(1)得:原式,
∵,
∴
把代入得:原式
∵多项式的值与字母的取值无关,
∴,,
解得:,
20.(1)100,36
(2)见解析
(3)90人
【分析】本题考查条形统计图、扇形统计图、利用样本估计总体等:
(1)根据选择“古筝”人数及所占百分数可求调查的同学人数;选择“书法”人数除以调查的同学人数再乘以360度即为对应的扇形圆心角的度数;
(2)求出选择“武术”“篮球”“足球”的人数,再补全条形统计图;
(3)用调查对象中喜爱足球的人数所占比例乘以七年级学生总数即可.
【详解】(1)解:由题意知,本次调查的同学人数是:(人),
“书法”对应的扇形圆心角的度数为:,
故答案为:100,36;
(2)解:选择“武术”的人数为:(人),
选择“篮球”的人数为:(人),
选择“足球”的人数为:(人),
补全后的条形统计图如下:
(3)解:(人),
即估计其中喜爱足球的学生约有90人.
21.(1)420人
(2)方案二更划算
(3)租3辆甲型客车,7辆乙型客车
【分析】本题考查了一元一次方程的应用,二元一次方程的正整数解问题,解题关键是找到题目中的等量关系.
(1)设单独租用甲型客车时租用x辆,则单独租用乙型客车时租用辆,根据已知数量关系列一元一次方程,求出x后,即可求解;
(2)用租用数量乘以单价求出两种方案的租金,比较大小即可;
(3)设租a辆甲型客车,b辆乙型客车,刚好师生都有座位,则得,取正整数解,计算相应的费用,并与方案一、方案二的费用进行比较即可得出答案.
【详解】(1)解:设单独租用甲型客车时租用x辆,
由题意知:,
解得,,
(人),
即参加此次研学活动的师生共420人.
(2)解:结合(1)中结论可知,
方案一的租车费用为:(元),
方案二的租车费用为:(元),
,
方案二更划算;
(3)解:设租a辆甲型客车,b辆乙型客车,刚好师生都有座位,
则,
解得正整数解为,
此方案的租车费用为:(元),
,
租3辆甲型客车,7辆乙型客车更划算.
22.(1)
(2)
(3)或
【分析】(1)根据已知条件,结合角度之间的关系计算即可;
(2)连接,利用三角形的内角和定理得出,再由角平分线定理得出,再根据等腰三角形的性质得出,由平角为得出,最后再利用三角形的内角和定理求出即可;
(3)分两种情况,当点E在线段上面时,根据题意得,由,即可求得;当点E在线段下面时,可得,由即可求得.
【详解】(1)解:∵当与重合,,,
∴,
故答案为∶.
(2)连接,如下图:
∵,,
∴,
∴平分,
∴,
∵,,
∴,
∵点落到的延长线上,
∴,
∴;
(3)①当点E在线段上面时,如图,
∵平分,
∴,
∵,,
∴,
则;
②当点E在线段下面时,如图,
∵平分,
∴,
∵,,
∴,
则;
故为或.
【点睛】本题主要考查角平分线的性质、等腰三角形的性质三角形内角和定理和旋转所成角度,解题的关键是分类讨论思想的应用和应用角平分性质.
23.(1)见解析;(2)或;(3)点对应的数或;
【分析】本题考查数轴上的动点问题,一元一次方程的应用.掌握两点间的距离公式,正确的列出方程,是解题的关键.(1)根据条件即可求出,,从而在数轴上表示;(2)根据题意得到即可求解;(3)表示出P,Q表示的数,根据,列出方程进行求解即可.
【详解】解:(1)∵,,两点到原点的距离相等,,
数轴上表示如下所示:
解:(2)∵数轴上两点,所表示的数分别为,,,,
∴,解得:或
解:(3)设运动时间为t,
由题意得:点对应的数:,点对应的数:,
∵,
∴,解得:或
∴或
∴点对应的数或;
日期
12月5日
12月6日
12月7日
12月8日
最低气温变化(与前一天最低气温比较)
下降
下降
上升
上升
甲型客车
乙型客车
载客量(人/辆)
35
45
租金(元/辆)
1100
1300
相关试卷
这是一份2023-2024学年广东省清远市英德市八年级上学期期中数学质量检测模拟试题(含解析),共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份广东省清远市英德市2023-2024学年七年级上学期期中数学试题,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份广东省清远市英德市2023-2024学年九年级上学期期中数学试题,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









