2023-2024学年广东省河源市连平县八年级（上）学期期末数学试题（含解析）

这是一份2023-2024学年广东省河源市连平县八年级（上）学期期末数学试题（含解析），共21页。试卷主要包含了选择题，填空题，解答题，解答题三等内容，欢迎下载使用。
一、选择题：共10小题，每小题3分，共30分．
1．已知直角三角形的两条直角边的长分别为5和12，则斜边长为（ ）
A．17B．16C．15D．13
2．点在正比例函数（）的图象上，则的值为（ ）
A．-15B．15C．D．
3．一块圆形蛋糕的直径长为，估计的值在（ ）
A．2与3之间B．3与4之间C．4与5之间D．5与6之间
4．如图是战机在空中展示的轴对称队形．以飞机所在直线为轴、队形的对称轴为轴，建立平面直角坐标系．若飞机的坐标为，则飞机的坐标为（ ）

A．B．C．D．
5．如图，矩形的边在数轴上，点A表示数0，点表示数4，．以点A为圆心，长为半径作弧，与数轴正半轴交于点，则点表示的数为（ ）

A．B．C．D．
6．下列运算一定正确的是（ ）
A．B．C．D．
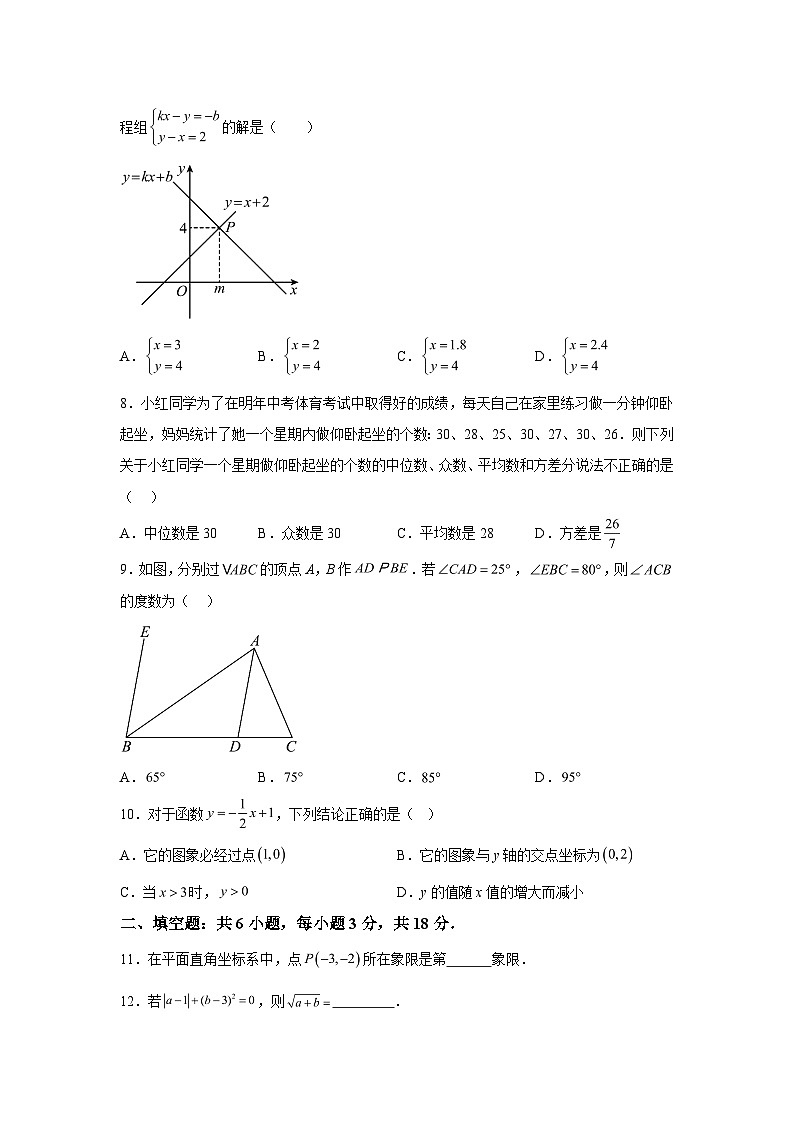
7．如图，一次函数与的图象相交于点，则关于x，y的二元一次方程组的解是（ ）

A．B．C．D．
8．小红同学为了在明年中考体育考试中取得好的成绩，每天自己在家里练习做一分钟仰卧起坐，妈妈统计了她一个星期内做仰卧起坐的个数：30、28、25、30、27、30、26．则下列关于小红同学一个星期做仰卧起坐的个数的中位数、众数、平均数和方差分说法不正确的是（ ）
A．中位数是30B．众数是30C．平均数是28D．方差是
9．如图，分别过的顶点A，B作．若，，则的度数为（ ）
A．B．C．D．
10．对于函数，下列结论正确的是（ ）
A．它的图象必经过点B．它的图象与y轴的交点坐标为
C．当时，D．y的值随x值的增大而减小
二、填空题：共6小题，每小题3分，共18分．
11．在平面直角坐标系中，点所在象限是第 象限．
12．若，则 ．
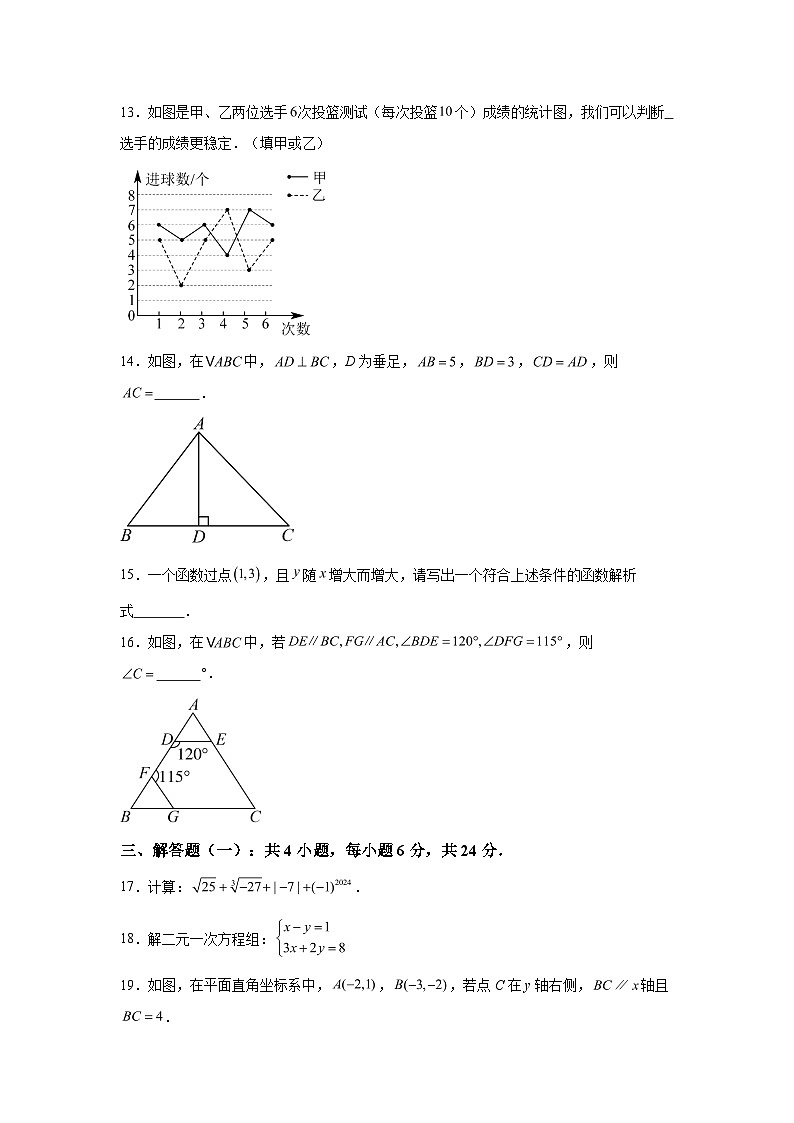
13．如图是甲、乙两位选手次投篮测试（每次投篮个）成绩的统计图，我们可以判断 选手的成绩更稳定．（填甲或乙）

14．如图，在中，，D为垂足，，，，则 ．

15．一个函数过点，且随增大而增大，请写出一个符合上述条件的函数解析式 ．
16．如图，在中，若，则 °．

三、解答题（一）：共4小题，每小题6分，共24分．
17．计算：．
18．解二元一次方程组：
19．如图，在平面直角坐标系中，，，若点C在y轴右侧，轴且．

(1)求点C的坐标；
(2)在图中画出，并求的面积：
(3)若点P在x轴上运动，连接AP，当线段AP长度最小时，点P的坐标为_____依据是_______．
20．如图，，，，垂足分别为，．

(1)求证：；
(2)若，，求的长．
四、解答题（二）：共3小题，每小题8分，共24分．
21．已知：如图，点D、E、F、G都在的边上，，，

(1)求证：；
(2)若平分，，求的度数．
22．某校八年级（1）班学生以跨学科主题学习为载体，综合运用体育、数学、生物学等知识，研究体育课的运动负荷．在体育课基本部分运动后，测量统计了部分学生的心率情况，按心率次数（次/分钟），分为如下五组：A组：，组：，组：，组：，组：．
其中A组数据为：73，65，74，68，74，70，66，56．
根据统计数据绘制了不完整的统计图（如图所示），请结合统计图解答下列问题：
(1)组数据的中位数是______次，众数是______次；
(2)组频数是_____，在统计图中组所对应的扇形圆心角是______度：
(3)一般运动的适宜心率为（次/分钟），该校共有2200名学生，依据此次跨学科研究结果，估计该校大约有多少名学生达到适宜心率．
23．根据气象研究，在最接近地球表面的对流层内，从海平面向上每升高，气温降低，而在对流层之上的平流层下层（又称同温层）内，气温基本保持不变．已知海平面气温为，设海拔处气温为．
(1)当时，请直接写出在对流层内与之间的函数关系式______；
(2)已知我国南海海域对流层高度为，我空军某部飞行员驾驶J-20战斗机在南海海域巡逻，根据仪表显示，机舱外温度为时，战机巡航海拔高度为，求此时该战机下方海面气温；
(3)在（2）的条件下，若战机继续攀升至海拔处（处于平流层下层），求此时机舱外温度．
五、解答题三：共2小题，每小题12分，共24分．
24．问题情境：如图①，一只蚂蚁在一个长为，宽为的长方形地毯上爬行，地毯上堆放着一根正三棱柱的木块，它的侧棱平行且等于宽，木块从正面看是一个边长为的等边三角形，求一只蚂蚁从点A处到达点C处需要走的最短路程．
(1)数学抽象：将蚂蚁爬行过的木块的侧面“拉直”“铺平”，“化曲为直”，请在图②中用虚线补全木块的侧面展开图，并用实线连接；
(2)线段的长即蚂蚁从点A处到达点C处需要走的最短路程，依据是_________；
(3)问题解决：求出这只蚂蚁从点A处到达点C处需要走的最短路程．
25．如下图，已知直线：与直线：交于点，两直线与x轴分别交于点B和点C．
(1)求直线和的函数表达式；
(2)求四边形的面积；
(3)如下图，点P为线段上一动点，将沿直线翻折得到，线段交x轴于点E．当为直角三角形时，请直接写出点P的坐标．
参考答案与解析
1．D
【分析】本题主要考查了勾股定理．根据勾股定理即可求解．
【详解】解：根据勾股定理得：
斜边长为．
故选：D
2．D
【分析】直接把已知点代入，即可求出k的值．
【详解】解：∵点在正比例函数的图象上，
∴，
∴，
故选：D．
【点睛】此题考查了用待定系数法求正比例函数的解析式，解题关键是正确得出k的值．
3．B
【分析】根据即可做出判断．
【详解】∵，即，
∴的值在3和4之间．
故选：B
【点睛】本题考查估算无理数的大小，正确估算出的范围是解题的关键．
4．A
【分析】根据轴对称的性质即可得到结论．
【详解】解：飞机与飞机关于轴对称，
飞机的坐标为，
故选：A．
【点睛】本题考查了坐标与图形变化对称，熟练掌握轴对称的性质是解题的关键．
5．C
【分析】根据勾股定理计算出的长度，进而求得该点与点A的距离，再根据点A表示的数，可得该点表示的数．
【详解】解：由题意得：，
∵，四边形是矩形，
∴，
∴，
∴，
∴点表示的数为，
故选：C．
【点睛】此题主要考查了勾股定理的应用，解决本题的关键是掌握勾股定理：在任何一个直角三角形中，两条直角边长的平方和一定等于斜边长的平方．
6．B
【分析】根据平方根、立方根的定义判断即可．
【详解】解：、，此选项错误，不符合题意；
、，此选项正确，符合题意；
、，此选项错误，不符合题意；
、，此选项错误，不符合题意；
故选：．
【点睛】本题考查算术平方根、立方根的定义，解题的关键是熟练掌握基本概念，属于中考基础题．
7．B
【分析】一次函数的交点坐标即为对应二元一次方程组的解．
【详解】解：将点代入得：
∴交点坐标为：
由一次函数与二元一次方程组的关系可得：该方程组的解为
故选：B
【点睛】本题考查一次函数与二元一次方程组的关系．掌握相关结论即可．
8．A
【分析】根据平均数的定义：一组数据的总和除以这组数据的个数所得的商，叫做这组数据的算术平均数，简称平均数；众数的定义：一组数据中出现次数最多的数据；中位数的定义：一组数据中，处在最中间或处在最中间的两个数的平均数；方差的定义：一组数据中各个数据与它们平均数的差的平方的和的平均数，进行求解即可．
【详解】解：把这组数据从小到大排列为：25、26、27、28、30、30、30，处在最中间的数是28，
∴中位数为28，故A选项正确，符合题意；
∵30出现的次数最多，
∴众数是30，故B选项不符合题意；
由题意得它们的平均数为：
，故选项C不符合题意；
方差：，故D选项不符合题意；
故选A．
【点睛】本题主要考查了平均数，中位数，众数和方差，解题的关键在于能够熟知相关定义．
9．B
【分析】根据两直线平行，同位角相等，得到，利用三角形内角和定理计算即可．
【详解】∵，，
∴，
∵，
∴，
故选B．
【点睛】本题考查了平行线的性质，三角形内角和定理，熟练掌握平行线性质是解题的关键．
10．D
【分析】根据函数解析式可知“它的图象必经过点”错误；根据函数解析式可知函数经过第一、二、四象限；根据一次函数的性质即可解答．
【详解】解：函数解析式为，
当时，，
“它的图象必经过点”错误，
故A项不符合题意；
函数解析式为，
函数与轴交于，与轴交于，
函数经过第一、二、四象限，
故B项不符合题意；
当时，，
当时，，
故C项不符合题意；
函数解析式为，
，
的值随值的增大而减小，
故D项符合题意；
故选：D．
【点睛】本题考查了一次函数的图象及性质，掌握一次函数的性质是解题的关键．
11．三
【分析】根据各象限内点的坐标特征解答．
【详解】解：的横坐标为负数，纵坐标为负数，
在第三象限，
故答案为：三．
【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解题的关键，四个象限的符号特点分别是：第一象限，第二象限，第三象限，第四象限．
12．
【分析】根据绝对值的非负性，平方的非负性求得的值进而求得的算术平方根即可求解．
【详解】解：∵，
∴，
解得：，
∴，
故答案为：．
【点睛】本题考查了求一个数的算术平方根，熟练掌握绝对值的非负性，平方的非负性求得的值是解题的关键．
13．甲
【分析】根据数据偏离平均数越大，即波动越大，数据越不稳定，方差越大；数据偏离平均数越小，即波动越小，数据越稳定，方差越小进行判断．
【详解】解：由图象可知：
甲选手次投篮次数为：6，5，6，4，7，6；
，
，
乙选手次投篮次数为：5，2，5，7，3，5，
，
，
，
故乙波动大，成绩不稳定，甲波动小，成绩更稳定．
故答案为：甲．
【点睛】本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
14．
【分析】先根据勾股定理求出的长度，再根据勾股定理求出即可．
【详解】解：∵，，，
∴，
∴，
∴，
故答案为：．
【点睛】本题主要考查了勾股定理，解题的关键是掌握直角三角形两直角边的平方和等于斜边的平方．
15．（答案不唯一）
【分析】根据题意及函数的性质可进行求解．
【详解】解：由一个函数过点，且随增大而增大，可知该函数可以为（答案不唯一）；
故答案为（答案不唯一）．
【点睛】本题主要考查正比例函数的性质，熟练掌握正比例函数的性质是解题的关键．
16．##55度
【分析】先由邻补角求得，，进而由平行线的性质求得，，最后利用三角形的内角和定理即可得解．
【详解】解：∵，，，
∴，，
∵，
∴，，
∵，
∴，
故答案为：．
【点睛】本题主要考查了邻补角，平行线的性质以及三角形的内角和定理，熟练掌握平行线的性质是解题的关键．
17．10
【分析】本题主要考查实数的混合运算、立方根及算术平方根，熟练掌握各个运算是解题的关键；因此此题可根据立方根、算术平方根进行求解．
【详解】解：
．
18．
【分析】采用加减消元法即可求解．
【详解】解：①，得②，
将②+③，得，
解得．
将代入①，
得，
∴方程组的解为：．
【点睛】本题主要考查了运用加减消元法解二元一次方程组的知识，掌握加减消元法是解答本题的关键．
19．(1)
(2)见解析，的面积6
(3)见详解
【分析】（1）因为轴，点C与点纵坐标相等，点C在y轴右侧，且，即可求出横坐标；
（2）利用三角形面积求解即可；
（3）利用“垂线段最短”，解答即可．
【详解】（1）解：轴，，点C在y轴右侧，且．
∴点C的坐标为：；
故答案为：；
（2）如图：

的面积：
（3）
当线段AP长度最小时，点P的坐标为，依据是直线外一点与直线上各点连线中垂线段最短．
【点睛】本题考查了作图-复杂作图，坐标与图形性质，解答本题的关键是准确作图．
20．(1)见解析
(2)
【分析】（1）利用“”可证明；
（2）先利用全等三角形的性质得到，再利用勾股定理计算出，从而得到的长，然后计算即可．
【详解】（1）证明：，，
，
在和中，
，
；
（2）解：，
，
在中，，
，
．
【点睛】本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
21．(1)见解析
(2)
【分析】（1）根据平行线的性质得到，继而推出，即可证明；
（2）利用平行线的性质得到，结合角平分线的定义求出，再利用平行线的性质求解即可．
【详解】（1）证明：，
，
，
，
；
（2）解：，
，
平分，
，
，
，
．
【点睛】此题考查平行线的性质，角平分线的定义，关键是根据平行线的判定和性质解答．
22．(1)69；74
(2)30；54
(3)大约有1650名学生达到适宜心率
【分析】本题主要考查中位数、众数、扇形与条形统计图，解题的关键是理清题中所给数据；
（1）根据题意及中位数、众数可进行求解；
（2）由统计图及扇形圆心角可进行求解；
（3）根据题意可直接进行求解．
【详解】（1）解：将A组数据从小到大排列为：56，65，66，68，70，73，74，74，
中位数为；
出现的次数最多，
众数是74；
故答案为69，74；
（2）解：由统计图可知：，
∴，
在统计图中组所对应的扇形圆心角是；
，
组的人数为30，
故答案为30；54；
（3）解：由题意得：（人），
答：大约有1650名学生达到适宜心率．
23．(1)
(2)此时该战机下方海面气温为
(3)战机继续攀升至海拔处，此时机舱外温度为
【分析】本题考查了利用一次函数解决实际问题．
（1）根据从海平面向上每升高，气温降低，即可列出与之间的函数关系式；
（2）由题意得关于之间的关系式为，且时，代入即可求出m的值为20，即此时该战机下方海面气温为；
（3）由（2）得关于之间的关系式为，求出时y的值，由于对流层之上的平流层下层（又称同温层）内，气温基本保持不变，，因此战机继续攀升至海拔处的温度与时的温度相同．
【详解】（1）依题意，从海平面向上每升高，气温降低，
当时，关于之间的关系式为；
故答案为：；
（2）根据题意得：战机巡航海拔高度为，即，，
关于之间的关系式为；
，
海面气温为；
（3）由（2）得关于之间的关系式为，
当时，，
对流层之上的平流层下层（又称同温层）内，气温基本保持不变，
战机继续攀升至海拔处，此时机舱外温度为．
24．(1)图形见解析
(2)两点之间线段最短.
(3)这只蚂蚁从点A处到达点C处需要走的最短路程为．
【分析】本题考查平面展开—最短路径问题，两点之间线段最短，勾股定理，要注意培养空间想象能力，解题的关键是熟练掌握两点之间线段最短．
（1）根据题意画出三棱柱木块的平面展开图，根据两点之间线段最短连接即可；
（2）根据题（1）结合两点之间线段最短即可求解；
（3）根据题意可得，展开图中等于长方形地毛毯的长和三角形一条边长之和，展开图中等于长方形地毛毯的宽，根据勾股定理计算的长即可求解．
【详解】（1）解：如图所示，即为所求：
（2）解：线段的长即蚂蚁从点处到达点处需要走的最短路程，依据是两点之间线段最短，
故答案为：两点之间线段最短；
（3）根据题意可得：展开图中的，．
在中，由勾股定理可得：，
即这只蚂蚁从点A处到达点C处需要走的最短路程为．
25．(1)直线的表达式为：，直线的表达式为：
(2)
(3)P点坐标为：或
【分析】（1）由待定系数法即可求解；
（2）由四边形的面积，即可求解；
（3）①当时，证明，得到，即可求解；②当时，得到，由勾股定理可求解．
【详解】（1）解：将点A的坐标分别代入两个函数表达式得：，
解得：，
则直线的表达式为：，则点，
直线的表达式为：，则点；
（2）解：由（1）知，，
，
点F在直线：上，则令，，
，则，
四边形的面积
；
（3）解：为直角三角形，分两种情况讨论：
①当时，
如图2，由对折可得，，
，
过点A作于G，
，
，
，
；
②当时，如图3所示：
由图可知：，
，
由对折得，，
，
设，则，
由勾股定理可知：，
则，
解得：，
∴，
，
∵P在x轴负半轴，
．
综上所述：P点坐标为：或．
【点睛】本题是一次函数综合题，考查了待定系数法，角平分线的性质，直角三角形的性质和判定，翻折的性质等，构造出图形是解本题的关键．