浙江省丽水市名校2023-2024学年九年级数学第一学期期末联考模拟试题含答案

这是一份浙江省丽水市名校2023-2024学年九年级数学第一学期期末联考模拟试题含答案，共8页。试卷主要包含了考生要认真填写考场号和座位序号，关于抛物线y＝－3，在中，，，下列结论中，正确的是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。
一、选择题（每题4分，共48分）
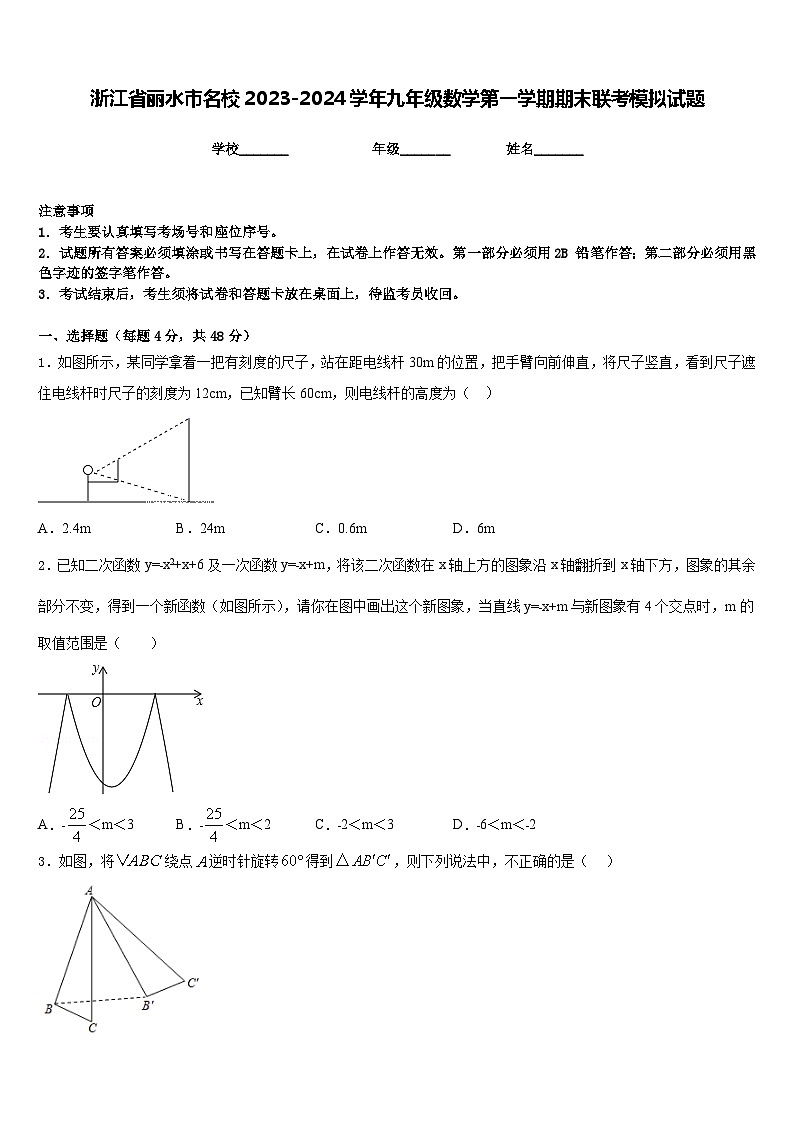
1．如图所示，某同学拿着一把有刻度的尺子，站在距电线杆30m的位置，把手臂向前伸直，将尺子竖直，看到尺子遮住电线杆时尺子的刻度为12cm，已知臂长60cm，则电线杆的高度为（ ）
A．2.4mB．24mC．0.6mD．6m
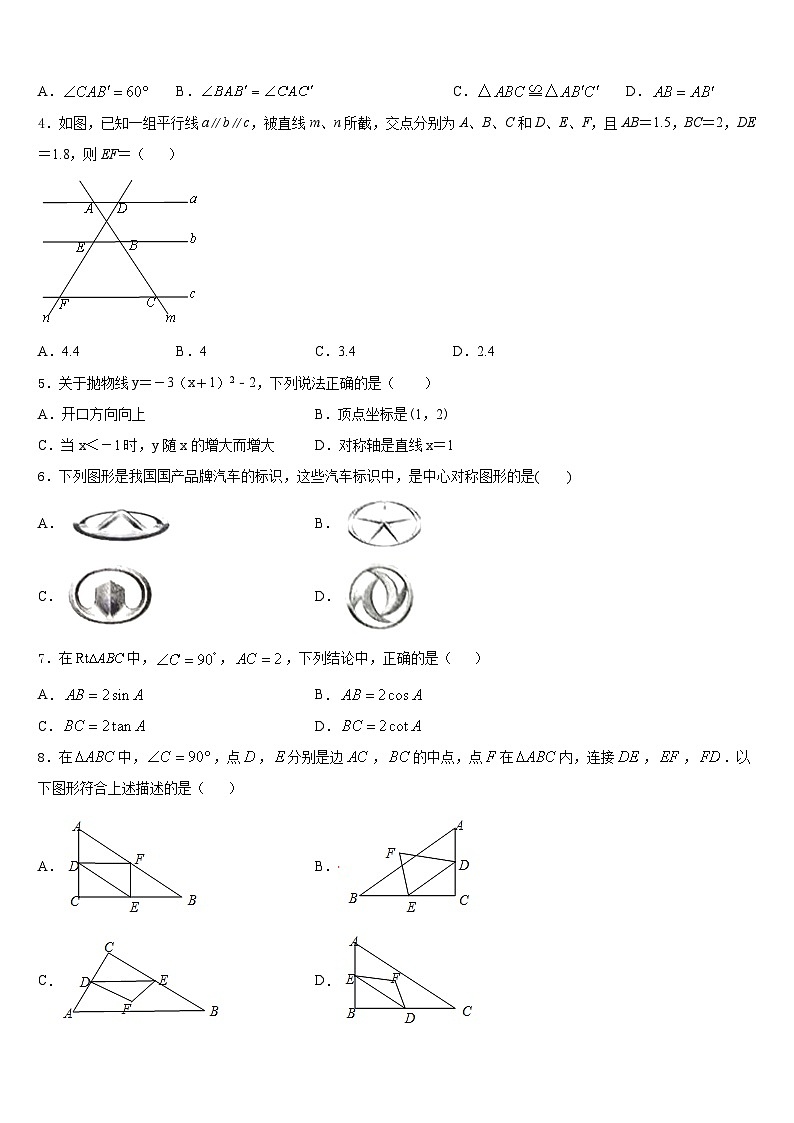
2．已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新函数（如图所示），请你在图中画出这个新图象，当直线y=﹣x+m与新图象有4个交点时，m的取值范围是（ ）
A．﹣＜m＜3B．﹣＜m＜2C．﹣2＜m＜3D．﹣6＜m＜﹣2
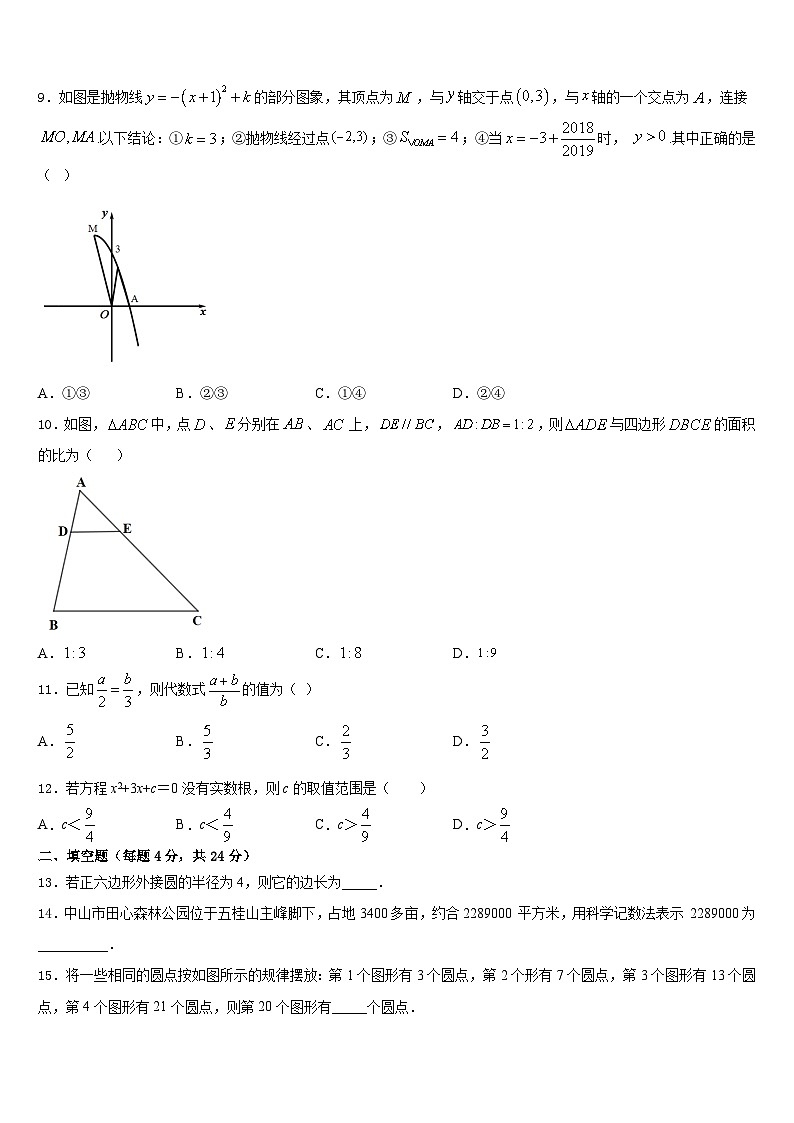
3．如图，将绕点逆时针旋转得到，则下列说法中，不正确的是（ ）
A．B．C．D．
4．如图，已知一组平行线a∥b∥c，被直线m、n所截，交点分别为A、B、C和D、E、F，且AB＝1.5，BC＝2，DE＝1.8，则EF＝（ ）
A．4.4B．4C．3.4D．2.4
5．关于抛物线y＝－3（x＋1）2﹣2，下列说法正确的是（ ）
A．开口方向向上B．顶点坐标是(1，2)
C．当x＜－1时，y随x的增大而增大D．对称轴是直线x＝1
6．下列图形是我国国产品牌汽车的标识，这些汽车标识中，是中心对称图形的是( )
A．B．
C．D．
7．在中，，，下列结论中，正确的是（ ）
A．B．
C．D．
8．在中，，点，分别是边，的中点，点在内，连接，，．以下图形符合上述描述的是（ ）
A．B．
C．D．
9．如图是抛物线的部分图象，其顶点为，与轴交于点，与轴的一个交点为，连接.以下结论：①；②抛物线经过点；③；④当时， .其中正确的是（ ）
A．①③B．②③C．①④D．②④
10．如图，中，点、分别在、上，，，则与四边形的面积的比为（ ）
A．B．C．D．
11．已知，则代数式的值为（ ）
A．B．C．D．
12．若方程x2+3x+c＝0没有实数根，则c的取值范围是（ ）
A．c＜B．c＜C．c＞D．c＞
二、填空题（每题4分，共24分）
13．若正六边形外接圆的半径为4，则它的边长为_____．
14．中山市田心森林公园位于五桂山主峰脚下，占地3400多亩，约合2289000 平方米，用科学记数法表示 2289000为__________．
15．将一些相同的圆点按如图所示的规律摆放：第1个图形有3个圆点，第2个形有7个圆点，第3个图形有13个圆点，第4个图形有21个圆点，则第20个图形有_____个圆点．
16．如图，在平面直角坐标系中，将绕点顺时针旋转到的位置，点，分别落在点，处，点在轴上，再将绕点顺时针旋转到的位置，点在轴上，再将绕点顺时针旋转到的位置，点在轴上，依次进行下去，……，若点，，则点B2016的坐标为______.
17．现有6张正面分别标有数字的不透明卡片，这些卡片除数字不同外其余全部相同现将它们背面朝上，洗均匀后从中任取一张，将该卡片上的数字记为，则使得关于的一元二次方程有实数根的概率为____．
18．如图，在平面直角坐标系中，已知点，为平面内的动点，且满足，为直线上的动点，则线段长的最小值为________.
三、解答题（共78分）
19．（8分）如图，，DB平分∠ADC，过点B作交AD于M．连接CM交DB于N．
（1）求证：；（2）若，求MN的长．
20．（8分）已知关于x的方程ax2+（3﹣2a）x+a﹣3＝1．
（1）求证：无论a为何实数，方程总有实数根．
（2）如果方程有两个实数根x1，x2，当|x1﹣x2|＝时，求出a的值．
21．（8分） “一带一路”为我们打开了交流、合作的大门，也为沿线各国在商贸等领域提供了更多的便捷，2018年11月5日至10日，首届中国国际进口博览会在国家会展中心（上海）举办，据哈外贸商会发布消息，博览会期间，哈Paseka公司与重庆某国际贸易公司签订了供应蜂蜜合同：哈Paseka公司于2019年6月前分期分批向重庆某国际贸易公司供给优质蜂蜜共3000万件，该公司顺应新时代购物流，打算分线上和线下两种方式销售．
（1）若计划线上销售量不低于线下销售量的25%，求该公司计划在线下销售量最多为多少万件？
（2）该公司在12月上旬销售优质蜂蜜共240万件，且线上线下销售单件均为100元/件．12月中旬决定线上销售单价下调m%，线下销售单价不变，在这种情况下，12月中旬销售总量比上旬增加了m%，且中旬线上销售量占中旬总销量的，结果中旬销售总金额比上旬销售总金额提高了m%．求m的值．
22．（10分）如图，等腰Rt△BPQ的顶点P在正方形ABCD的对角线AC上（P与AC不重合），∠PBQ=90°，QP与BC交于E,QP延长线交AD于F，连CQ.
(1)①求证：AP=CQ ；
②求证：
(2)当时，求的值.
23．（10分）解方程
（1）x2﹣4x+2＝0
（2）（x﹣3）2＝2x﹣6
24．（10分）如图，点A（1，m2）、点B（2，m﹣1）是函数y＝（其中x＞0）图象上的两点．
（1）求点A、点B的坐标及函数的解析式；
（2）连接OA、OB、AB，求△AOB的面积．
25．（12分）从三角形(不是等腰三角形)一个顶点引出一条射线 与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．
如图1，在中，是的完美分割线，且， 则的度数是
如图2，在中，为角平分线，，求证: 为的完美分割线．
如图2，中，是的完美分割线，且是以为底边的等腰三角形，求完美分割线的长．
26．（12分）某校一课外活动小组为了了解学生最喜欢的球类运动况,随机抽查了本校九年级的200名学生,调查的结果如图所示，请根据该扇形统计图解答以下问题：
(1)图中的值是________；
(2)被查的200名生中最喜欢球运动的学生有________人；
(3)若由3名最喜欢篮球运动的学生(记为),1名最喜欢乒乓球运动的学生(记为),1名最喜欢足球运动的学生(记为)组队外出参加一次联谊活动．欲从中选出2人担任组长(不分正副),列出所有可能情况,并求2人均是最喜欢篮球运动的学生的概率．
参考答案
一、选择题（每题4分，共48分）
1、D
2、D
3、A
4、D
5、C
6、D
7、C
8、C
9、D
10、C
11、B
12、D
二、填空题（每题4分，共24分）
13、1
14、
15、1
16、（6048，2）
17、
18、
三、解答题（共78分）
19、（1）见解析；（2）.
20、（1）见解析；（2）﹣2或2
21、（1）2400万件；（2）1
22、（1）①证明见解析；②证明见解析；（2）
23、（1）x＝2；（2）x＝3或x＝1．
24、（1）A（1，2），B（2，1），函数的解析式为y＝；（2）
25、（1）88°；（2）详见解析；（3）
26、（1）35；（2）190；（3）所有可能的情况见解析，．