浙江省金华市金东区2023-2024学年九上数学期末监测模拟试题含答案

这是一份浙江省金华市金东区2023-2024学年九上数学期末监测模拟试题含答案，共8页。试卷主要包含了化简的结果是，一元二次方程的解为等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题（每题4分，共48分）
1．在Rt△ABC中，∠C＝90°，AB＝10，sin∠B＝，则BC＝（ ）
A．15B．6C．9D．8
2．如图，是的直径，是的弦，若，则（ ）．
A．B．C．D．
3．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，那么下列说法正确的是（ ）
A．a＞0，b＞0，c＞0B．a＜0，b＞0，c＞0C．a＜0，b＞0，c＜0D．a＜0，b＜0，c＞0
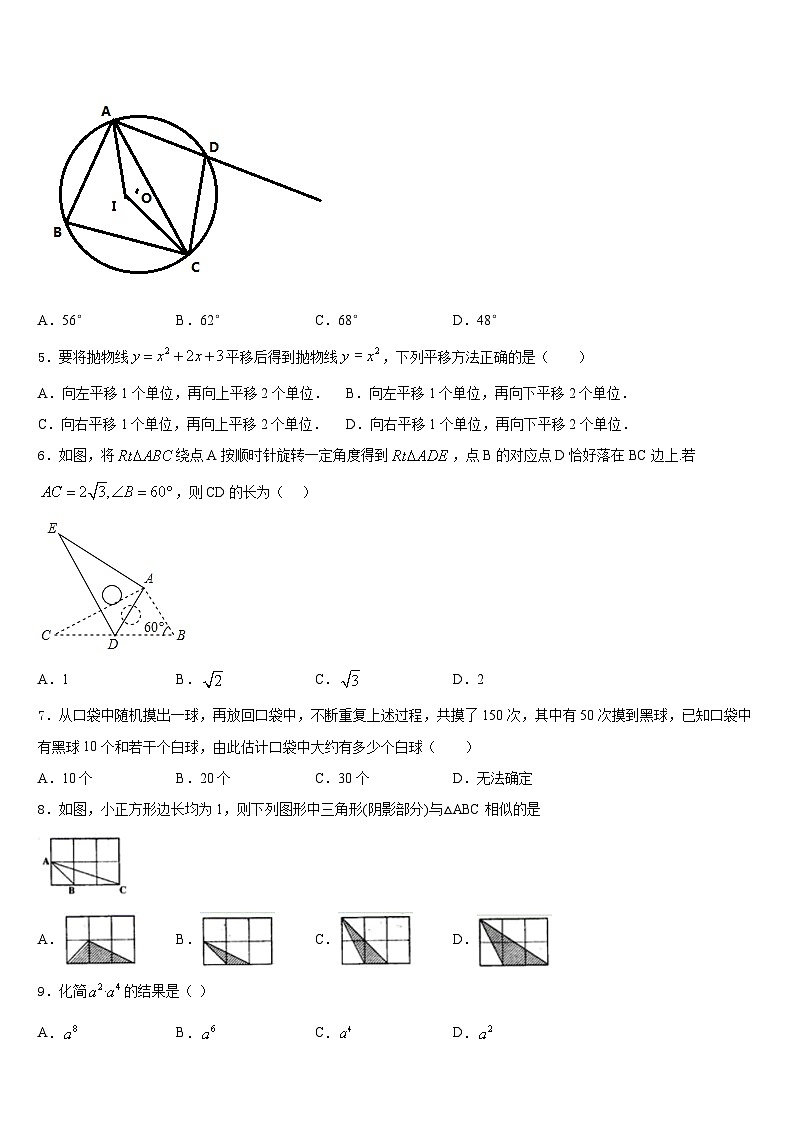
4．四边形内接于⊙，点是的内心，，点在的延长线上，则的度数为( )
A．56°B．62°C．68°D．48°
5．要将抛物线平移后得到抛物线，下列平移方法正确的是（ ）
A．向左平移1个单位，再向上平移2个单位．B．向左平移1个单位，再向下平移2个单位．
C．向右平移1个单位，再向上平移2个单位．D．向右平移1个单位，再向下平移2个单位．
6．如图，将绕点A按顺时针旋转一定角度得到，点B的对应点D恰好落在BC边上.若，则CD的长为（ ）
A．1B．C．D．2
7．从口袋中随机摸出一球，再放回口袋中，不断重复上述过程，共摸了150次，其中有50次摸到黑球，已知口袋中有黑球10个和若干个白球，由此估计口袋中大约有多少个白球（ ）
A．10个B．20个C．30个D．无法确定
8．如图，小正方形边长均为1，则下列图形中三角形(阴影部分)与△ABC相似的是
A．B．C．D．
9．化简的结果是（ ）
A．B．C．D．
10．一元二次方程的解为（ ）
A．B． ，C． ，D．，
11．估计 ，的值应在( )
A．1和2之间B．2和3之间C．3和4之间D．4和5之间
12．下列命题正确的是( )
A．对角线相等四边形是矩形
B．相似三角形的面积比等于相似比
C．在反比例函数图像上，随的增大而增大
D．若一个斜坡的坡度为，则该斜坡的坡角为
二、填空题（每题4分，共24分）
13．如图，AC是⊙O的直径，弦BD⊥AC于点E，连接BC过点O作OF⊥BC于点F，若BD＝12cm，AE＝4cm，则OF的长度是___cm．
14．将抛物线向上平移3个单位长度，再向右平移2个单位长度，所得到的抛物线解析式为______．
15．如图，在□ABCD中，E、F分别是AD、CD的中点，EF与BD相交于点M，若△DEM的面积为1，则□ABCD的面积为________．
16．对于任意非零实数a、b，定义运算“”，使下列式子成立：，，，，…，则ab= ．
17．数据8，8，10，6，7的众数是__________．
18．如图，为矩形对角线，的交点，AB=6，M，N是直线BC上的动点，且，则的最小值是_．
三、解答题（共78分）
19．（8分）如图，△OAB中，OA＝OB＝10cm，∠AOB＝80°，以点O为圆心，半径为6cm的优弧分别交OA、OB于点M、N．
(1)点P在右半弧上(∠BOP是锐角)，将OP绕点O逆时针旋转80°得OP′．求证：AP＝BP′；
(2)点T在左半弧上，若AT与圆弧相切，求AT的长．
(3)Q为优弧上一点，当△AOQ面积最大时，请直接写出∠BOQ的度数为 ．
20．（8分）如图，已知是的直径，弦于点，是的外角的平分线．求证：是的切线．
21．（8分）如图，AB为⊙O的直径，C为⊙O上一点，D为的中点．过点D作直线AC的垂线，垂足为E，连接OD．
（1）求证：∠A=∠DOB；
（2）DE与⊙O有怎样的位置关系？请说明理由．
22．（10分）如图，在平面直角坐标系中，点是轴正半轴上的一动点，抛物线(是常数，且过点，与轴交于两点，点在点左侧，连接，以为边做等边三角形，点与点在直线两侧．
（1）求B、C的坐标；
（2）当轴时，求抛物线的函数表达式；
（3）①求动点所成的图像的函数表达式；
②连接，求的最小值．
23．（10分）已知一次函数的图象与轴和轴分别交于、两点，与反比例函数的图象分别交于、两点．
（1）如图，当，点在线段上（不与点、重合）时，过点作轴和轴的垂线，垂足为、．当矩形的面积为2时，求出点的位置；
（2）如图，当时，在轴上是否存在点，使得以、、为顶点的三角形与相似？若存在，求出点的坐标；若不存在，说明理由；
（3）若某个等腰三角形的一条边长为5，另两条边长恰好是两个函数图象的交点横坐标，求的值．
24．（10分）利川市南门大桥是上世纪90年代修建的一座石拱桥，其主桥孔的横截面是一条抛物线的一部分，2019年在维修时，施工队测得主桥孔最高点到水平线的高度为.宽度为.如图所示，现以点为原点，所在直线为轴建立平面直角坐标系.
（1）直接写出点及抛物线顶点的坐标；
（2）求出这条抛物线的函数解析式；
（3）施工队计划在主桥孔内搭建矩形“脚手架”，使点在抛物线上，点在水平线上，为了筹备材料，需求出“脚手架”三根钢管的长度之和的最大值是多少？请你帮施工队计算.
25．（12分）解方程：3x（1x+1）=4x+1．
26．（12分）某汽车销售商推出分期付款购车促销活动，交首付款后，余额要在30个月内结清，不计算利息，王先生在活动期间购买了价格为12万元的汽车，交了首付款后平均每月付款万元，个月结清．与的函数关系如图所示，根据图像回答下列问题：
（1）确定与的函数解析式，并求出首付款的数目；
（2）王先生若用20个月结清，平均每月应付多少万元？
（3）如果打算每月付款不超过4000元，王先生至少要几个月才能结清余额？
参考答案
一、选择题（每题4分，共48分）
1、D
2、B
3、B
4、C
5、D
6、D
7、B
8、B
9、B
10、C
11、B
12、D
二、填空题（每题4分，共24分）
13、.
14、
15、16
16、
17、1
18、2
三、解答题（共78分）
19、（1）证明见解析；（2）AT＝8；(3)170°或者10°．
20、见解析
21、（1）见解析；（2）相切，理由见解析
22、（1）、；（2）；（3）①；②．
23、（1）或；（2）存在，或；（3）
24、（1）；（2），；（3）三根钢管的长度之和的最大值是.
25、=,= −．
26、（1）y=，3万元；（2）0.45万元；（3）23个月才能结清余款