黑龙江省齐齐哈尔市龙沙区2023-2024学年九年级数学第一学期期末经典试题含答案

这是一份黑龙江省齐齐哈尔市龙沙区2023-2024学年九年级数学第一学期期末经典试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题（每题4分，共48分）
1．甲、乙、丙、丁四人各进行了次射击测试，他们的平均成绩相同，方差分别是则射击成绩最稳定的是（ ）
A．甲B．乙C．丙D．丁
2．已知函数y＝ax2+bx+c（a≠1）的图象如图，给出下列4个结论：①abc＞1； ②b2＞4ac； ③4a+2b+c＞1；④2a+b＝1．其中正确的有（ ）个．
A．1B．2C．3D．4
3．下列函数中，是反比例函数的是（ ）
A．B．C．D．
4．如图1，一个扇形纸片的圆心角为90°，半径为1．如图2，将这张扇形纸片折叠，使点A与点O恰好重合，折痕为CD，图中阴影为重合部分，则阴影部分的面积为( )
A．1π﹣B．1π﹣9C．12π﹣D．
5．在美术字中，有些汉字是中心对称图形，下面的汉字不是中心对称图形的是（ ）
A．B．C．D．
6．若x＝2是关于x的一元二次方程x2﹣2a＝0的一个根，则a的值为（ ）
A．3B．2C．4D．5
7．直线与抛物线只有一个交点，则的值为（ ）
A．B．C．D．
8．如图，在平面直角坐标系中，直线OA过点(4，2)，则的值是( )
A．B．C．D．2
9．某商场降价销售一批名牌衬衫,已知所获利润y(元)与降价x(元)之间的关系是y=-2x2+60x+800,则利润获得最多为( )
A．15元B．400元C．800元D．1250元
10．下列二次根式中，是最简二次根式的是（ ）
A．B．C．D．
11．如图，已知AB∥CD∥EF，它们依次交直线l1、l2于点A、D、F和点B、C、E，如果AD：DF＝3：1，BE＝10，那么CE等于( )
A．B．C．D．
12．已知的半径为，点的坐标为，点的坐标为，则点与的位置关系是（ ）
A．点在外B．点在上C．点在内D．不能确定
二、填空题（每题4分，共24分）
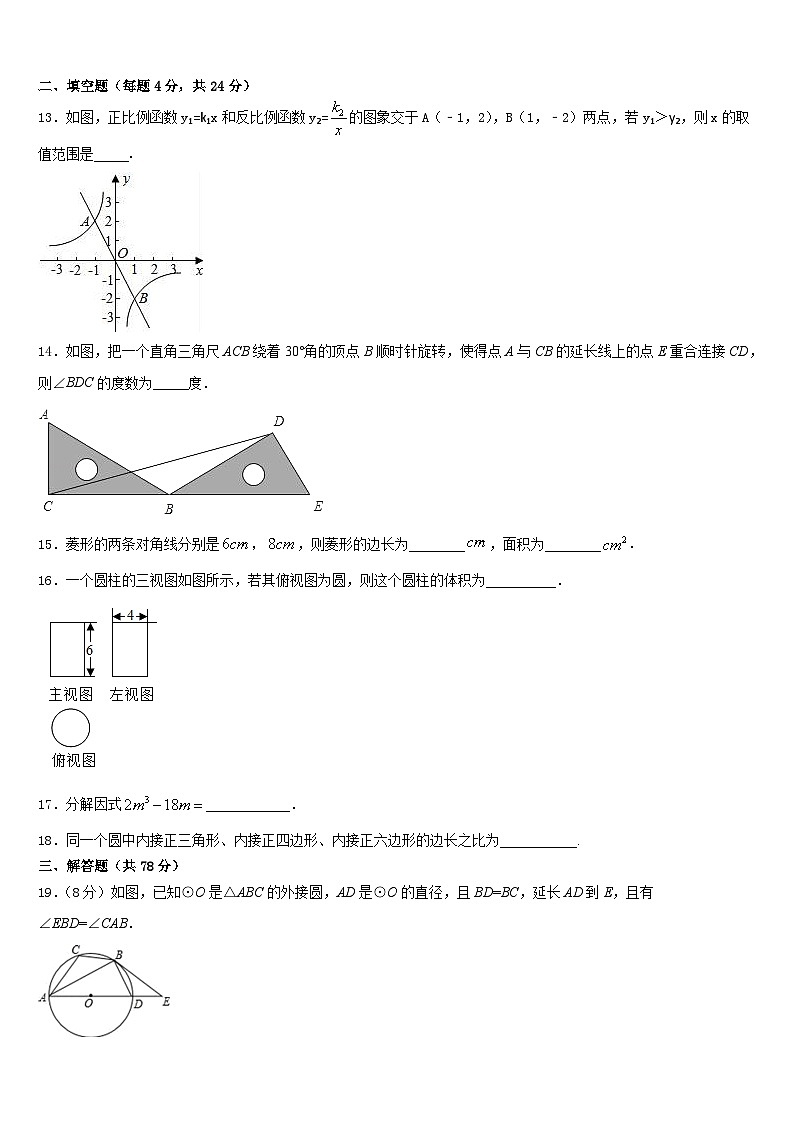
13．如图，正比例函数y1=k1x和反比例函数y2=的图象交于A（﹣1，2），B（1，﹣2）两点，若y1＞y2，则x的取值范围是_____．
14．如图，把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转，使得点A与CB的延长线上的点E重合连接CD，则∠BDC的度数为_____度．
15．菱形的两条对角线分别是，，则菱形的边长为________，面积为________．
16．一个圆柱的三视图如图所示，若其俯视图为圆，则这个圆柱的体积为__________．
17．分解因式____________．
18．同一个圆中内接正三角形、内接正四边形、内接正六边形的边长之比为___________.
三、解答题（共78分）
19．（8分）如图，已知⊙O是△ABC的外接圆，AD是⊙O的直径，且BD=BC，延长AD到E，且有∠EBD=∠CAB．
⑴求证：BE是⊙O的切线；
⑵若BC=，AC=5，求圆的直径AD的长．
20．（8分）如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转 270°后得到扇形COD,AP,BQ分别切优弧CD于点P，Q，且点P，Q在AB异侧，连接OP.
（1）求证：AP=BQ；
（2）当BQ= 时,求的长(结果保留 )；
（3）若△APO的外心在扇形COD的内部，求OC的取值范围.
21．（8分）指出“垃圾分类工作就是新时尚”．某小区为响应垃圾分类处理，改善生态环境，将生活垃圾分成三类：厨余垃圾、可回收垃圾和其他垃圾，分别记为a，b，c，并且设置了相应的垃圾箱：“厨余垃圾”箱、“可回收垃圾”箱和“其他垃圾”箱，分别记为A，B，C．
（1）若小明将一袋分好类的生活垃圾随机投入一类垃圾箱，画树状图求垃圾投放正确的概率；
（2）为了了解居民生活垃圾分类投放的情况，现随机抽取了小区某天三类垃圾箱中总共10吨的生活垃圾，数据统计如下（单位：吨）：
该小区所在的城市每天大约产生500吨生活垃圾，根据以上信息，试估算该城市生活垃圾中的“厨余垃圾”每月（按30天）有多少吨没有按要求投放．
22．（10分）如图①，四边形ABCD与四边形CEFG都是矩形，点E，G分别在边CD，CB上，点F在AC上，AB＝3，BC＝4
（1）求的值；
（2）把矩形CEFG绕点C顺时针旋转到图②的位置，P为AF，BG的交点，连接CP
（Ⅰ）求的值；
（Ⅱ）判断CP与AF的位置关系，并说明理由．
23．（10分）如图，以AB边为直径的⊙O经过点P，C是⊙O上一点，连结PC交AB于点E，且∠ACP=60°，PA=PD．
（1）试判断PD与⊙O的位置关系，并说明理由；
（2）若点C是弧AB的中点，已知AB=4，求CE•CP的值．
24．（10分）已知关于x的方程x2-（m+3）x+m+1＝1．
（1）求证：不论m为何值，方程都有两个不相等的实数根；
（2）若方程一根为4，以此时方程两根为等腰三角形两边长，求此三角形的周长．
25．（12分）某校园艺社计划利用已有的一堵长为10m的墙，用篱笆围一个面积为的矩形园子.
(1)如图，设矩形园子的相邻两边长分别为、.
①求y关于x的函数表达式；
②当时，求x的取值范围；
(2)小凯说篱笆的长可以为9.5m，洋洋说篱笆的长可以为10.5m.你认为他们俩的说法对吗？为什么？
26．（12分）在一个不透明的盒子里装有黑、白两种颜色的球共50个，这些球除颜色外其余完全相同．王颖做摸球试验，搅匀后，她从盒子里随机摸出一个球记下颜色后，再把球放回盒子中，不断重复上述过程，如表是试验中的一组统计数据：
（1）请估计：当n很大时，摸到白球的频率将会接近 ；（精确到0.1）
（2）若从盒子里随机摸出一个球，则摸到白球的概率的估计值为 ；
（3）试估算盒子里黑、白两种颜色的球各有多少个？
参考答案
一、选择题（每题4分，共48分）
1、C
2、C
3、B
4、A
5、A
6、A
7、D
8、A
9、D
10、B
11、C
12、B
二、填空题（每题4分，共24分）
13、x＜﹣2或0＜x＜2
14、1
15、
16、
17、
18、
三、解答题（共78分）
19、（1）详见解析；（2）1
20、（1）详见解析；（2）；（3）421、（1）垃圾投放正确的概率为；（2）该城市生活垃圾中的“厨余垃圾”每月（按30天）没有按要求投放的数量为3000（吨）．
22、（1）；（2）（Ⅰ）；（Ⅱ）CP⊥AF，理由：见解析.
23、（1）PD是⊙O的切线．证明见解析.（2）1.
24、（1）见解析；（2）
25、（1）①，②；（2）小凯的说法错误，洋洋的说法正确．
26、（1）0.6；（2）0.6；（3）盒子里黑颜色的球有20只，盒子白颜色的球有30只
A
B
C
a
3
0.8
1.2
b
0.26
2.44
0.3
c
0.32
0.28
1.4
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
65
124
178
302
480
600
1800
摸到白球的频率
0.65
0.62
0.593
0.604
0.6
0.6
0.6