2022-2023学年福建省厦门市同安区八年级下学期数学期末考模拟

这是一份2022-2023学年福建省厦门市同安区八年级下学期数学期末考模拟，文件包含福建省厦门市同安区八年级下学期数学期末考模拟docx、福建省厦门市同安区八年级下学期数学期末考模拟答案docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。
A．B．C．D．
【答案】D
2．（4分）同学某体育项目7次测试成绩如下（单位：分）：9，7，10，8，10，9，10．这组数据的众数为（ ）
A．10B．9C．8D．7
【答案】A
3．（4分）下列运算正确的是（ ）
A．B．C．D．
【答案】D
4．（4分）如图，四边形ABCD是平行四边形，点M在边AB上，AE⊥BC，MN⊥CD，垂足分别为E、N，则平行线AB与CD之间的距离是（ ）
A．AE的长B．MN的长C．AB的长D．AC的长
【答案】B
5．（4分）如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，则点C到直线AB的距离是（ ）
A．B．3C．D．2
【答案】C
6．（4分）在平面直角坐标系内，一次函数y＝ax+b的图象如图所示，那么下列说法正确的是（ ）
A．当x＞0时，﹣2＜y＜0
B．方程ax+b＝0的解是x＝﹣2
C．当y＞﹣2时，x＞0
D．不等式ax+b≤0的解集是x≤0
【答案】C
7．（4分）林则徐纪念馆作为“福州古雁”的典型代表，是全国重点文物保护单位．该纪念馆计划招聘一名工作人员，评委从内容、文化两个方面为甲、乙、丙、丁四位应聘者打分（具体分数如表），按内容占40%，文化占60%计算应聘者综合分，并录用综合分最高者，则最终录用的应聘者是（ ）
A．甲B．乙C．丙D．丁
【答案】D
8．（4分）如图，矩形ABCD中，∠AOB＝60°，AB＝3，则BD的长是（ ）
A．3B．5C．3D．6
【答案】D
9．（4分）如图是函数y＝f（x）的图象，根据图象提供的信息下列结论中错误的是（ ）
A．f（5）＝0
B．当3≤x≤7时，﹣2≤y≤4
C．f（6）＝﹣2
D．当3≤x≤6时，y随x的增大而增大
【答案】D
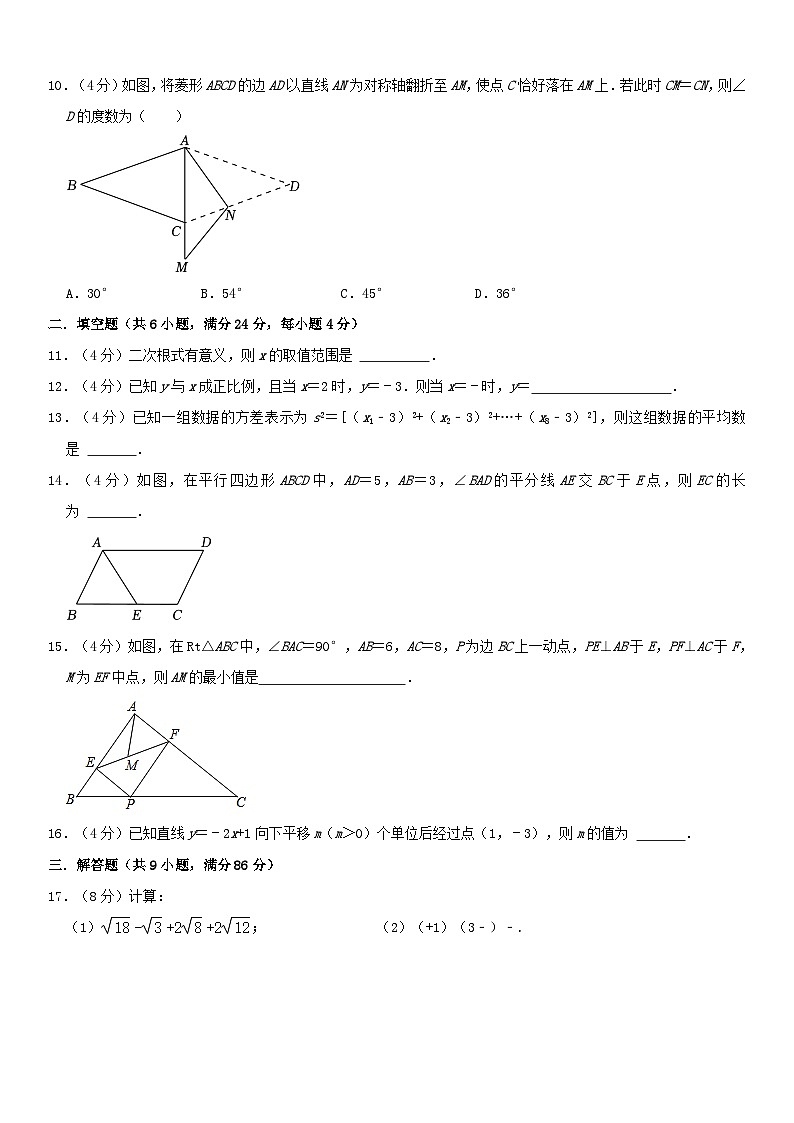
10．（4分）如图，将菱形ABCD的边AD以直线AN为对称轴翻折至AM，使点C恰好落在AM上．若此时CM＝CN，则∠D的度数为（ ）
A．30°B．54°C．45°D．36°
【答案】D
二．填空题（共6小题，满分24分，每小题4分）
11．（4分）二次根式有意义，则x的取值范围是 x≤3 ．
【答案】x≤3．
12．（4分）已知y与x成正比例，且当x＝2时，y＝﹣3．则当x＝﹣时，y＝ ．
【答案】．
13．（4分）已知一组数据的方差表示为s2＝[（x1﹣3）2+（x2﹣3）2+…+（x8﹣3）2]，则这组数据的平均数是 3 ．
【答案】3．
14．（4分）如图，在平行四边形ABCD中，AD＝5，AB＝3，∠BAD的平分线AE交BC于E点，则EC的长为 2 ．
【答案】2．
15．（4分）如图，在Rt△ABC中，∠BAC＝90°，AB＝6，AC＝8，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值是 ．
【答案】见试题解答内容
16．（4分）已知直线y＝﹣2x+1向下平移m（m＞0）个单位后经过点（1，﹣3），则m的值为 2 ．
【答案】2．
三．解答题（共9小题，满分86分）
17．（8分）计算：
（1）；
（2）（+1）（3﹣）﹣．
【答案】（1）7+3；
（2）﹣2．
18．（8分）如图，在平行四边形ABCD中，点E、F分别在边BC和AD上，且BE＝DF．
求证：四边形AECF是平行四边形．
【答案】证明见解析．
19．（8分）已知：一次函数y＝kx+b的图象经过M（0，2），N（1，3）两点，
（1）求一次函数的解析式，并画出此一次函数的图象；
（2）求当x取何值时，函数值y＞0．
【答案】（1）一次函数的解析式为y＝x+2，图象见解析图；
（2）当x＞﹣2时，y＞0．
20．（8分）先化简，再求值：，其中．
【答案】，﹣2．
21．（8分）如图，在△ABC中，D，E分别是边AB，AC的中点．
（1）求作：平行四边形ADCF（要求：尺规作图，保留作图痕迹，不写作法）；
（2）在（1）所作的图形中，若∠ACB＝90°，求证：平行四边形ADCF是菱形．
【答案】（1）作图见解析部分；
（2）证明见解析部分．
22．（10分）某校为了落实《中共中央国务院关于全面加强新时代大中小学劳动教育的意见》，培养学生的劳动意识，开展了系列宣讲活动．为了解本次宣讲活动效果，现从九年级随机抽取若干名学生，调查他们宣讲前后平均每周劳动时间情况，以下是根据调查结果绘制的统计图表：
宣讲前平均每周劳动时间频数统计表
请根据图表中的信息，解答下列问题：
（1）频数统计表中a＝ 5 ，宣讲前平均每周劳动时间的中位数落在 B 组；
（2）求宣讲后平均每周劳动时间的平均数（每组中各个数据用该组的中间值代替，如90～120的中间值为105）；
（3）教育部规定中学生每周劳动时间不低于3小时，若该校九年级共有600名学生，则宣讲后有多少名学生达到要求？
【答案】（1）5，B；
（2）宣讲后平均每周劳动时间的平均数是189min；
（3）宣讲后有384名学生达到要求．
23．（10分）已知四边形ABCD是菱形，A，B，C，D四点的坐标分别是（0，b），（m，m+1）（m＞0），（e，f），（m，m+3），直线y＝x+4经过点A，D，求直线CD的解析式．
【答案】见试题解答内容
24．（12分）“双减”政策颁布后，各校重视了延迟服务，并在延迟服务中加大了体育活动的力度．某体育用品商店抓住商机，计划购进300套乒乓球拍和羽毛球拍进行销售，其中购进乒乓球拍的套数不超过150套，它们的进价和售价如下表：
已知购进2套乒乓球拍和1套羽毛球拍需花费110元，购进4套乒乓球拍和3套羽毛球拍需花费260元．
（1）求出a，b的值；
（2）该面店根据以往销售经验，决定购进乒乓球拍套数不少于羽毛球拍套数的一半，设购进乒乓球拍x（套），售完这批体育用品获利y（元）．
①求y与x的函数关系式，并写出x的取值范围；
②该商店实际采购时，恰逢“双十一”购物节，乒乓球拍的进价每套降低了a元（0＜α∠10），羽毛球拍的进价不变，已知商店的售价不变，这批体育用品能够全部售完，则如何购货才能获利最大？
【答案】（1）a的值为35元，b的值为40元；
（2）①y与x的函数关系式为y＝﹣5x+6000，x的取值范围为：100≤x≤150；②当a＜5时，乒乓球拍购进10O套，羽毛球拍购进200套能获利最大；当a＝5时，当a＞5时，乒乓球和羽毛球任意选购利润一样大；乒乓球拍购进150套，羽毛球拍购进150套能获利最大．
25．（14分）综合与实践
问题情境：综合与实践课上，老师让同学们以“矩形纸片的折叠”为主题开展数学活动．矩形纸片ABCD中，AB＝4，．
操作探究：如图1，将矩形纸片ABCD沿过点A的直线折叠，使点D的对应点D'落在边BC上，展开后折痕AE交CD于点E．
（1）∠AD'B的度数为 45° ．
（2）求线段DE的长度．
拓展延伸：
（3）如图2，在图1的基础上，继续沿过点A的直线折叠，使点B的对应点落在AD'上，展开后折痕交BC于点F，连接EF．请判断△AEF的形状并说明理由．
【答案】（1）45°；
（2）；
（3）等腰直角三角形，证明见解析．应聘者
内容
文化
甲
80
85
乙
85
80
丙
90
80
丁
80
90
组别
频数
频率
A
30≤t＜60
10
0.2
B
60≤t＜90
16
0.32
C
90≤t＜120
11
0.22
D
120≤t＜150
6
0.12
E
150≤t＜180
a
0.1
F
180≤t＜210
2
0.04
合计
n
1
进价
售价
乒乓球拍（元/套）
a
50
羽毛球拍（元/套）
b
60