备考2024届高考物理一轮复习讲义第十一章磁场第2讲磁场运动电荷的作用考点2带电粒子在有界匀强磁场中的运动

这是一份备考2024届高考物理一轮复习讲义第十一章磁场第2讲磁场运动电荷的作用考点2带电粒子在有界匀强磁场中的运动，共6页。

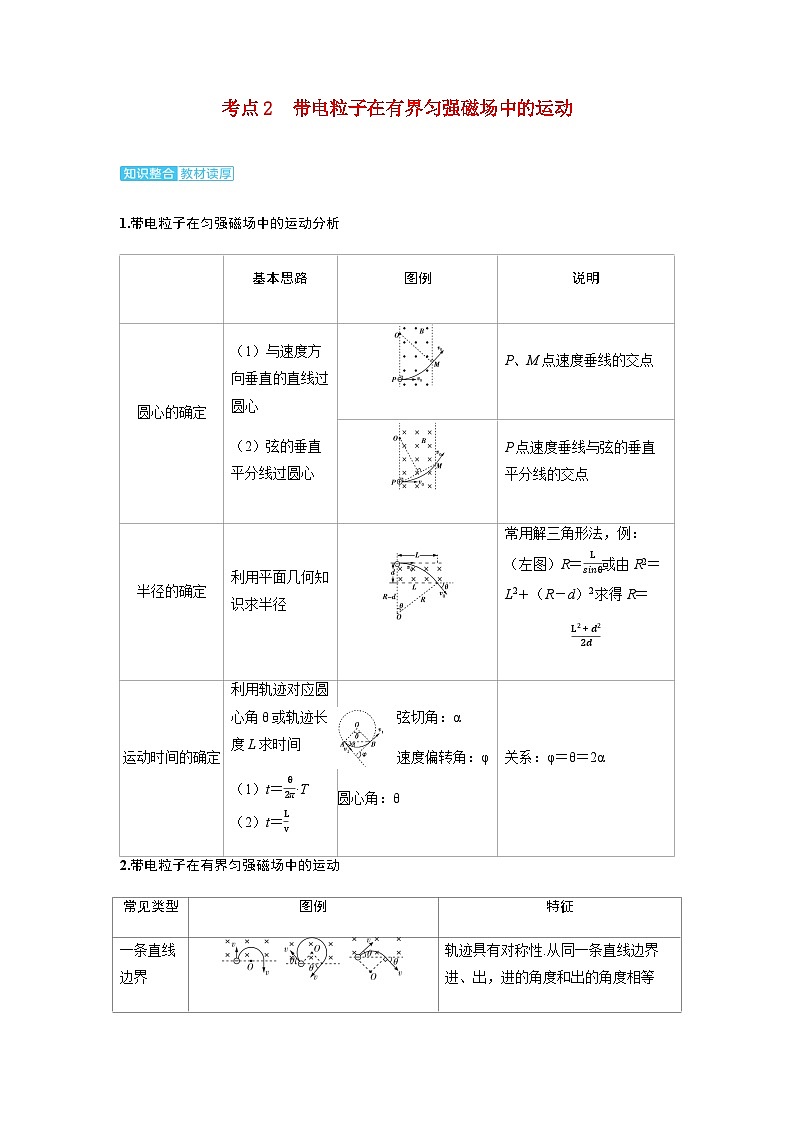
1.带电粒子在匀强磁场中的运动分析
2.带电粒子在有界匀强磁场中的运动
如图所示为洛伦兹力演示仪，当电子枪水平向左发射电子，电子在洛伦兹力作用下做圆周运动，则可判断两励磁线圈中电流方向（从目前的视角观察）（ A ）
A.均为顺时针方向
B.均为逆时针方向
C.靠近观察者的线圈中电流为顺时针方向、另一线圈中电流为逆时针方向
D.靠近观察者的线圈中电流为逆时针方向、另一线圈中电流为顺时针方向
解析 因为电子枪水平向左发射电子，电子在洛伦兹力作用下做圆周运动，受到竖直向上的洛伦兹力，所以由左手定则知磁场方向垂直纸面向里，且两线圈应产生相同方向的磁场，由安培定则知，两线圈中电流方向都为顺时针方向，A正确.
研透高考 明确方向
命题点1 直线边界磁场
6.[多选]如图所示，一单边有界匀强磁场的边界上有一粒子源，以与水平方向成θ角的不同速率向磁场中射入两个相同的粒子1和2，粒子1经磁场偏转后从边界上A点射出磁场，粒子2经磁场偏转后从边界上B点射出磁场，OA＝AB，则（ AC ）
A.粒子1与粒子2的速率之比为1：2
B.粒子1与粒子2的速率之比为1：4
C.粒子1与粒子2在磁场中运动的时间之比为1：1
D.粒子1与粒子2在磁场中运动的时间之比为1：2
解析 粒子1进入磁场时速度的垂线与OA的垂直平分线的交点为粒子1在磁场中做圆周运动的圆心，同理，粒子2进入磁场时速度的垂线与OB的垂直平分线的交点为粒子2在磁场中做圆周运动的圆心，如图所示.由几何关系可知，粒子1与粒子2在磁场中做圆周运动的半径之比为1：2，由r＝mvqB可知，粒子1与粒子2的速率之比为1：2，A正确，B错误；由于粒子在磁场中做圆周运动的周期均为T＝2πmqB，且两粒子在磁场中做圆周运动的轨迹所对的圆心角相同，因此两粒子在磁场中运动的时间相同，即C正确，D错误.
命题点2 矩形和三角形边界磁场
7.[矩形边界]如图，边长为l的正方形abcd内存在匀强磁场，磁感应强度大小为B、方向垂直于纸面（abcd所在平面）向外.ab边中点有一电子发射源O，可向磁场内沿垂直于ab边的方向发射电子.已知电子的比荷为k，则从a、d两点射出的电子的速度大小分别为（ B ）
A.14kBl，54kBB.14kBl，54kBl
C.12kBl，54kBlD.12kBl，54kBl
解析 电子从a点射出时，其轨迹半径为ra＝l4，由洛伦兹力提供向心力，有evaB＝mva2ra，又em＝k，解得va＝kBl4；电子从d点射出时，由几何关系有rd2＝l2＋(rd－l2)2，解得轨迹半径为rd＝5l4，由洛伦兹力提供向心力，有evdB＝mvd2rd，又em＝k，解得vd＝5kBl4，B正确.
8.[三角形边界]如图，在直角三角形OPN区域内存在匀强磁场，磁感应强度大小为B、方向垂直于纸面向外.一带正电的粒子从静止开始经电压U加速后，沿平行于x轴的方向射入磁场；一段时间后，该粒子在OP边上某点以垂直于x轴的方向射出.已知O点为坐标原点，N点在y轴上，OP与x轴的夹角为30°，粒子进入磁场的入射点与离开磁场的出射点之间的距离为d，不计重力.求：
（1）带电粒子的比荷；
（2）带电粒子从射入磁场到运动至x轴的时间.
答案 （1）4UB2d2 （2）Bd24U（π2＋33）
解析 （1）设带电粒子的质量为m，电荷量为q，加速后的速度大小为v.由动能定理有qU＝12mv2 ①
设粒子在磁场中做匀速圆周运动的半径为r，如图所示，由洛伦兹力公式和牛顿第二定律有qvB＝mv2r ②
由几何关系知
d＝2r ③
联立①②③式得qm＝4UB2d2 ④
（2）由几何关系知，带电粒子射入磁场后运动到x轴所经过的路程为s＝πr2＋rtan30° ⑤
带电粒子从射入磁场到运动至x轴的时间为t＝sv ⑥
联立②④⑤⑥式得t＝Bd24U（π2＋33）.
命题点3 圆形边界磁场
9.如图所示，半径为R的圆是一圆柱形匀强磁场区域的横截面（纸面），磁场的磁感应强度大小为B，方向垂直于纸面向外.一电荷量为q（q＞0）、质量为m的粒子沿平行于直径ab的方向射入磁场区域，射入点与ab的距离为R2，已知粒子射入、射出磁场时运动方向间的夹角为60°，则粒子的速率为（不计重力）（ B ）
A.qBR2mB.qBRmC.3qBR2mD.2qBRm
解析 如图所示，粒子做圆周运动的圆心O2必在过入射点垂直于入射速度方向的直线EF上，由于粒子射入、射出磁场时运动方向间的夹角为60°，故圆弧ENM对应的圆心角为60°，所以△EMO2为等边三角形.由于O1D＝R2，由几何关系知∠EO1D＝60°，△O1ME为等边三角形，所以可得到粒子做圆周运动的半径EO2＝O1E＝R，由qvB＝mv2R，得v＝qBRm，B正确.
命题拓展
情境不变，一题多设问
（1）上例中，带电粒子在圆柱形匀强磁场区域中的运动时间为（ B ）
A.πm6qBB.πm3qBC.2πm3qBD.πmqB
解析 粒子在磁场中做圆周运动，转过的圆心角θ＝60°，则在磁场中运动时间t＝θ360°T＝60°360°×2πmqB＝πm3qB，B项正确.
（2）上例中，若带电粒子从a点沿直径ab的方向射入磁场区域，粒子射入、射出磁场时运动方向的夹角仍为60°，则粒子的速率为（ C ）
A.qBR2mB.qBRmC.3qBRmD.2qBRm
解析 由题意，粒子运动轨迹如图1所示，则∠aO2c＝60°，∠aO1c＝120°.由几何关系得r＝3R，又qvB＝mv2r，则v＝qBrm＝3qBRm，C项正确.
（3）上例中，若带电粒子速率不变，磁场方向改为垂直纸面向里，则带电粒子射入、射出磁场时运动方向间的夹角为（ D ）
A.30°B.45°C.60°D.120°
解析 因带电粒子的速率不变，由qvB＝mv2r得r＝R，则粒子运动轨迹如图2所示，由几何关系得∠EO2F＝120°，D项正确.
命题点4 直角边界磁场
10.[2021北京]如图所示，在xOy坐标系的第一象限内存在匀强磁场.一带电粒子在P点以与x轴正方向成60°角的方向垂直磁场射入，并恰好垂直于y轴射出磁场.已知带电粒子质量为m、电荷量为q，OP＝a.不计重力.根据上述信息可以得出（ A ）
A.带电粒子在磁场中运动的轨迹方程
B.带电粒子在磁场中运动的速率
C.带电粒子在磁场中运动的时间
D.该匀强磁场的磁感应强度
解析 如图，找出轨迹圆心O'，画出带电粒子在磁场中做匀速圆周运动的轨迹，利用三角函数知识求出轨迹半径r＝asin60°＝233a，OO'＝atan60°＝33a，则轨迹方程为x2＋(y－33a)2＝43a2(x＞0，y＞0)，故A正确；由洛伦兹力提供向心力有qvB＝mv2r，故v＝qBrm，因为B和v均未知，故B、D错误；因为T＝2πrv＝2πmqB，B未知，不能求出周期T，故不能求出带电粒子在磁场中运动的时间，C错误.
基本思路
图例
说明
圆心的确定
（1）与速度方向垂直的直线过圆心
（2）弦的垂直平分线过圆心
P、M点速度垂线的交点
P点速度垂线与弦的垂直平分线的交点
半径的确定
利用平面几何知识求半径
常用解三角形法，例：（左图）R＝Lsinθ或由R2＝L2＋（R－d）2求得R＝L2＋d22d
运动时间的确定
利用轨迹对应圆心角θ或轨迹长度L求时间
（1）t＝θ2π·T （2）t＝Lv
弦切角：α
速度偏转角：φ
圆心角：θ
关系：φ＝θ＝2α
常见类型
图例
特征
一条直线边界
轨迹具有对称性.从同一条直线边界进、出，进的角度和出的角度相等
两条平行直线边界
圆轨迹的半径与速度有关，所以粒子有可能从同一条直线边界或另一条直线边界射出，其临界条件是圆轨迹与另一条直线边界相切.规范作出圆轨迹图像，利用三角函数或勾股定理求解圆半径R
矩形和三角形边界
由于边界的限制，粒子的运动常常出现临界问题，一般临界的位置在圆轨迹与直线边界相切处
圆形边界
沿径向射入圆形磁场的粒子必沿径向射出，运动具有对称性；不沿径向射入圆形磁场时，粒子射入磁场时速度方向与半径夹角为θ，则粒子射出磁场时速度方向与半径夹角也为θ