






2024年中考数学一轮复习考点突破课件---平面直角坐标系与函数
展开
这是一份2024年中考数学一轮复习考点突破课件---平面直角坐标系与函数,共33页。PPT课件主要包含了知识梳理,全体实数,不等于0,大于或等于0,列表法,图象法,例题讲解,变式练习,x≥-2且x≠0,T=20-2t等内容,欢迎下载使用。
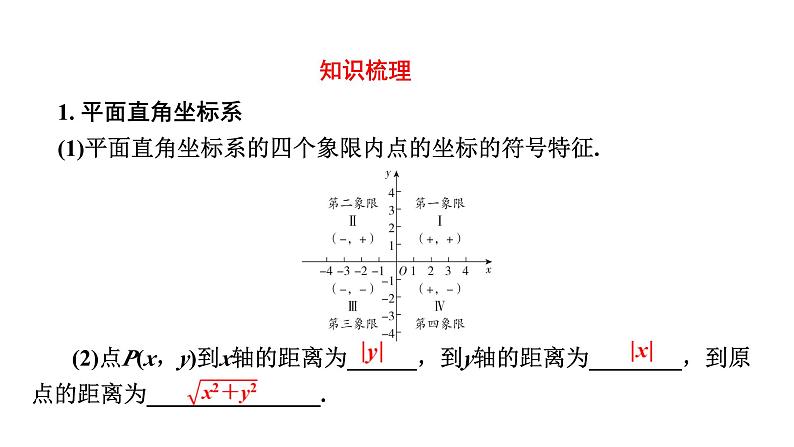
1. 平面直角坐标系(1)平面直角坐标系的四个象限内点的坐标的符号特征.
(2)点P(x,y)到x轴的距离为______,到y轴的距离为________,到原点的距离为_______________.
2. 函数自变量的取值范围(1)当函数解析式是整式时,自变量的取值范围是______________. (2)当函数解析式是分式时,分母________________. (3)当函数解析式是二次根式时,被开方数________________. (4)当函数解析式表示一个实际问题时,自变量的取值范围还必须使实际问题有意义.
3. 表示函数的方法解析式法、________和________. 4. 描点法画函数图象的一般步骤①列表;②________;③________.
1. 在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为( ).A.(-4,5) B.(-5,4)C.(4,-5) D.(5,-4)
考点3.列函数解析式【例3】某加油站的加油机显示器上显示某种油的单价为每升8.25元,总价从0元开始随着加油量的变化而变化,则总价y(单位:元)与加油量x(单位:L)之间的函数解析式是__________. 分析与解答 因为总价=单价×加油量,所以 y=8.25x.规律方法 现实中存在着大量的等量关系,当涉及的是两个变量之间的等量关系时,就可以根据这个等量关系建立函数解析式,清楚地表明其中的变化规律.
3. 冷冻一个20 ℃的物体,若它每小时下降2 ℃,则物体的温度T(单位:℃)与冷冻时间t(单位:h)的函数解析式是______________.
考点4.探究图象信息 【例4】星期日小峰去朋友家借书,他离家的距离y(单位:km)与时间x(单位:min)的函数图象如图所示.根据图象提供的信息,下列说法正确的是( ).
A.小峰去时的速度大于回家的速度B.小峰在朋友家停留了10 minC.小峰去时所花的时间少于回家所花的时间D.小峰去时走上坡路,回家时走下坡路
4. 如图,将一个盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内.现用一个注水管沿大容器内壁匀速注水,则小水杯水面的高度h(单位:cm)与注水时间t(单位:min)的函数图象大致为( ).
一、选择题. 1. 下列曲线,不能表示y是x的函数的是( ).
A B C D
4. 在平面直角坐标系中,点P(x2+2,-3)所在的象限是( ).A.第一象限 B.第二象限C.第三象限 D.第四象限
5. 如图,若在该中国象棋棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“炮”位于点( ).
A.(-2,-1) B.(0,0)C.(1,-2) D.(-1,1)
6. 已知M(-4,a-2),N(-2,a),P(2,a)三点在同一个函数图象上,则这个函数图象可能是( ).
A B
C D
7. 将矩形纸板剪掉一个小矩形后的剩余部分如图①所示,动点P从点A出发,沿路径A→B→C→D→E→F匀速运动,速度为1 cm/s,点P到达终点F后停止运动.△APF的面积S(S≠0,单位:cm2)与点P运动的时间t(单位:s)的关系如图②所示,根据图象得出下列结论:①AF=5 cm;②a=6;③点P从点E运动到点F需要10 s;④矩形纸板裁剪前后周长均为34 cm.其中正确的有( ).
A.4个 B.3个 C.2个 D.1个
10. 为了加强市民的节水意识,某市制定了如下收费标准:每户每月的用水量不超过10 m3时,按每立方米2.2元收费;超过10 m3时,超过的部分按每立方米3.8元收费.某户居民5月份用水x m3(x>10),应缴水费y元,则y与x之间的函数解析式是________________.
y=3.8x-16
11. 观察图中各正方形图案,每条边上有 n(n≥2)个圆点,每个图案中圆点的总数是S.按此规律,可推断出S与n的关系式为______________.
n=2 n=3 n=4S=4 S=8 S=12
三、解答题.12. 已知等腰三角形的周长为12 cm,设底边长为y cm,一腰长为x cm.(1)写出y与x之间的函数解析式.(2)求自变量x的取值范围.
由2x+y=12,得y=12-2x.
由题意得x>0,y>0,且2x>y,即x>0,12-2x>0,且2x>12-2x,解得3<x<6.
13. 甲、乙两位专业自行车手从A地出发,骑自行车沿同一条路行驶到B地.他们离出发地的距离s(单位:km)和行驶时间t(单位:h)之间的关系如图所示.已知甲在途中休息了一段时间,之后他再次骑行的速度是原来的一半.(1)求乙的速度.
(2)求甲在途中休息的时间.(3)两人相遇时,离B地的路程还有多少千米?
1. (2022·广东)水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为C=2πr.下列判断正确的是( ).A.2是变量 B.π是变量C.r是变量 D.C是常量
4. (2022·武汉)匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线).这个容器的形状可能是( ).
A B C D
5. (2023·淄博)下列函数图象中,能反映y的值始终随x值的增大而增大的是( ).
A B
C D
6. (2022·北京)下面的三个问题中都有两个变量:①汽车从A地匀速行驶到B地,汽车的剩余路程y与行驶时间x;②将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;③用长度一定的绳子围成一个矩形,矩形的面积y与一边长x.其中,变量y与变量x之间的函数关系可以利用如图所示的图象表示的是( ).
A.①②B.①③C.②③D.①②③
相关课件
这是一份(经典版)中考数学一轮考点复习精品课件专题3.1 平面直角坐标系与函数 (含解析),共1页。
这是一份专题08 平面直角坐标系与函数课件-数学中考一轮复习,共27页。
这是一份平面直角坐标系及函数-中考数学一轮复习课件,共16页。PPT课件主要包含了坐标轴上点的坐标特征,纵坐标都相等,横坐标都相等,a-b,-ab,-a-b,点平移的坐标特征,x+3y,x-3y,xy+2等内容,欢迎下载使用。









