人教A版 (2019)选择性必修 第三册第八章 成对数据的统计分析8.2 一元线性回归模型及其应用优质ppt课件

这是一份人教A版 (2019)选择性必修 第三册第八章 成对数据的统计分析8.2 一元线性回归模型及其应用优质ppt课件，文件包含821《一元线性回归模型》课件-人教版高中数学选修三pptx、821《一元线性回归模型》分层作业原卷版-人教版高中数学选修三docx、821《一元线性回归模型》分层作业解析版-人教版高中数学选修三docx等3份课件配套教学资源，其中PPT共24页， 欢迎下载使用。

1.结合具体实例，了解一元线性回归模型的含义.2.了解模型参数的统计意义，了解最小二乘原理.
2.相关系数的性质： ① 当r>0时，称成对样本数据正相关；当r<0时，称成对样本数据负相关. ② |r|≤1； ③ 当|r|越接近1时，成对数据的线性相关程度越强；当|r|越接近0时，成对数据的线性相关程度越弱；特别地，当|r|＝0时，成对数据的没有线性相关关系；当|r|＝1时，成对数据都落在一条直线上.
恩格尔系数(Engel’s Cefficient)是根据恩格尔定律得出的比例数，指居民家庭中食物支出占消费总支出的比重，是表示生活水平高低的一个指标．其计算公式：恩格尔系数＝食物支出金额÷总支出金额．
一个家庭收入越少，家庭收入中或者家庭总支出中用来购买食物的支出所占的比例就越大，随着家庭收入的增加，家庭收入中或者家庭支出中用来购买食物的支出所占比例将会下降.问题　恩格尔系数是预测生活水平高低的一个模型，那么当两个变量线性相关时，我们如何对成对样本数据建立一个模型进行预测？提示　为了对两个变量线性相关关系进行预测，我们通常建立一元线性回归模型进行预测．
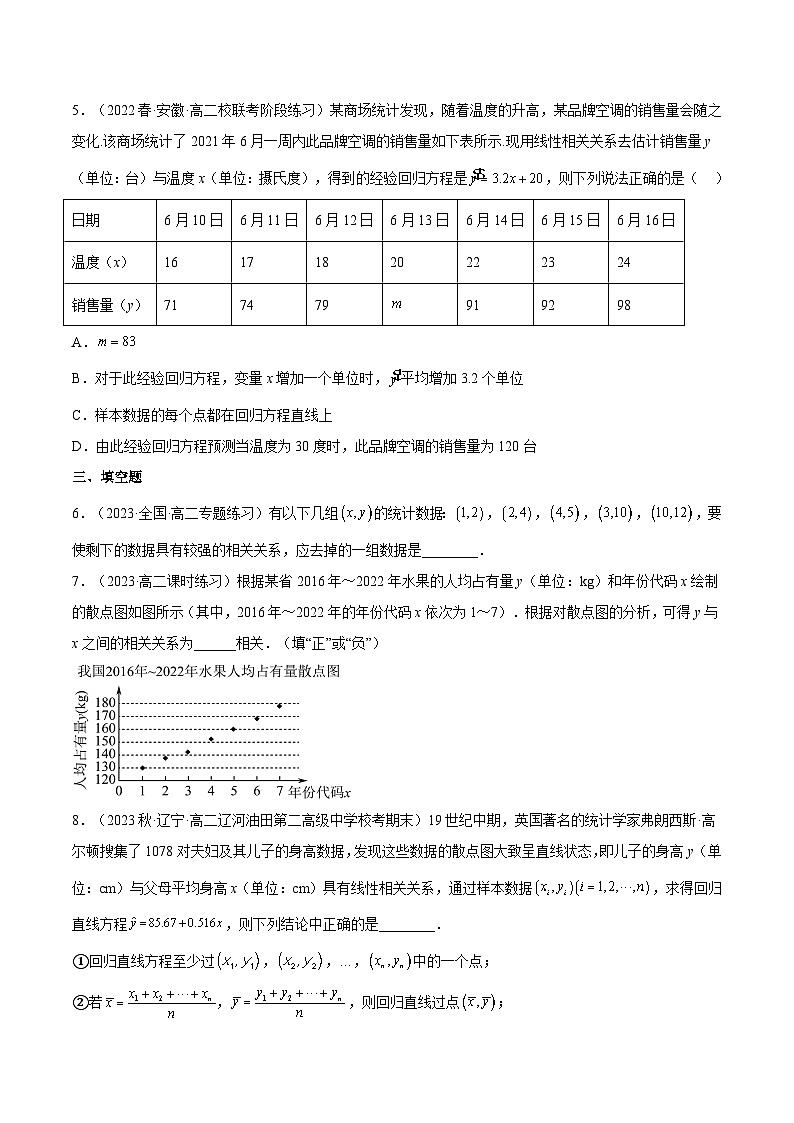
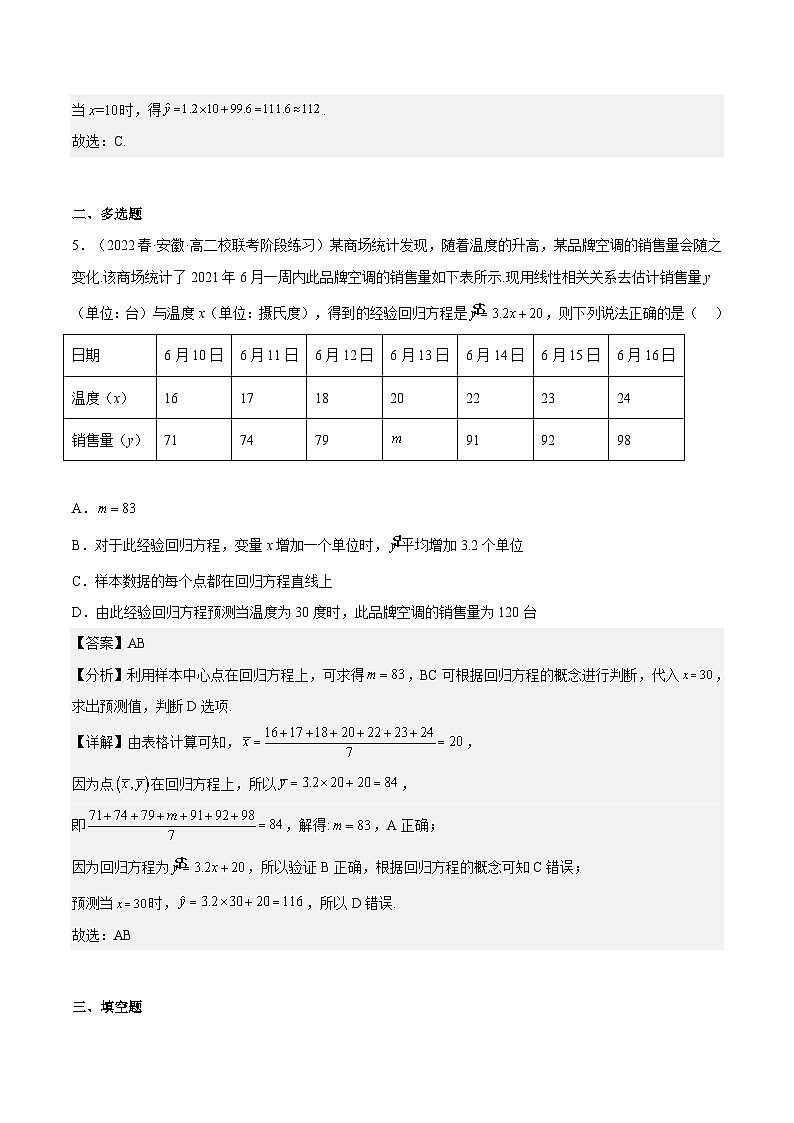
通过前面的学习我们已经了解到，根据成对样本数据的散点图和样本相关系数，可以推断两个变量是否存在相关关系、是正相关还是负相关，以及线性相关程度的强弱等. 进一步地，如果能像建立函数模型刻画两个变量之间的确定性关系那样，通过建立适当的统计模型刻画两个随机变量的相关关系，那么我们就可以利用这个模型研究两个变量之间的随机关系，并通过模型进行预测.下面我们研究当两个变量线性相关时，如何利用成对样本数据建立统计模型，并利用模型进行预测的问题.
生活经验告诉我们，儿子的身高与父亲的身高不仅线性相关，而且还是正相关，即父亲的身高较高时，儿子的身高通常也较高. 为了进一步研究两者之间的关系， 有人调查了14名男大学生的身高及其父亲的身高，得到的数据如下表所示.
利用前面表示数据的方法，以横轴表示父亲身高、纵轴表示儿子身高建立直角坐标系，再将表中的成对样本数据表示为散点图，如右图所示.
由图可知散点大致分布在一条从左下角到右，上角的直线附近，表明儿子身高和父亲身高线性相关. 利用统计软件，求得样本相关系数为r≈0.886，表明儿子身高和父亲身高正线性相关，且相关程度较高.
思考1 根据数据，父子的身高之间的关系可以用函数模型刻画吗?
儿子身高和父亲身高之间不是函数关系，故不能用函数模型刻画. 但由于父子的身高有较强的线性相关，因此我们可以用一次函数来刻画父亲身高对儿子身高的影响，而把影响儿子身高的其他因素作为随机误差，得到刻画两个变量之间关系的线性回归模型. 若用x表示父亲身高，Y表示儿子身高，e表示随机误差. 假定随机误差e的均值为0，方差为与父亲身高无关的定值σ2，则它们之间的关系可以表示为
我们称(1)式为Y关于x的一元线性回归模型. 其中，Y称为因变量或响应变量，x称为自变量或解释变量；a和b为模型的未知参数，a称为截距参数，b称为斜率参数；e是Y与bx+a之间的随机误差. 模型中的Y也是随机变量，其值虽不能由变量x的值确定，但却能表示为bx+a与e的和，前一部分由x所确定，后一部分是随机的. 如果e=0，那么Y与x之间的关系就可用一元线性函数模型来描述.
因为误差是随机的，即取各种正负误差的可能性一样，所以它们均值的理想状态应该为0.
追问1：为什么要假设E(e)=0，而不假设其为某个不为0的常数？
追问2：你能结合父亲与儿子身高的实例，说明回归模型(1)的意义？
追问3：对于父亲身高为xi的某一名男大学生，他的身高yi一定是bxi+a吗？
思考2 结合具体实例解释产生模型(1)中随机误差项的原因吗?
在研究儿子身高与父亲身高的关系时，产生随机误差e的原因有:(1) 除父亲身高外，其他可能影响儿子身高的因素，比如母亲身高、生活环境、饮食习惯和锻炼时间等；(2)在测量儿子身高时，由于测量工具、测量精度所产生的测量误差；(3)实际问题中，我们不知道儿子身高和父亲身高的相关关系是什么，可以利用一元线性回归模型来近似这种关系，这种近似也是产生随机误差e的原因.
在一元线性回归模型y＝bx＋a＋e中，随机误差e产生的原因有： 1. 所用的确定性函数不恰当引起的误差； 2. 忽略了某些因素的影响； 3. 存在观测误差．
例题 若某地财政收入x与支出y满足一元线性回归模型y＝bx＋a＋e(单元：亿元)，其中b＝0.7，a＝3，|e|≤0.5，如果今年该地区财政收入10亿元，年支出预计不会超过多少？
解：因为财政收入x与支出y满足一元线性回归模型y＝bx＋a＋e，其中b＝0.7，a＝3，所以得到 y＝0.7 x＋3＋e，当x＝10时，得y＝0.7×10＋3＋e＝10＋e，而|e|≤0.5，即－0.5≤e≤0.5，所以9.5≤y≤10.5，所以年支出预计不会超过10.5亿元．
1. 说明函数模型与回归模型的区别，并分别举出两个应用函数模型和回归模型的例子.
解：函数模型刻画的是变量之间具有的函数关系，是一种确定性的关系.回归模型刻画的是变量之间具有的相关关系，不是一种确定性的关系，即回归模型刻画的是两个变量之间的随机关系.例如，路程与速度的关系、正方体体积与边长的关系可以应用函数模型刻画；体重与身高的关系、冷饮销量与气温的关系可以应用回归模型刻画.
2. 在一元线性回归模型(1) 中，参数b的含义是什么?
解：参数b的含义可以解释为解释变量x对响应变量Y的均值的影响，变量x每增加1个单位，响应变量Y的均值将增加b个单位. 例如，教科书中父亲身高为175 cm的儿子身高的均值比父亲身高为174cm的儿子身高的均值高出0.839cm.注意：因为响应变量Y最终取值，除了受变量x的影响，还要受随机误差e的影响，所以不能解释成解释变量x每增加一个单位，响应变量Y增加b个单位.
解：不能.一是父亲的身高与儿子的身高之间是随机关系，不是函数关系；二是这组数据仅是总体的一个样本，不一定能很好地描述两个变量之间的关系.
3. 将图8.2-1中的点按父亲身高的大小次序用折线连起来，所得到的图象是一个折线图，可以用这条折线表示儿子身高和父亲身高之间的关系吗？
解析　因为回归直线的斜率为80，所以x每增加1，y平均增加80，即劳动生产率提高1 000元时，工人工资平均提高80元．答案　B
解析　∵两个变量线性负相关，∴变量x增加一个单位，y平均减少1.5个单位．答案　C
4．已知回归直线的斜率的估计值是1.23，且过定点(4，5)，则线性回归方程是__________．
5．某产品的广告费用x(单位：万元)与销售额y(单位：万元)的统计数据如下表：
其中，Y称为因变量或响应变量，x称为自变量或解释变量；a和b为模型的未知参数，a称为截距参数，b称为斜率参数；e是Y与bx+a之间的随机误差.