资料中包含下列文件,点击文件名可预览资料内容













还剩33页未读,
继续阅读
成套系列资料,整套一键下载
人教A版 (2019)8.2 一元线性回归模型及其应用优秀ppt课件
展开
这是一份人教A版 (2019)8.2 一元线性回归模型及其应用优秀ppt课件,文件包含822《一元线性回归模型参数的最小二乘估计》第1课时课件-人教版高中数学选修三pptx、822《一元线性回归模型参数的最小二乘估计》分层作业原卷版-人教版高中数学选修三docx、822《一元线性回归模型参数的最小二乘估计》分层作业解析版-人教版高中数学选修三docx等3份课件配套教学资源,其中PPT共41页, 欢迎下载使用。
1.进一步掌握一元线性回归模型参数的统计意义,会用相关统计软件.2.了解非线性回归模型.3.会通过分析残差和利用R2判断回归模型的拟合效果.
2.一元线性回归模型与函数模型的区别
Y称为因变量或响应变量,
x称为自变量或解释变量,
e是Y与bx+a之间的随机误差.
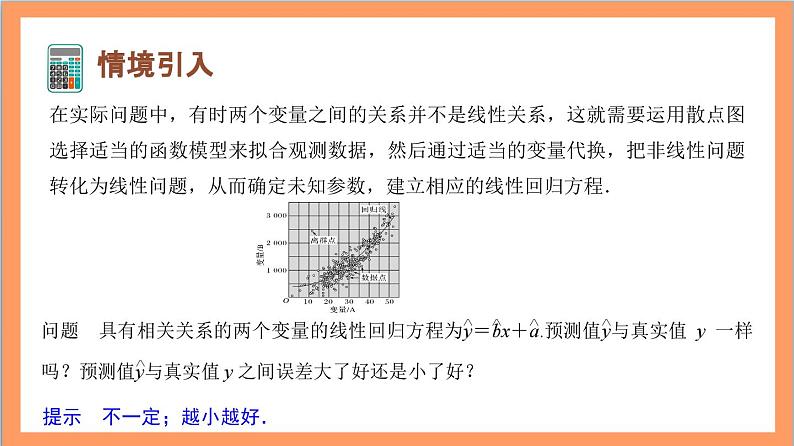
在实际问题中,有时两个变量之间的关系并不是线性关系,这就需要运用散点图选择适当的函数模型来拟合观测数据,然后通过适当的变量代换,把非线性问题转化为线性问题,从而确定未知参数,建立相应的线性回归方程.
提示 不一定;越小越好.
在一元线性回归模型中,表达式Y=bx+a+e刻画的是变量Y与变量x之间的线性相关关系,其中参数a和b未知,需要根据成对样本数据进行估计. 由模型的建立过程可知,参数a和b刻画了变量Y与变量x的线性关系,因此通过成对样本数据估计这两个参数,相当于寻找一条适当的直线,使表示成对样本数据的这些散点在整体上与这条直线最接近.
探究 利用散点图找出一条直线,使各散点在整体上与此直线尽可能接近.
方法一:采用测量的方法,先画出一条直线,测量出各点与它的距离,然后移动直线,到达一个使距离的和最小的位置. 然后测量出此时的斜率和截距,就可得到一 条直线,如图(1)所示.
方法二: 在图中选择这样的两点画直线,使得直线两侧的点的个数基本相同,把这条直线作为所求直线,如图(2)所示.
方法三:在散点图中多取几对点,确定出几条直线的方程,再分别求出这些直线的斜率、截距的平均数,将这两个平均数作为所求直线的斜率和截距,如图(3)所示.
上面这些方法虽然有一定的道理,但比较难操作,我们需要另辟蹊径.先进一步明确我们面临的任务: 从成对样本数据出发,用数学的方法刻画“从整体上看,各散点与直线最接近”.通常,我们会想到利用点到直线y=bx+a的“距离”来刻画散点与该直线的接近程度,然后用所有“距离”之和刻画所有样本观测数据与该直线的接近程度.
设满足一元线性回归模型的两个变量的n对样本数据为(x1, y1), (x2, y2), ‧‧‧, (xn, yn), 由yi=bxi+a+ei (i=1, 2, ‧‧‧, n),得
显然|ei|越小,表示点(xi , yi)与点(xi , bxi+a)的“距离”越小,即样本数据点离直线y=bx+a的竖直距离越小,如右图所示. 特别地,当ei = 0时,表示点(xi , yi)在这条直线上.
在实际应用中,因为绝对值使得计算不方便,所以人们通常用各散点到直线的竖直距离的平方之和
来刻画“整体接近程度”.
所以我们可以取使Q达到最小的a和b的值作为截距和斜率的估计值.
∴要使Q取得最小值,当且仅当b的取值为
综上,当a, b的取值为
经验回归方程与最小二乘估计:
例1 某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
(1) 画出销售额和利润额的散点图;(2) 计算利润额y对销售额x的经验回归直线方程.
解:(1) 散点图如下:
求经验回归方程的步骤:
显然不一定,因为还有其他影响儿子身高的因素,父亲身高不能完全决定儿子身高. 不过,我们可以作出推测,当父亲身高为176cm时,儿子身高一般在177cm左右.实际上,如果把这所学校父亲身高为176cm的所有儿子身高作为一个子总体,那么177cm是这个子总体的均值的估计值.
对于响应变量Y,通过观测得到的数据称为观测值,通过经验回归方程得到的)称为预测值,观测值减去预测值称为残差. 残差是随机误差的估计结果,通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据等,这方面工作称为残差分析.
类似地,我们还可以得到其他的残差,如下表所示.
为了使数据更加直观,用父亲身高作为横坐标,残差作为纵坐标,可以画出残差图,如图下所示.
观判断模型是否满足一元线性回归模型的假设. 一般地,建立经验回归方程后,通常需要对模型刻画数据的效果进行分析.借助残差分析还可以对模型进行改进,使我们能根据改进模型作出更符合实际的预测与决策.
观察残差的散点图可以发现,残差比较均匀地分布在横轴的两边. 说明残差比较符合一元线性回归模型的假定,是均值为0、方差为σ2的随机变量的观测值. 可见,通过观察残差图可以直
思考2 观察下列四幅残差图,你认为哪一个残差满足一元线性回归模型中对随机误差的假定?
通过观察发现,图(4)的残差比较均匀地分布在以取值为0的横轴为对称轴的水平带状区域内. 所以在四幅残差图中,只有图(4)满足一元线性回归模型对随机误差的假设.
例2在某种产品表面进行腐蚀刻线试验,得到腐蚀深度y(μm)与腐蚀时间x(s)之间的一组观察值如表.
(1) 画出散点图;(2) 求y关于x的经验回归方程;(3) 利用经验回归方程预测时间为100 s时腐蚀深度为多少.
解:(1) 散点图如图所示,
∴y关于x的经验回归方程为
1. 对一元线性回归模型参数a和b的估计中,有人认为:“估计方法不止一种,根据不同的样本观测数据到直线‘ 整体接近程度’的定义,可以得到参数a和b不同的估计,只要‘整体接近程度’定义合理即可.”你觉得这个说法对吗?
∴估计女儿的身高为168 cm左右.
解:先画人体的脂肪含量与年龄的散点图,如图(1)所示. 由散点图可以发现人体的脂肪含量与年龄呈现近似线性关系,可以用一元线性回归模型刻画.
3. 根据下表数据,建立人体的脂肪含量关于年龄的经验回归方程,画出残差图,描述残差图的特点.
画残差图,如图(2)所示,通过残差图可以看到,残差比较均匀地分布在横轴的两边. 说明残差比较符合一元线性回归模型对随机误差的假设.
经计算可知残差的总和为0.027. 但是
4. 计算表8.2-2中的所有残差之和,你能发现什么规律?
即理论上残差的总和应等于0,这个误差是由于计算过程中四舍五入的原因导致.
则Q是关于b的二次函数. 要使Q小值,当且仅当b的取值为
1.下列两个变量之间的关系不是函数关系的是( )A.角度和它的余弦值B.正方形的边长和面积C.正n边形的边数和内角度数和D.人的年龄和身高解析 函数关系就是变量之间的一种确定性关系.A,B,C三项中的两个变量之间都是函数关系,可以写出相应的函数表达式,分别为f(θ)=cs θ,g(a)=a2,h(n)=(n-2)π.D选项中的两个变量之间不是函数关系,对于年龄确定的人群,仍可以有不同的身高,故选D.答案 D
2.(多选题)关于残差图的描述正确的是( )A.残差图的横坐标可以是样本编号B.残差图的横坐标也可以是解释变量或预报变量C.残差点分布的带状区域的宽度越窄相关指数越小D.残差点分布的带状区域的宽度越窄残差平方和越小
解析 残差点分布的带状区域的宽度越窄,说明模型拟合精度越高,则残差平方和越小,此时,R2的值越大,故描述错误的是C.答案 ABD
3.某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:
4.在研究硝酸钠的溶解度时,观察它在不同温度(x)的水中溶解度(y)的结果如下表:
由此得到回归直线的斜率是__________.
5.在一次抽样调查中测得样本的5个样本点,数值如下表:
根据散点图可知y与x近似地呈反比例函数关系,
由散点图可以看出y与t呈近似的线性相关关系,列表如下:
1.进一步掌握一元线性回归模型参数的统计意义,会用相关统计软件.2.了解非线性回归模型.3.会通过分析残差和利用R2判断回归模型的拟合效果.
2.一元线性回归模型与函数模型的区别
Y称为因变量或响应变量,
x称为自变量或解释变量,
e是Y与bx+a之间的随机误差.
在实际问题中,有时两个变量之间的关系并不是线性关系,这就需要运用散点图选择适当的函数模型来拟合观测数据,然后通过适当的变量代换,把非线性问题转化为线性问题,从而确定未知参数,建立相应的线性回归方程.
提示 不一定;越小越好.
在一元线性回归模型中,表达式Y=bx+a+e刻画的是变量Y与变量x之间的线性相关关系,其中参数a和b未知,需要根据成对样本数据进行估计. 由模型的建立过程可知,参数a和b刻画了变量Y与变量x的线性关系,因此通过成对样本数据估计这两个参数,相当于寻找一条适当的直线,使表示成对样本数据的这些散点在整体上与这条直线最接近.
探究 利用散点图找出一条直线,使各散点在整体上与此直线尽可能接近.
方法一:采用测量的方法,先画出一条直线,测量出各点与它的距离,然后移动直线,到达一个使距离的和最小的位置. 然后测量出此时的斜率和截距,就可得到一 条直线,如图(1)所示.
方法二: 在图中选择这样的两点画直线,使得直线两侧的点的个数基本相同,把这条直线作为所求直线,如图(2)所示.
方法三:在散点图中多取几对点,确定出几条直线的方程,再分别求出这些直线的斜率、截距的平均数,将这两个平均数作为所求直线的斜率和截距,如图(3)所示.
上面这些方法虽然有一定的道理,但比较难操作,我们需要另辟蹊径.先进一步明确我们面临的任务: 从成对样本数据出发,用数学的方法刻画“从整体上看,各散点与直线最接近”.通常,我们会想到利用点到直线y=bx+a的“距离”来刻画散点与该直线的接近程度,然后用所有“距离”之和刻画所有样本观测数据与该直线的接近程度.
设满足一元线性回归模型的两个变量的n对样本数据为(x1, y1), (x2, y2), ‧‧‧, (xn, yn), 由yi=bxi+a+ei (i=1, 2, ‧‧‧, n),得
显然|ei|越小,表示点(xi , yi)与点(xi , bxi+a)的“距离”越小,即样本数据点离直线y=bx+a的竖直距离越小,如右图所示. 特别地,当ei = 0时,表示点(xi , yi)在这条直线上.
在实际应用中,因为绝对值使得计算不方便,所以人们通常用各散点到直线的竖直距离的平方之和
来刻画“整体接近程度”.
所以我们可以取使Q达到最小的a和b的值作为截距和斜率的估计值.
∴要使Q取得最小值,当且仅当b的取值为
综上,当a, b的取值为
经验回归方程与最小二乘估计:
例1 某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
(1) 画出销售额和利润额的散点图;(2) 计算利润额y对销售额x的经验回归直线方程.
解:(1) 散点图如下:
求经验回归方程的步骤:
显然不一定,因为还有其他影响儿子身高的因素,父亲身高不能完全决定儿子身高. 不过,我们可以作出推测,当父亲身高为176cm时,儿子身高一般在177cm左右.实际上,如果把这所学校父亲身高为176cm的所有儿子身高作为一个子总体,那么177cm是这个子总体的均值的估计值.
对于响应变量Y,通过观测得到的数据称为观测值,通过经验回归方程得到的)称为预测值,观测值减去预测值称为残差. 残差是随机误差的估计结果,通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据等,这方面工作称为残差分析.
类似地,我们还可以得到其他的残差,如下表所示.
为了使数据更加直观,用父亲身高作为横坐标,残差作为纵坐标,可以画出残差图,如图下所示.
观判断模型是否满足一元线性回归模型的假设. 一般地,建立经验回归方程后,通常需要对模型刻画数据的效果进行分析.借助残差分析还可以对模型进行改进,使我们能根据改进模型作出更符合实际的预测与决策.
观察残差的散点图可以发现,残差比较均匀地分布在横轴的两边. 说明残差比较符合一元线性回归模型的假定,是均值为0、方差为σ2的随机变量的观测值. 可见,通过观察残差图可以直
思考2 观察下列四幅残差图,你认为哪一个残差满足一元线性回归模型中对随机误差的假定?
通过观察发现,图(4)的残差比较均匀地分布在以取值为0的横轴为对称轴的水平带状区域内. 所以在四幅残差图中,只有图(4)满足一元线性回归模型对随机误差的假设.
例2在某种产品表面进行腐蚀刻线试验,得到腐蚀深度y(μm)与腐蚀时间x(s)之间的一组观察值如表.
(1) 画出散点图;(2) 求y关于x的经验回归方程;(3) 利用经验回归方程预测时间为100 s时腐蚀深度为多少.
解:(1) 散点图如图所示,
∴y关于x的经验回归方程为
1. 对一元线性回归模型参数a和b的估计中,有人认为:“估计方法不止一种,根据不同的样本观测数据到直线‘ 整体接近程度’的定义,可以得到参数a和b不同的估计,只要‘整体接近程度’定义合理即可.”你觉得这个说法对吗?
∴估计女儿的身高为168 cm左右.
解:先画人体的脂肪含量与年龄的散点图,如图(1)所示. 由散点图可以发现人体的脂肪含量与年龄呈现近似线性关系,可以用一元线性回归模型刻画.
3. 根据下表数据,建立人体的脂肪含量关于年龄的经验回归方程,画出残差图,描述残差图的特点.
画残差图,如图(2)所示,通过残差图可以看到,残差比较均匀地分布在横轴的两边. 说明残差比较符合一元线性回归模型对随机误差的假设.
经计算可知残差的总和为0.027. 但是
4. 计算表8.2-2中的所有残差之和,你能发现什么规律?
即理论上残差的总和应等于0,这个误差是由于计算过程中四舍五入的原因导致.
则Q是关于b的二次函数. 要使Q小值,当且仅当b的取值为
1.下列两个变量之间的关系不是函数关系的是( )A.角度和它的余弦值B.正方形的边长和面积C.正n边形的边数和内角度数和D.人的年龄和身高解析 函数关系就是变量之间的一种确定性关系.A,B,C三项中的两个变量之间都是函数关系,可以写出相应的函数表达式,分别为f(θ)=cs θ,g(a)=a2,h(n)=(n-2)π.D选项中的两个变量之间不是函数关系,对于年龄确定的人群,仍可以有不同的身高,故选D.答案 D
2.(多选题)关于残差图的描述正确的是( )A.残差图的横坐标可以是样本编号B.残差图的横坐标也可以是解释变量或预报变量C.残差点分布的带状区域的宽度越窄相关指数越小D.残差点分布的带状区域的宽度越窄残差平方和越小
解析 残差点分布的带状区域的宽度越窄,说明模型拟合精度越高,则残差平方和越小,此时,R2的值越大,故描述错误的是C.答案 ABD
3.某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:
4.在研究硝酸钠的溶解度时,观察它在不同温度(x)的水中溶解度(y)的结果如下表:
由此得到回归直线的斜率是__________.
5.在一次抽样调查中测得样本的5个样本点,数值如下表:
根据散点图可知y与x近似地呈反比例函数关系,
由散点图可以看出y与t呈近似的线性相关关系,列表如下:













