高中数学人教A版 (2019)选择性必修 第三册第八章 成对数据的统计分析8.2 一元线性回归模型及其应用完整版ppt课件

这是一份高中数学人教A版 (2019)选择性必修 第三册第八章 成对数据的统计分析8.2 一元线性回归模型及其应用完整版ppt课件，文件包含822一元线性回归模型参数的最小二乘估计第2课时课件-人教版高中数学选修三pptx、822《一元线性回归模型参数的最小二乘估计》分层作业原卷版-人教版高中数学选修三docx、822《一元线性回归模型参数的最小二乘估计》分层作业解析版-人教版高中数学选修三docx等3份课件配套教学资源，其中PPT共33页， 欢迎下载使用。

1.进一步掌握一元线性回归模型参数的统计意义，会用相关统计软件.2.了解非线性回归模型.3.会通过分析残差和利用R2判断回归模型的拟合效果.
例 经验表明，一般树的胸径 (树的主干在地面以上1.3m处的直径)越大， 树就越高 . 由于测量树高比测量胸径困难，因此研究人员希望由胸径预测树高 . 在研究树高与胸径之间的关系时，某林场收集了某种树的一些数据如下表，试根据这些数据建立树高关于胸径的经验回归方程.
例 根据下面数据建立树高关于胸径的经验回归方程.
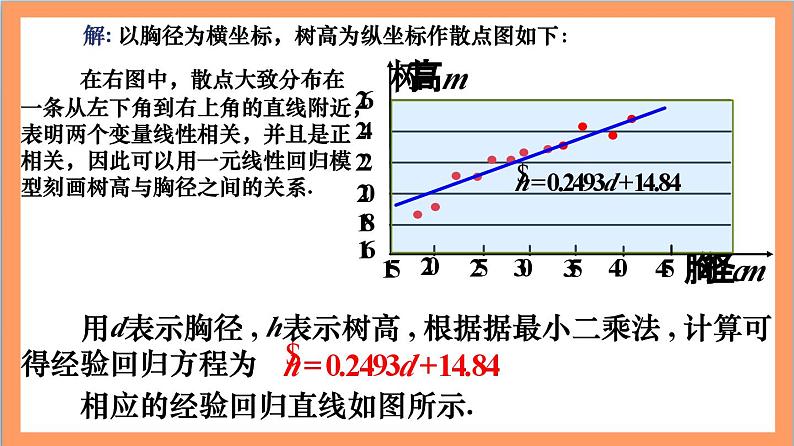
解: 以胸径为横坐标，树高为纵坐标作散点图如下：
在右图中，散点大致分布在一条从左下角到右上角的直线附近，表明两个变量线性相关，并且是正相关，因此可以用一元线性回归模型刻画树高与胸径之间的关系.
用d表示胸径 , h表示树高 , 根据据最小二乘法 , 计算可得经验回归方程为
相应的经验回归直线如图所示.
根据经验回归方程，由胸径的数据可以计算出树高的预测值(精确到0.1)以及相应的残差，如下表所示.
以胸径为横坐标, 残差为纵坐标, 作残差图, 得到下图.
观察残差表和残差图，可以看到，残差的绝对值最大是0.8，所有残差分布在以横轴为对称轴、宽度小于2的带状区域内 . 可见经验回归方程较好地刻画了树高与胸径的关系，我们可以根据经验回归方程由胸径预测树高.
问题 人们常将男子短跑100m的高水平运动员称为“百米飞人”. 下表给出了1968年之前男子短跑100m世界纪录产生的年份和世界纪录的数据. 试依据这些成对数据，建立男子短跑100m世界纪录关于纪录产生年份的经验回归方程.
2. 求经验回归方程：
将经验回归方程叠加到散点图，如图(3)所示.
由图形可知，第一点远离经验回归直线，并且前后两时间段中的散点都在经验回归直线的上方，中间时间段的散点都在经验回归直线的下方. 这说明散点并不是随机分布在经验回归直线的周围，而是围绕着经验回归直线有一定的变化规律，即成对样本数据呈现出明显的非线性相关的特征.
对模型进行修改，以使其更好地反映散点的分布特征.
用上述函数刻画数据变化的趋势，这是一个非线性经验回归函数，其中c1, c2 是待定参数. 现在问题转化为如何利用成对数据估计参数c1和c2.
为了利用一元线性回归模型估计参数c1和c2，我们引进一个中间变量x，令x=ln(t-1895). 通过x=ln(t-1895)，将年份变量数据进行变换，得到新的成对数据(精确到0.01)，如下表所示.
在上图中画出经验回归直线，如图所示.
在同一坐标系中画出成对数据散点图、非线性经验回归方程②的图像(蓝色)以及经验回归方程①的图像(红色)，如图所示.
我们发现，散点图中各散点都非常靠近②的图像, 表明非线性经验回归方程②对于原始数据的拟合效果远远好于经验回归方程①.
下面通过残差来比较这两个经验回归方程对数据刻画的好坏.
用ti表示编号为i的年份数据，用yi表示编号为i的纪录数据，则经验回归方程①和②的残差计算公式分别为
两个经验回归方程的残差(精确到0.001)如下表所示.
观察各项残差的绝对值，发现经验回归方程②远远小于①，即经验回归方程②的拟合效果要远远好于①.
在一般情况下，直接比较两个模型的残差比较困难，因为在某些散点上一个模型的残差的绝对值比另一个模型的小，而另一些散点的情况则相反. 可以通过比较残差的平方和来比较两个模型的效果. 由
可知Q2小于Q1. 因此在残差平方和最小的标准下，非线性回归模型
的拟合效果要优于一元线性回归模型的拟合效果.
通过前面的讨论我们知道，当残差的平方和越小，经验回归模型的拟合效果就越好，故我们可以用决定系数R2来验证模型的拟合效果.决定系数R2的计算公式为
决定系数是总偏差平方和中回归平方和所占的比重. 显然0≤R2≤1，R2越接近1，则线性回归刻画的效果越好.还可以证明，在一元线性回归模型中R2=r2，即决定系数R2等于响应变量与解释变量的样本相关系数r的平方.
由上述残差表可算出经验回归方程①和②的决定系数R2分别为
在使用经验回归方程进行预测时,需注意以下问题
1.回归方程只适用于我们所研究的样本的总体；
2.我们所建立的回归方程一般都有时间性；
3.样本采集的范围会影响回归方程的适用范围；
4.不能期望回归方程得到的预报值就是预报变量的精确值. 事实上, 它是预报变量的可能取值的平均值.
1. 在回归分析中，分析残差能够帮助我们解决哪些问题?
解：分析残差可以帮助我们解决以下几个问题: (1) 寻找残差明显比其他残差大很多的异常点，如果有，检查相应的样本数据是否有错. (2) 分析残差图可以诊断选择的模型是否合适，如果不合适，可以参考残差图提出修改模型的思路.
(1)作GDP和年份的散点图，根据该图猜想它们之间的关系可以用什么模型描述；
2. 1997-2006 年我国的国内生产总值(GDP)的数据如下:
解：(1) 画GDP与年份的散点图，如图所示，可以观察到随着年份的增加GDP也随之增加，GDP值与年份呈现近似线性关系，可以用一元线性回归模型刻画.
(2) 建立年份为解释变量, GDP为响应变量的一元线性回归模型, 并计算残差;(3) 根据你得到的一元线性回归模型，预测2017年的GDP，看看你的预测值与实际的GDP的误差是多少;
(3) 2017年的GDP预报值为359684亿元，2017年的实际的GDP为820754亿元，预测值比实际值少461070亿元.
(4) 你认为这个模型能较好地刻画GDP和年份的关系吗? 请说明理由.
解：(4)上面建立的回归方程的R2=0.9213，说明在1997-2006 年内，该模型年份能够解释92.13%的GDP值变化，因此所建立的模型较好地刻画了GDP和年份的关系. 但因为残差呈现一定的规律性，中间是负数，两边是正数，所以可以考虑用非线性回归模型拟合数据.
(5)随着时间的发展，又收集到2007-2016年的GDP数据如下:
建立年份(1997-2016)为解释变量，GDP为响应变量的经验回归方程，并预测2017年的GDP，与实际的GDP误差是多少? 你能发现什么?
1.某班5名学生的数学和物理成绩如下表：(1)画出散点图；(2)求物理成绩y对数学成绩x的经验回归方程；(3)一名学生的数学成绩是96，试预测他的物理成绩．
解　(1)散点图如图．
2.为研究重量x(单位：克)对弹簧长度y(单位：厘米)的影响，对不同重量的6个物体进行测量，数据如下表所示：(1)作出散点图并求线性回归方程；(2)求出R2；(3)进行残差分析．
解　(1)数据对应的散点图如右图所示：
(3)由残差表中的数值可以看出第3个样本点的残差比较大，需要确认在采集这个数据的时候是否有人为的错误，如果有的话，需要纠正数据，重新建立回归模型；由表中数据可以看出残差点比较均匀地落在不超过0.15的狭窄的水平带状区域中，说明选用的线性回归模型的精度较高，由以上分析可知，弹簧长度与拉力成线性关系．
3.判断模型拟合的效果: 残差分析
R2越大，模型的拟合效果越好, R2越小，模型拟合效果越差.