高中人教A版 (2019)第一章 空间向量与立体几何1.3 空间向量及其运算的坐标表示获奖作业ppt课件

这是一份高中人教A版 (2019)第一章 空间向量与立体几何1.3 空间向量及其运算的坐标表示获奖作业ppt课件，文件包含131《空间直角坐标系》课件-人教版高中数学选修一pptx、131《空间直角坐标系》分层作业原卷版-人教版高中数学选修一docx、131《空间直角坐标系》分层作业解析版-人教版高中数学选修一docx等3份课件配套教学资源，其中PPT共29页， 欢迎下载使用。

02空间直角坐标系中点的坐标
1.学会空间直角坐标系的建立方法2.掌握空间中一点的坐标表示3.掌握空间向量的坐标表示．
学习了空间向量基本定理，建立了“空间基底”的概念，我们就可以利用基底表示任意一个空间向量，进而把空间向量的运算转化为基向量的运算．所以，基底概念的引人为几何问题代数化奠定了基础.
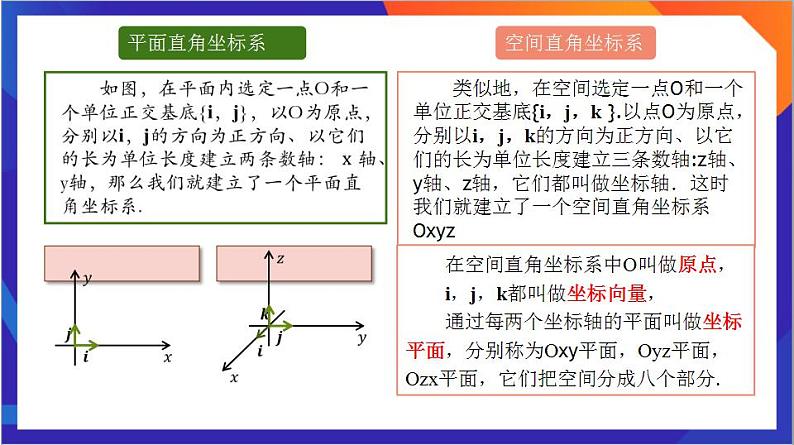
类似地，在空间选定一点O和一个单位正交基底{i，j，k }.以点О为原点，分别以i，j，k的方向为正方向、以它们的长为单位长度建立三条数轴:z轴、y轴、z轴，它们都叫做坐标轴．这时我们就建立了一个空间直角坐标系Oxyz
在空间直角坐标系中O叫做原点，i，j，k都叫做坐标向量，通过每两个坐标轴的平面叫做坐标平面，分别称为Oxy平面，Oyz平面，Ozx平面，它们把空间分成八个部分.
画空间直角坐标系Ozyz时，一般使∠xOy =135°(或45°)，∠yOz=90°.在空间直角坐标系中，让右手拇指指向x轴的正方向，食指指向y轴的正方向，如果中指指向z轴的正方向，则称这个坐标系为右手直角坐标系．本书建立的坐标系都是右手直角坐标系.
在平面直角坐标系中，每一个点和向量都可用一对有序实数（即它的坐标）表示．对空间直角坐标系中的每一个点和向量，是否也有类似的表示呢?
空间直角坐标系中一些特殊的点
1.空间直角坐标系中坐标轴、坐标平面上的点的坐标
2.空间直角坐标系中对称点的坐标（关于谁对称,谁保持不变,其余坐标相反）
(1)点(a,b,c)关于原点O的对称点为(-a,-b,-c);(2)点(a,b,c)关于x轴的对称点为(a,-b,-c);(3)点(a,b,c)关于y轴的对称点为(-a,b,-c);(4)点(a,b,c)关于z轴的对称点为(-a,-b,c);(5)点(a,b,c)关于Oxy平面的对称点为(a,b,-c);(6)点(a,b,c)关于Oyz平面的对称点为(-a,b,c);(7)点(a,b,c)关于Ozx平面的对称点为(a,-b,c).
用坐标表示空间向量的步骤如下:
1.在空间直角坐标系中标出下列各点:A(0,2,4)，B(1,0,5)， C(0,2,0)，D(1,3,4).
解析：1.解析建立如图所示的空间直角坐标系,表示各点如图.
2.在空间直角坐标系Oxyz中,(1)哪个坐标平面与x轴垂直？哪个坐标平面与y轴垂直？哪个坐标平面与z轴垂直？(2)写出点P(2,3,4)在三个坐标平面内的射影的坐标(3)写出点P(1,3,5)关于原点成中心对称的点的坐标