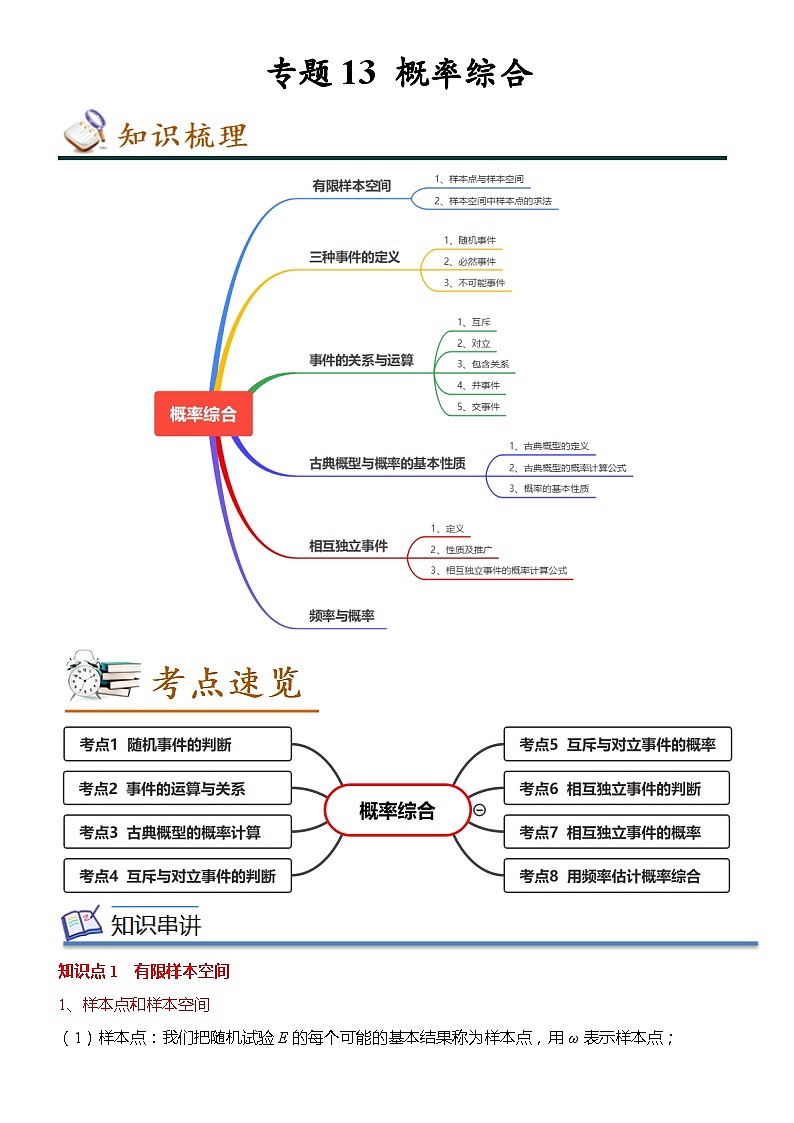
专题13 概率综合（知识串讲+热考题型+专题训练）-2023-2024学年高一数学下学期期中期末考点大串讲（人教A版2019必修第二册）

这是一份专题13 概率综合（知识串讲+热考题型+专题训练）-2023-2024学年高一数学下学期期中期末考点大串讲（人教A版2019必修第二册），文件包含专题13概率综合原卷版docx、专题13概率综合解析版docx等2份试卷配套教学资源，其中试卷共53页， 欢迎下载使用。

知识点1 有限样本空间
1、样本点和样本空间
（1）样本点：我们把随机试验E的每个可能的基本结果称为样本点，用ω表示样本点；
（2）样本空间：全体样本点的集合称为试验E的样本空间，用Ω表示样本空间；
（3）有限样本空间：如果一个随机试验有n个可能结果ω1，ω2，…，ωn，则称样本空间Ω＝{ω1，ω2，…，ωn}为有限样本空间，Ω＝{ω1，ω2，…，ωn}
2、样本空间中样本点的求法
（1）列举法：也称枚举法，对于一些情境比较简单，样本点个数不是很多的概率问题，计算时只需要一一列举，即可得出随机事件所包含的言本店，注意列举时必须按一定的顺序，做到不重不漏。
（2）列表法：碎玉样本点个数不是太多的情况，可以采用列表法。通常把对问题的思考分析归结为“有序实数对”，以便更直接地得到样本点个数，列表法的有点是准确、全面、不易遗漏，期中最常用的方法是坐标系法。
（3）树状图法：树状图适用于按一顺序排雷的较复杂问题中言本店个数的求解，是一种常用的方法。
知识点2 三种事件的定义
1、随机事件：我们将样本空间Ω的子集称为随机事件，简称事件，并把只包含一个样本点的事件称为基本事件．随机事件一般用大写字母A，B，C，…表示．在每次试验中，当且仅当A中某个样本点出现时，称为事件A发生；
2、必然事件：Ω作为自身的子集，包含了所有的样本点，在每次试验中总有一个样本点发生，所以Ω总会发生，我们称Ω为必然事件；
3、不可能事件：空集∅不包含任何样本点，在每次试验中都不会发生，我们称∅为不可能事件。
注意：判断一个事件是哪类事件要看两点
一看条件：因为三种事件都是相对于一定条件而言的；
二看结果是否发生：一定发生的是必然事件，不一定发生的是随机事件，
一定不发生的是不可能事件．
知识点3 事件的关系与运算
1.互斥（互不相容）：一般地，如果事件A与事件B不能同时发生，
也就是说A∩B是一个不可能事件，即A∩B＝∅，
则称事件A与事件B互斥(或互不相容)
2、互为对立：一般地，如果事件A与事件B在任何一次试验中有且仅有一个发生，
即A∪B＝Ω，且A∩B＝∅，那么称事件A与事件B互为对立．
事件A的对立事件记为eq \(A,\s\up6(－))
3、包含关系：一般地，若事件A发生，则事件B一定发生，
我们就称事件B包含事件A(或事件A包含于事件B)，
即B ⊇A(或A⊆B)，
特殊情形：如果事件B包含事件A，事件A也包含事件B，即B⊇A且A⊆B，
则称事件A与事件B相等，记作A＝B
4、并事件（和事件）：一般地，事件A与事件B至少有一个发生，
这样的事件中的样本点或者在事件A中，或者在事件B中，
则称这个事件为事件A与事件B的并事件(或和事件) A∪B(或A＋B)
5、交事件（积事件）：一般地，事件A与事件B同时发生，
这样的一个事件中的样本点既在事件A中，也在事件B中，
则称这样的事件为事件A与事件B的交事件(或积事件) A∩B(或AB)
知识点4 古典概型与概率的基本性质
1、古典概型的定义
我们将具有以下两个特征的试验称为古典概型试验，
其数学模型称为古典概率模型，简称古典概型．
（1）有限性：样本空间的样本点只有有限个；
（2）等可能性：每个样本点发生的可能性相等．
2、古典概型的概率计算公式
一般地，设试验E是古典概型，样本空间Ω包含n个样本点，事件A包含其中k个样本点，
则定义事件A的概率P(A)＝eq \f(k,n)＝eq \f(nA,nΩ)，
其中n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数．
3、概率的基本性质
性质1：对任意的事件A，都有P(A)≥0.
性质2：必然事件的概率为1，不可能事件的概率为0，即P(Ω)＝1，P(∅)＝0.
性质3：如果事件A与事件B互斥，那么P(A∪B)＝P(A)＋P(B)．
性质4：如果事件A与事件B互为对立事件，那么P(B)＝1－P(A)，P(A)＝1－P(B)．
性质5：如果A⊆B，那么P(A) ≤P(B)．
性质6：设A，B是一个随机试验中的两个事件，我们有P(A∪B)＝ P(A)＋P(B)－P(A∩B)．
知识点5 相互独立事件
1、定义：对任意两个事件A与B，如果成立，则称事件A与事件B相互独立，简称为独立．
2、性质及推广：
如果事件A与事件B相互独立，则与，与，与也都相互独立。
两个事件的相互独立可以推广到个事件的相互独立性，即若事件相互独立，则这个事件同时发生的概率
3、相互独立事件的概率计算公式
已知两个事件A，B相互独立，它们的概率分别为P(A)，P(B)，则有
知识点6 频率与概率
1、频率的稳定性
大量的试验证明，在任何确定次数的随机试验中，一个随机事件A发生的频率具有随机性.
一般地，随着试验次数n的增大，频率偏离概率的幅度会缩小，即事件A发生的频率fn(A)会逐渐稳定于事件A发生的概率P(A)，我们称频率的这个性质为频率的稳定性.
因此我们可以用频率fn(A)估计概率P(A).
2、频率的求法
频率是事件A发生的次数m与试验总次数n的比值，利用此公式可求出它们的频率，
频率本身是随机变量，当n很大时，频率总是在一个稳定值附近摆动，这个稳定值是概率．
3、频率和概率区别和联系
区别：
（1）在相同的条件下重复n次试验，观察某一事件A是否出现，称n次试验中事件A出现的次数nA为事件A出现的频数，称事件A出现的比例fn(A)＝eq \f(nA,n)为事件A出现的频率．
（2）概率是度量随机事件发生的可能性大小的量
（3）频率是一个变量，随着试验次数的变化而变化，概率是一个定值，是某事件的固有属性．
联系：
对于给定的随机事件A，由于事件A发生的频率fn(A)随着试验次数的增加稳定于概率P(A)，
因此可以用频率fn(A)来估计概率P(A)．
考点1 随机事件的判断
【例1】（2023·高一课时练习）在欧几里得几何中，下列事件中，不可能事件是（ ）
A．三角形的内角和为 B．三角形中大角对大边，小角对小边
C．三角形中任两边之和大于第三边 D．锐角三角形中两内角和小于
【答案】D
【解析】∵三角形的内角和为，∴其为必然事件，故A错误；
∵三角形中大角对大边，小角对小边，∴其为必然事件，故B错误；
∵三角形中任两边之和大于第三边，∴其为必然事件，故C错误；
∵锐角三角形中两内角和大于，
∴“锐角三角形中两内角和小于”为不可能事件，故D正确.故选：D.
【变式1-1】（2023·全国·高三对口高考）给出下列四种说法：
①“三个球全部放入两个盒子，其中必有一个盒子有一个以上的球”是必然事件；
②“当x为某一实数时可使”是不可能事件；
③“从100个灯泡中取出5个，5个都是次品”是随机事件；
④从装有8个红球，6个白球的袋中任取2球，事件“至少有一个白球”和“都是红球”是两个对立事件；
其中不正确说法的个数是（ ）
A．0 B．1 C．2 D．3
【答案】A
【解析】①“三个球全部放入两个盒子，其中必有一个盒子有一个以上的球”正确，
所以是必然事件；故①正确；
②不存在，使，“当x为某一实数时，可使”是不可能事件；故②正确；
③“从100个灯泡中取出5个，5个都是次品”可能发生，也可能不发生，
所以是随机事件；故③正确；
④根据对立事件的定义，可知事件“至少有一个白球”的对立事件是一个白球都没有，
即都是红球，故④正确；故选：A
【变式1-2】（2023·全国·高一专题练习）下列事件中，是不可能事件的是（ ）
A．买一张电影票，座位号是奇数 B．射击运动员射击一次，命中9环
C．明天会下雨 D．度量三角形的内角和，结果是360°
【答案】D
【解析】不可能事件：在条件S下，一定不会发生的事件，叫相对于条件S的不可能事件；
由于三角形内角和为180°，故D项对应的事件是不可能事件，
ABC选项中对应的事件是随机事件，不符合题意.故选：D
【变式1-3】（2023春·全国·高一专题练习）12个同类产品中，有10个正品，任意抽取3个产品概率是1的事件是（ ）
A．3个都是正品 B．至少有一个是次品
C．3个都是次品 D．至少有一个是正品
【答案】D
【解析】因为所求事件的概率是1，所以该事件为必然事件，
对于A，因为可能发生任取出来的3个产品含有次品的情况，
所以事件“3个都是正品”是随机事件，故A错误；
对于B，因为可能发生任取出来的3个产品都是正品的情况，
所以事件“至少有一个是次品”是随机事件，故B错误；
对于C，因为次品的个数只有2个，所以事件“3个都是次品”是不可能事件，故C错误；
对于D，因为次品的个数只有2个，所以任取出来的3个产品必然至少有一个是正品，
即事件“至少有一个是正品”是必然事件，故D正确.故选：D.
【变式1-4】（2023·江苏·高一专题练习）已知集合A是集合B的真子集，则下列关于非空集合A，B的四个命题：
①若任取，则是必然事件；
②若任取，则是不可能事件；
③若任取，则是随机事件；
④若任取，则是必然事件．
其中正确的命题有（ ）
A．1个 B．2个 C．3个 D．4个
【答案】C
【解析】因为集合A是集合B的真子集，所以集合A中的元素都在集合B中，
集合B中存在元素不是集合A中的元素，作出其韦恩图如图：
对于①：集合A中的任何一个元素都是集合B中的元素，任取，
则是必然事件，故①正确；
对于②：任取，则是随机事件，故②不正确；
对于③：因为集合A是集合B的真子集，
集合B中存在元素不是集合A中的元素，
集合B中也存在集合A中的元素，
所以任取，则是随机事件，故③正确；
对于④：因为集合A中的任何一个元素都是集合B中的元素，
任取，则是必然事件，故④正确；
所以①③④正确，正确的命题有3个．故选：C．
考点2 事件的运算与关系
【例2】（2023·全国·高一专题练习）打靶次，事件表示“击中发”，其中、、、.那么表示（ ）
A．全部击中 B．至少击中发 C．至少击中发 D．以上均不正确
【答案】B
【解析】所表示的含义是、、这三个事件中至少有一个发生，
即可能击中发、发或发.故选：B.
【变式2-1】（2023·全国·高一专题练习）甲、乙两个元件构成一并联电路，设E=“甲元件故障”，F=“乙元件故障”，则表示电路故障的事件为（ ）
A．EF B．EF C．E D．
【答案】B
【解析】因为甲、乙两个元件构成一并联电路，
所以只有当甲、乙两个元件都故障时，才造成电路故障，
所以表示电路故障的事件为.故选：B
【变式2-2】（2023·全国·高一专题练习）抛掷一枚骰子，“向上的点数是1或2”为事件，“向上的点数是2或3”为事件，则（ ）
A．
B．
C．表示向上的点数是1或2或3
D．表示向上的点数是1或2或3
【答案】C
【解析】由题意，可知，
则，∴表示向上的点数为1或2或3．故选：C.
【变式2-3】（2022秋·湖北随州·高二随州市曾都区第一中学校考开学考试）（多选）一个袋子中有大小和质地相同的4个球，其中有2个红色球（标号为1和2），2个绿色球（标号为3和4），从袋中不放回地依次随机摸出2个球，每次摸出一个球，设事件“第一次摸到红球”，“两次都摸到红球”，“两次都摸到绿球”，“两球颜色相同”，“两球颜色不同”，则（ ）
A． B． C． D．
【答案】CD
【解析】对于A，因“第一次摸到红球”，“两次都摸到红球”，则，A不正确；
对于B，“两次都摸到红球”，“两次都摸到绿球”，
两个事件没有公共的基本事件，，B不正确；
对于C，“两次都摸到红球”，“两次都摸到绿球”，“两球颜色相同”，
R或G表示摸的两个球的颜色相同，即，C正确；
对于D，“两球颜色相同”，“两球颜色不同”，
由对立事件的定义知，D正确.故选：CD
【变式2-4】（2023·全国·高一专题练习）盒子里有大小和质地均相同的6个红球和4个白球现从中任取3个球，设事件{3个球中有1个红球2个白球}，事件{3个球中有2个红球、1个白球}，事件{3个球中至少有1个红球}，事件{3个球中既有红球又有白球}.
（1）事件D与A，B是什么运算关系？
（2）事件C与A的交事件是什么事件？
【答案】（1）（2）
【解析】设“从10个球中任取3个球,得到i个红球”为事件.
（1）由题意得,事件3个球中有1个红球、2个白球，
事件3个球中有2个红球、1个白球，
事件3个球中既有红球又有白球，
由此可得.
（2）事件3个球中至少有1个红球，
事件3个球中有1个红球、2个白球,.
考点3 古典概型的概率计算
【例3】（2023·高一课时练习）掷一枚骰子三次，所得点数之和为的概率是（ ）
A． B． C． D．
【答案】B
【解析】掷一枚骰子三次，所有的基本事件个数为，
其中，事件“掷一枚骰子三次，所得点数之和为”所包含的基本事件有、
、、、、、、、、
、、、、、、、、
、、、、、、、、
、，共个基本事件，
因此，所求概率为.故选：B.
【变式3-1】（2023春·高一课时练习）围棋起源于中国，据先秦典籍《世本》记载：“尧造围棋，丹朱善之”，围棋至今已有四千多年历史，蕴含者中华文化的丰富内涵.在某次国际比赛中，中国派出包含甲、乙在内的5位棋手参加比赛，他们分成两个小组，其中一个小组有3位，另外一个小组有2位，则甲和乙不在同一个小组的概率为（ ）
A． B． C． D．
【答案】C
【解析】由题意，另3位棋手分别记为丙、丁、戊，
则这5位棋手的分组情况有（甲乙丙，丁戊），（甲乙丁，丙戊），（甲乙戊，丙丁），
（甲丙丁，乙戊），（甲丙戊，乙丁），（甲丁戊，乙丙），（乙丙丁，甲戊），
（乙丙戊，甲丁），（乙丁戊，甲丙），（丙丁戊，甲乙），共10种，
其中甲和乙不在同一个小组的情况分别为（甲丙丁，乙戊），（甲丙戊，乙丁），
（甲丁戊，乙丙），（乙丙丁，甲戊），（乙丙戊，甲丁），（乙丁戊，甲丙），共有6种，
所以甲和乙不在同一个小组的概率.故选：C.
【变式3-2】（2023春·高一课时练习）小林打算从冰壶、短道速滑、花样滑冰、冬季两项这四个项目中任意选两项进行系统的学习，则小林没有选择冰壶的概率为（ ）
A． B． C． D．
【答案】C
【解析】记冰壶、短道速滑、花样滑冰、冬季两项分别为A，B，C，D，
则从这四个项目中任意选两项的情况有AB，AC，AD，BC，BD，CD，共6种，
其中没有选择冰壶的有BC，BD，CD，共3种，
所以所求概率为.故选：C.
【变式3-3】（2023·江苏·高一专题练习）田忌赛马的故事每个人都耳熟能详，众所周知，田忌的上等马优于齐王的中等马，劣于齐王的上等马；田忌的中等马优于齐王的下等马，劣于齐王的中等马；田忌的下等马劣于齐王的下等马．假设田忌与齐王有上等、中等、下等马各一匹，现从双方的马匹中各随机选一匹进行一场比赛，则田忌的马获胜的概率为（ ）
A． B． C． D．
【答案】A
【解析】依题意，记田忌的上等马、中等马、下等马分别为，，，
齐王的上等马、中等马、下等马分别为，，.
由题意可知，可能的比赛有方案有：
，，，，，，，，，共9种，
其中田忌可以获胜的事件为，，，共3种，
则田忌的马获胜的概率为.故选：A.
【变式3-4】（2023·高一课时练习）某学校成立了数学、英语、音乐3个课外兴趣小组，3个小组分别有39，32，33名成员，一些成员参加了不止1个小组，具体情况如图所示．随机选取一名成员．

（1）他参加至少2个小组的概率是多少？
（2）他参加不超过2个小组的概率是多少？
【答案】（1）；（2）
【解析】（1）从图中可以看出，3个课外兴趣小组总人数为60．
用A表示事件“选取的成员只参加1个小组”，
则就表示“选取的成员参加至少2个小组”，于是．
因此，随机选取的一名成员参加至少2个小组的概率是．
（2）用B表示事件“选取的成员参加3个小组”，
则就表示“选取的成员参加不超过2个小组"，
于是，
所以随机选取一名成员属于不超过2个小组的概率是．
考点4 互斥与对立事件的判断
【例4】（2023春·全国·高一专题练习）从装有两个红球和两个黑球的口袋里任取两个球，那么互斥而不对立的两个事件是（ ）
A．“至少有一个黑球”与“都是黑球” B．“至少有一个黑球”与“至少有一个红球”
C．“恰好有一个黑球”与“恰好有两个黑球” D．“至少有一个黑球”与“都是红球”
【答案】C
【解析】当两个球都为黑球时， “至少有一个黑球”与“都是黑球”同时发生，
故A中的两个事件不互斥；
当两个球一个为黑，一个为红时，“至少有一个黑球”与 “至少有一个红球”同时发生，
故B中的两个事件不互斥；
“恰好有一个黑球”与“恰好有两个黑球”不可能同时发生，但有可能同时不发生，
故C中两个事件互斥而不对立；
“至少有一个黑球”与“都是红球”不可能同时发生，但必然有一种情况发生，
故D中两个事件对立．故选：C．
【变式4-1】（2023秋·四川遂宁·高二统考期末）抛掷一枚质地均匀的骰子，记事件A为“落地时向上的点数是奇数”，事件B为“落地时向上的点数是偶数”，事件C为“落地时向上的点数是3的倍数”，事件D为“落地时向上的点数是1或3”，则下列每对事件是互斥事件但不是对立事件的是（ ）
A．A与B B．B与D C．A与D D．B与C
【答案】B
【解析】对选项A：事件和是对立事件，错误；
对选项B：事件和是互斥事件但不是对立事件，正确；
对选项C：事件和不是互斥事件，错误；
对选项D：事件和不是互斥事件，错误；故选：B
【变式4-2】（2022秋·陕西西安·高二陕西师大附中校考阶段练习）从40张扑克牌(红桃、黑桃、方块、梅花点数从1-10各10张)中任取一张：①“抽出红桃”与“抽出黑桃”是对立事件；②“抽出红色牌”与“抽出黑色牌”是互斥事件；③“抽出的牌的数字为5的倍数”与“抽出的牌的数字大于9”是互斥事件；④“抽出数字为2”与“抽出数字为9”是互斥事件；⑤“抽出红色牌”与“抽出黑色牌”是对立事件.其中正确的个数为（ ）
A．1个 B．2个 C．3个 D．4个
【答案】C
【解析】对于①：因为有四种花色，所以“抽出红桃”与“抽出黑桃”是互斥而不对立.故①错误；
对于②：“抽出红色牌”与“抽出黑色牌”是互斥事件.故②正确；
对于③：如果抽出的是“10”，即是“抽出的牌的数字为5的倍数”，
又“抽出的牌的数字大于9”.故③错误；
对于④：抽出的牌的数字不可能是2又是9，
所以“抽出数字为2”与“抽出数字为9”是互斥事件.故④正确；
对于⑤：因为红桃、方块是属于红色牌，黑桃、、梅花是属于黑色牌，
所以抽出的一张牌不是红色就是黑色，
所以“抽出红色牌”与“抽出黑色牌”是对立事件.故⑤正确.
所以正确的说法有3个.故选：C
【变式4-3】（2023春·福建莆田·高二莆田一中校考期中）袋子中有6个大小质地相同的球，其中3个红球，3个黄球，从中不放回随机取出3个球，则概率大于0且与事件“至多取出一个黄球”互斥不对立的事件可以是__________.
【答案】取出2个黄球（答案不唯一）
【解析】由题意，6个球，3个红球，3个黄球，不放回随机取三球，
事件“至多取出一个黄球”的对立事件为“至少取出2个黄球”，
所以概率大于0且与事件“至多取出一个黄球”互斥不对立的事件
可以是“取出2个黄球”或“取出3个黄球”.
故答案为：取出2个黄球（答案不唯一）.
【变式4-4】（2023·高一课时练习）从装有2个红球和2个白球的口袋内任取2个球，那么互斥而不对立的两个事件是（ ）
A．至少有1个白球，都是白球 B．至少有1个白球，至少有1个红球
C．恰有1个白球，恰有2个白球 D．至少有1个白球，都是红球
【答案】C
【解析】设两个红球为红1，红2，两个白球为白1，白2，
由题可知，（红1，红2），（红1，白1），（红1，白2），（红2，白1），
（红2，白2），（白1，白2），
对于A：设2个球中至少有1个白球为事件，则（红1，白1），（红1，白2），
（红2，白1），（红2，白2），（白1，白2），
设2个球都是白球为事件，则（白1，白2），
因为，所以，即事件和不是互斥事件，故A错误；
对于B：设2个球至少有1个红球为事件，则（红1，红2），（红1，白1），
（红1，白2），（红2，白1），（红2，白2），
因为（红1，白1），（红1，白2），（红2，白1），（红2，白2），
所以事件和不是互斥事件，故B错误；
对于C：设2个球中恰有1个白球为事件，则（红1，白1），（红1，白2），
（红2，白1），（红2，白2），
2个球中恰有2个白球为事件，即（白1，白2），
因为，所以事件和互斥，
因为（红1，白1），（红1，白2），（红2，白1），（红2，白2），（白1，白2），
所以事件和不是对立事件，故C正确；
对于D：设2个球都是红球为事件，则（红1，红2），
2个球中至少有1个白球为事件，即（红1，白1），（红1，白2），（红2，白1），
（红2，白2），（白1，白2），
因为，所以事件和是互斥事件，
又因为，所以事件和是对立事件，故D错误，故选：C．
考点5 互斥与对立事件的概率
【例5】（2023·全国·高一专题练习）保险柜的密码由0，1，2，3，4，5，6，7，8，9中的四个数字组成，假设一个人记不清自己的保险柜密码，只记得密码全部由奇数组成且按照递增顺序排列，则最多输入2次就能开锁的概率是（ ）
A． B． C． D．
【答案】C
【解析】密码全部由奇数组成且按照递增顺序排列的结果有：，
，共5个，它们等可能，
最多输入2次就能开锁的事件A，它是输入1次能开锁的事件，
第2次输入才能开锁的事件的和，它们互斥，
，，则，
最多输入2次就能开锁的概率是.故选：C
【变式5-1】（2023·全国·高一专题练习）若事件为两个互斥事件，且，有以下四个结论，其中正确的结论是（ ）
①
②
③
④
A．①③④ B．②③④ C．①②④ D．①②③
【答案】A
【解析】事件为两个互斥事件，，，故①正确；
事件为两个互斥事件，则，，故②错误；
，故③正确；
，故④正确，
综上，①③④正确，故选：A．
【变式5-2】（2023·高一课时练习）某台电话机在打进的电话中响第1声时被接的概率为，响第2声时被接的概率为，响第3声时被接的概率为，若电话在前4声内被接的概率为，则电话在响第4声时被接的概率为多少？
【答案】
【解析】设“电话响第声时被接”为事件，
则，，，这四个事件彼此互斥，
从而有．
即，得．
故电话在响第4声时被接的概率为．
【变式5-3】（2021·高一课时练习）某班级有45%的学生喜欢打羽毛球，80%学生喜欢打乒乓球；两种运动都喜欢的学生有30%.现从该班随机抽取一名学生，求以下事件的概率：
（1）只喜欢打羽毛球；
（2）至少喜欢以上一种运动；
（3）只喜欢以上一种运动；
（4）以上两种运动都不喜欢.
【答案】（1）0.15；（2）0.95；（3）0.65；（4）0.05
【解析】（1）设：A＝“喜欢打羽毛球”，B＝“喜欢打乒乓球”

只喜欢打羽毛球：
（2）至少喜欢以上一种运动：＝
（3）只喜欢以上一种运动：＝
（4）以上两种运动都不喜欢：＝
【变式5-4】（2023·全国·高一专题练习）从1~30这30个整数中随机选择一个数，设事件M表示选到的数能被2整除，事件N表示选到的数能被3整除．求下列事件的概率：
（1）这个数既能被2整除也能被3整除；
（2）这个数能被2整除或能被3整除；
（3）这个数既不能被2整除也不能被3整除．
【答案】（1）；（2）；（3）
【解析】（1）1~30这30个整数中既能被2整除也能被3整除的有5个，∴；
（2）1~30这30个整数中能被2整除的有15个，能被3整除的有10个，
所以，，
；
（3）由于事件“这个数既不能被2整除也不能被3整除”与
事件“这个数能被2整除或能被3整除”互为对立事件，
则．
考点6 相互独立事件的判断
【例6】（2023·全国·高一专题练习）有6个大小相同的小球，其中1个黑色，2个蓝色，3个红色．采用放回方式从中随机取2次球，每次取1个球，甲表示事件“第一次取红球”，乙表示事件“第二次取蓝球”，丙表示事件“两次取出不同颜色的球”，丁表示事件“与两次取出相同颜色的球”，则（ ）
A．甲与乙相互独立 B．甲与丙相互独立
C．乙与丙相互独立 D．乙与丁相互独立
【答案】A
【解析】依题意，事件甲的概率，事件乙的概率，
有放回取球两次的试验的基本事件总数是，
显然事件丙与丁是对立事件，两次取出的球颜色相同含有的基本事件数为，
事件丙的概率，事件丁的概率，
对于A，事件甲与乙同时发生所含的基本事件数为6，
其概率，甲与乙相互独立，A正确；
对于B，事件甲与丙同时发生所含的基本事件数为9，
其概率，甲与丙不独立，B错误；
对于C，事件乙与丙同时发生所含的基本事件数为8，
其概率，乙与丙不独立，C错误；
对于D，事件乙与丁同时发生所含的基本事件数为4，
其概率，乙与丁不独立，D错误.故选：A
【变式6-1】（2023·高一单元测试）下列各对事件中，不互为相互独立事件的是（ ）
A．甲､乙两运动员各射击一次，事件“甲射中10环”，事件“乙射中9环”
B．甲组3名男生，2名女生；乙组2名男生，3名女生，现从甲､乙两组中各选1名学生参加演讲比赛，事件“从甲组中选出1名男生”，事件“从乙组中选出1名女生”
C．袋中有3白､2黑共5个大小相同的小球，依次有放回地摸两球，事件“第一次摸到白球”，事件"第二次摸到白球”
D．袋中有3白､2黑共5个大小相同的小球，依次不放回地摸两球，事件“第一次摸到白球”，事件“第二次摸到黑球”
【答案】D
【解析】对于选项A：甲、乙两运动员各射击一次，甲的成绩与乙的成绩互不影响，
故事件与事件为相互独立事件；
对于选项B：从甲､乙两组中各选1名学生参加演讲比赛，
甲的选择与乙的选择互不影响，故事件与事件为相互独立事件；
对于选项C：依次有放回地摸两球，则第一次的结果与第二次的结果互不影响，
故事件与事件为相互独立事件；
对于选项D：依次不放回地摸两球，则第一次的结果会影响第二次的结果，
故事件与事件不为相互独立事件；故选：D.
【变式6-2】（2023·江苏·高一专题练习）（多选）连续抛掷一枚质地均匀的骰子两次，记录每次的点数，设事件 “第一次出现2点”，“第二次的点数小于5点”，“两次点数之和为奇数”，“两次点数之和为9”，则下列说法正确的有（ ）
A．与不互斥且相互独立 B．与互斥且不相互独立
C．与互斥且不相互独立 D．与不互斥且相互独立
【答案】ABD
【解析】对于A：连续抛掷一枚质地均匀的骰子两次，第一次与第二次的结果互不影响，
即与相互独立；
第一次出现2点，第二次的点数小于5点可以同时发生，与不互斥；故A正确；
对于B：连续抛掷一枚质地均匀的骰子两次，第一次的结果会影响两次点数之和，
即与不相互独立；
第一次出现2点，则两次点数之和最大为8，即与不能同时发生，
即与互斥，故B正确；
对于C：连续抛掷一枚质地均匀的骰子两次，第二次的结果会影响两次点数之和，
即与不相互独立；
若第一次的点数为5，第二次的点数4点，则两次点数之和为9，
即与可以同时发生，即与不互斥，故C错误；
对于D：连续抛掷一枚质地均匀的骰子两次，
第一次的结果不会影响两次点数之和的奇偶，即与相互独立；
若第一次的点数为2，第二次的点数3点，则两次点数之和为5是奇数，
即与可以同时发生，即与不互斥，故D正确.故选：ABD.
【变式6-3】（2023·全国·高一专题练习）（多选）一个装有8个球的口袋中，有标号分别为1，2的2个红球和标号分别为1，2，3，4，5，6的6个蓝球，除颜色和标号外没有其他差异．从中任意摸1个球，设事件“摸出的球是红球”，事件“摸出的球标号为偶数”，事件“摸出的球标号为3的倍数”，则（ ）
A．事件A与事件C互斥
B．事件B与事件C互斥
C．事件A与事件B相互独立
D．事件B与事件C相互独立
【答案】ACD
【解析】对AB，若摸得的球为红球，则其标号为1或2，不可能为3的倍数，
故事件A与事件C互斥，故A正确；
若摸得的球的标号为6，则该标号为3的倍数，故事件B与事件C不互斥，故B错误；
对C，，所以C正确；
对D，，所以D正确；故选：ACD．
【变式6-4】（2023春·全国·高一专题练习）（多选）连续两次抛掷一枚质地均匀的骰子，观察这两次骰子出现的点数．记事件A为“第一次骰子出现的点数为3”，事件B为“第二次骰子出现的点数为5”，事件C为“两次点数之和为8”，事件D为“两次点数之和为7”，则（ ）
A．A与B相互独立 B．A与D相互独立
C．B与C为互斥事件 D．C与D为互斥事件
【答案】ABD
【解析】连续两次抛掷一枚质地均匀的骰子的结果用有序数对表示，
其中第一次在前，第二次在后，不同结果如下：
．共36个．
依题意，，
事件C包括，共5个，，
事件D包括，共6个，．
对于选项A，事件只有结果，
A与B相互独立，所以选项A正确；
对于选项B，事件只有结果，
A与D相互独立，所以选项B正确；
对于选项C，当第一次的点数是3点，第二次是5点时，两个事件同时发生了，
所以事件不是互斥事件，所以选项C不正确；
对于选项D，事件是不可能事件，即C与D是互斥事件，所以选项D正确．
故选：ABD
考点7 相互独立事件的概率
【例7】（2023·江苏·高一专题练习）A，B两名学生均打算只去甲、乙两个城市中的一个上大学，且两人去哪个城市互不影响，若A去甲城市的概率为0.6，B去甲城市的概率为0.3，则A，B不去同一城市上大学的概率为（ ）
A．0.3 B．0.46 C．0.54 D．0.7
【答案】C
【解析】设事件“A去甲城市”，事件“B去甲城市”，
则,,
则A，B不去同一城市上大学的概率为.
故选:C.
【变式7-1】（2023·高一课时练习）甲、乙两名考生填报志愿，要求甲、乙只能在A，B，C这3所院校中选择一所填报志愿．假设每位同学选择各个院校是等可能的，则院校A，B至少有一所被选择的概率为_________．
【答案】
【解析】设事件为院校A，B至少有一所被选择，则其对立事件为两人均选择院校，
甲选择院校的概率为，乙选择院校的概率为，
则甲乙同时选择院校的概率为，
则.
则院校A，B至少有一所被选择的概率为.
故答案为：.
【变式7-2】（2022春·云南·高一统考期末）农历八月十五是我国的传统佳节-中秋节，赏月是中秋节的传统活动之一，如果天晴则可赏月.根据天气预报，中秋节甲地天晴的概率是0.8，乙地天晴的概率是0.9，假定在这段时间内两地是否天晴相互之间没有影响，则至少有一个地方可以赏月的概率为_______________.
【答案】/
【解析】记甲地天晴为事件A，乙地天晴为事件B.
则，
所以至少有一个地方可以赏月的概率为.
故答案为：
【变式7-3】（2023·江苏·高一专题练习）在2022年卡塔尔世界杯决赛中，阿根廷队通过点球大战击败法国队，最终获得世界杯冠军.某游戏公司据此推出了一款“AR点球大战”的游戏，规则如下：游戏分为进攻方和防守方，进攻方最多连续点球5次，若进球则进攻方得1分，若没进则防守方得1分，先得3分者获胜，本次游戏结束.已知某用户作为进攻方时，若某次点球进球，则下次进球的概率为；若没有进球，则下次进球的概率为，在某次游戏中，该用户第1次点球没进，则该用户获胜的概率为________.
【答案】
【解析】该用户第1次点球没进球且该用户获胜可分为点球4次后获胜或点球5次后获胜，
记事件该用户第1次点球没进球且点球4次后获胜，
该用户第1次点球没进球且点球5次后获胜.
若第1次点球没进球且点球4次后获胜，
则只有一种情况，第2次、第3次和第4次均进球，所以；
若第1次点球没进球且点球5次后获胜，则共有3种情况，
①第2次没进，第3次、第4次和第5次进球；
②第3次没进，第2次、第4次和第5次进球；
③第4次没进，第2次、第3次和第5次进球，
所以.
故该用户获胜的概率为.
故答案为：.
【变式7-4】（2023春·全国·高一专题练习）某足球俱乐部举办新一届足球赛,按比赛规则,进入淘汰赛的两支球队如果在120分钟内未分出胜负,则需进行点球大战.点球大战规则如下:第一阶段,双方各派5名球员轮流罚球,双方各罚一球为一轮,球员每罚进一球则为本方获得1分,未罚进不得分,当分差拉大到即使落后一方剩下的球员全部罚进也不能追上的时候,比赛即宣告结束,剩下的球员无需出场罚球.若5名球员全部罚球后双方得分一样,则进入第二阶段,双方每轮各派一名球员罚球,直到出现某一轮一方罚进而另一方未罚进的局面,则罚进的一方获胜.设甲、乙两支球队进入点球大战,由甲队球员先罚球,甲队每位球员罚进点球的概率均为,乙队每位球员罚进点球的概率均为.假设每轮罚球中,两队进球与否互不影响,各轮结果也互不影响.
（1）求每一轮罚球中,甲、乙两队打成平局的概率;
（2）若在点球大战的第一阶段,甲队前两名球员均得分而乙队前两名球员均未得分,甲队暂时以2:0领先,求甲队第5个球员需出场罚球的概率.
【答案】（1）；（2）
【解析】（1）设每一轮罚球中,甲队球员罚进点球的事件为,未罚进点球的事件为;乙队球员罚进点球的事件为,未罚进点球的事件为.
设每一轮罚球中,甲、乙两队打成平局的事件为C,
由题意,得在每一轮罚球中两队打成平局的情况有两种:
甲、乙均未罚进点球,或甲、乙均罚进点球,
则,
故每一轮罚球中,甲、乙两队打成平局的概率为.
（2）因为甲队第5个球员需出场罚球,则前四轮罚球甲、乙两队分差不能超过1分，
即四轮罚球结束时比分可能为2:1或2:2或3:2.
①比分为2:1的概率为
.
②比分为2:2的概率为.
③比分为3:2的概率为
.
综上,甲队第5个球员需出场罚球的概率为.
考点8 用频率估计概率综合
【例8】（2023·高一课时练习）下列说法中正确的个数是（ ）
（1）概率反映随机事件发生的可能性大小；
（2）做次随机试验，事件发生次，则事件发生的频率就是事件发生的概率；
（3）频率是不能脱离次试验的试验值，而概率是具有确定性的不依濑于试验次数的理论值；
（4）在大量的重复试验中，频率是概率的近似值，而概率是频率的稳定值．
A．1 B．2 C．3 D．4
【答案】C
【解析】概率反映随机事件发生的可能性大小，故（1）正确；
做次随机试验，事件发生次，
则事件发生的频率是事件发生的概率的近似值，故（2）不正确；
频率是不能脱离次试验的试验值，而概率是具有确定性的不依濑于试验次数的理论值，
故（3）正确；
在大量的重复试验中，频率是概率的近似值，而概率是频率的稳定值，故（4）正确.
故选：C
【变式8-1】（2023春·全国·高一专题练习）某篮球运动员在最近几次参加的比赛中的得分情况如下表（没有罚球）：
记该运动员在一次投篮中，投中两分球为事件A，投中三分球为事件B，没投中为事件C，用频率估计概率的方法，得到的下述结论中不正确的是（ ）
A．P(A)=0.55 B．P(B)=0.18 C．P(C)=0.27 D．P(B＋C)=0.55
【答案】D
【解析】依题意，，
，
所以D选项结论不正确.故选：D
【变式8-2】（2023·高一课时练习）从存放号码分别为1，2，，10的卡片的盒子中，有放回地取100次，每次取一张卡片并记下号码，统计结果如下：
则取到号码为奇数的频率是（ ）
A．0.53 B．0.5 C．0.47 D．0.37
【答案】A
【解析】由题意知，
∵有放回地取100次，每次取一张卡片并记下号码，
∴总次数是100，
由表可以看出取到号码为奇数有13＋5＋6＋18＋11＝53种结果，
所以频率，故选：A．
【变式8-3】（2023·全国·高一专题练习）某汽车品牌为了了解客户对于其旗下的五种型号汽车的满意情况，随机抽取了一些客户进行回访，调查结果如下表：
其中，满意率是指某种型号汽车的回访客户中，满意人数与总人数的比值．
（1）从Ⅲ型号汽车的回访客户中随机选取1人，求这个客户不满意的概率；
（2）从所有客户中随机选取1个人，估计这个客户满意的概率．
【答案】（1）；（2）
【解析】（1）由表中数据知，Ⅲ型号汽车的回访客户的满意率为0.6，
则从Ⅲ型号汽车的回访客户中随机选取1人，
这个客户不满意的概率为．
（2）由题意知，回访客户的总人数是，
回访客户中满意的客户人数是
，
所以回访客户中客户的满意率为，
所以从所有客户中随机选取1个人，估计这个客户满意的概率约为．
1．（2023·高一课时练习）先后抛掷两颗骰子，设出现的点数之和是12，11，10的概率依次是，，，则（ ）
A． B． C． D．
【答案】B
【解析】先后抛掷两枚骰子，出现的点数共有：
（1，1），（1，2），（1，3），（1，4），（1，5），（1，6），
（2，1），（2，2），（2，3），（2，4），（2，5），（2，6），
（3，1），（3，2），（3，3），（3，4），（3，5），（3，6），
（4，1），（4，2），（4，3），（4，4），（4，5），（4，6），
（5，1），（5，2），（5，3），（5，4），（5，5），（5，6），
（6，1），（6，2），（6，3），（6，4），（6，5），（6，6），共36种，
其中点数之和是12的有1种，故
点数之和是11的有2种，故
点数之和是10的有3种，故
所以，故选：B．
2．（2023·高一课时练习）从不包括大小王的52张扑克牌中随机抽取一张，取到红心的概率为，则没有取到红心的概率为（ ）
A． B． C． D．1
【答案】C
【解析】设：取到红心为事件A，，则没有取到红心是A的对立事件，
；故选：C.
3．（2023·高一单元测试）某人射击一次，成绩记录环数均为整数．设事件：“中靶”；事件：“击中环数大于5”；事件：“击中环数大于1且小于6”；事件：“击中环数大于0且小于6”．则正确的关系是（ ）
A．与为对立事件 B．与为互斥事件
C．与为对立事件 D．与为互斥事件
【答案】D
【解析】当击中环数大于0且小于6时，与同时发生了，不是互斥事件，
更不是对立事件，故选项A B错误；
与显然为互斥事件，当击中环数为时，与都不发生，
故与不是对立事件，故选项C错误；选项D正确.故选：D
4．（2023春·高一课时练习）若，，，则事件A与B的关系是（ ）
A．互斥但不对立 B．对立 C．相互独立 D．既互斥又独立
【答案】C
【解析】∵，∴，
∴，
∴事件A与B相互独立，
题中事件A与B之间没有任何关系，它们既不互斥也不对立.故选：C．
5．（2023·高一课时练习）某校为了增强学生的记忆力和辨识力，组织了一场PK赛，A，B两队各由4名选手组成，每局两队各派一名选手的PK．比赛4局，除第三局胜者得2分外，其余各局胜者均得1分，每局的负者均得0分．假设每局比赛A队选手获胜的概率均为，且各局比赛结果相互独立，比赛结束时A队的得分高于B队的得分的概率为（ ）
A． B． C． D．
【答案】A
【解析】比赛结束时A队的得分高于B队的得分的情况有3种：
A队全胜，A队三胜一负，A队第三局胜另外三局一胜两负，
∴比赛结束时A队的得分高于B队的得分的概率为：
.故选：A．
6．（2023春·高一课时练习）给出下列命题，其中说法正确的是（ ）
A．若A，B为两个随机事件，则
B．若事件A，B，C两两互斥，则
C．若A，B为互斥事件，则
D．若，则
【答案】C
【解析】对于A选项：当A，B为两个互斥事件时，才有，所以A选项错误；
对于B选项：当事件A，B，C两两互斥，且时，
才有，所以B选项错误；
对于C选项：当A，B为互斥事件时，，所以C选项正确；
对于D选项：由概率的性质可知，若，则，所以D选项错误；
故选：C.
7．（2023·全国·高一专题练习）两个黑帮帮主甲和乙决定以如下方式决斗：甲带了一名手下A ，而乙带了两名手下和，规定任意一名手下向敌方成员开枪时，会随机命中敌方的一个尚未倒下的人，且命中每个人的概率相等，并且，三名手下被命中一次之后就会倒下，而甲被命中三次后倒下，乙被命中两次后倒下，只要甲或者乙任意一人倒下，决斗立刻结束，未倒下的一人胜出.决斗开始时，A先向敌方成员开枪，之后若B未倒下，则B向敌方成员开枪，之后按C，A，B，C，A，B，……的顺序依次进行，则甲最终获胜的概率是（ ）
A． B． C． D．
【答案】A
【解析】对于甲来说，一旦唯一一名手下 A被击毙，则甲方必败，同理，若乙方B、
C两名手下被击毙，则乙方必败(题目定义开枪顺序是三名手下轮流开枪，
甲与乙不参与开枪)，按照被击中的顺序表示事件，易知甲获胜的方式有如下几种：
乙甲甲乙，B甲C，C甲B，B甲乙甲，C甲乙甲，事件概率分别记为，
则，，，
，，
所以甲最终获胜的概率是,故选：A
8．（2023春·高一课时练习）下列说法正确的是（ ）
A．当A，B不互斥时，可由公式计算的概率
B．A，B同时发生的概率一定比A，B中恰有一个发生的概率小
C．若，则事件A与B是对立事件
D．事件A，B中至少有一个发生的概率一定比A，B中恰有一个发生的概率大
【答案】A
【解析】根据概率的性质可知，当A，B不互斥时，，
故A中说法正确.
对于两个不可能事件来说，同时发生的概率与恰有一个发生的概率相等，均为零，
故B中说法错误.
在条件下，事件与事件不一定互斥，
故事件A与B不一定是对立事件，故C错误；故C中说法错误.
当事件与事件互斥时，则事件，中
至少有一个发生的概率与，中恰有一个发生的概率相等，故D错误；故选：A.
9．（2023·全国·高一专题练习）（多选）设，是两个随机事件，则下列说法正确的是（ ）
A．表示两个事件至少有一个发生
B．表示两个事件至少有一个发生
C．表示两个事件均不发生
D．表示两个事件均不发生
【答案】ACD
【解析】因为，是两个随机事件，
所以表示两个事件至少有一个发生，故A正确；
表示两个事件恰有一个发生，故B错误；
表示两个事件均不发生，故C正确；
表示两个事件均不发生，故D正确.故选：ACD.
10．（2021秋·高一课时练习）（多选）一个不透明的袋中装有黑、白两种颜色的球各三个，现从中任意取出两个球.设事件P表示“取出的球都是黑球”，事件Q表示“取出的球都是白球”，事件R表示“取出的球中至少有一个黑球”，则下列结论错误的是（ ）
A．P和R是互斥事件
B．P和Q是对立事件
C．Q和R是对立事件
D．Q和R是互斥事件，但不是对立事件
【答案】ABD
【解析】袋中装有黑、白两种颜色的球各三个，现从中取出两个球，
取球的方法有如下几种:①取出的两球都是黑球;
②取出的两球都是白球;③取出的两球一黑一白.
事件R包括①③两种情况，∴事件P是事件R的子事件，故A中结论不正确;
事件Q与事件R互斥且对立，故C中结论正确，D中结论不正确;
事件P与事件Q互斥，但不对立，故B中结论不正确.故选：ABD.
11．（2023春·高一课时练习）（多选）在一次随机试验中，事件发生的概率分别是0.2，0.3，0.5，则下列说法错误的是（ ）
A．与是互斥事件，也是对立事件 B．是必然事件
C． D．
【答案】ABC
【解析】由事件，，不一定两两互斥，所以,
，且，
所以不一定是必然事件，无法判断与是不是互斥或对立事件，
所以A、B、C中说法错误.故选：ABC.
12．（2023·全国·高一专题练习）（多选）已知某养老院75岁及以上的老人占60%．75岁以下的老人中，需要有人全天候陪同的占10%；75岁及以上的老人中，需要有人全天候陪同的占30%．如果从该养老院随机抽取一位老人，则以下结论中，正确的是（ ）
A．抽到的老人年龄在75岁以下的概率为35%
B．抽到的老人需要有人全天候陪同的概率为22%
C．抽到的老人年龄在75岁以下且需要有人全天候陪同的概率为4%
D．抽到的老人年龄大于等于75岁且不需要有人全天候陪同的概率为40%
【答案】BC
【解析】不妨设共有100名老人，则根据题意可作出如下表格：
所以如果从该养老院随机抽取一位老人，
抽到的老人年龄在75岁以下的概率为40%，故选项错误；
抽到的老人需要有人全天全天候陪同的概率为22%，故选项正确；
抽到的老人年龄在75岁以下且需要有人全天候陪同的概率为4%，故选项正确；
抽到的老人年龄大于等于75岁且不需要有人全天候陪同的概率为42%，故选项错误，
故选：.
13．（2023·全国·高一专题练习）在一个不透明的布袋中，红色、黑色、白色的玻璃球共有50个，除颜色外其他完全相同，小明通过多次摸球试验后发现其中摸到红色球，黑色球的频率稳定在30%和40%，则口袋中白色球的个数可能是__________个．
【答案】15
【解析】∵摸到红色球、黑色球的频率稳定在30%和40%，
∴摸到白球的频率为，
故口袋中白色球的个数可能是个．
故答案为：15
14．（2023·全国·高一专题练习）甲、乙两人向同一目标各射击一次，已知甲命中目标的概率为0.6，乙命中目标的概率为0.5，目标至少被命中1次的概率为________．
【答案】0.8/
【解析】记事件A：两次都未命中目标.
则
所以目标至少被命中1次的概率为.
故答案为：0.8
15．（2023·全国·高一专题练习）甲、乙两人独立地破解同一个谜题，破解出谜题的概率分别为，.则谜题被破解的概率为________.
【答案】
【解析】设“甲独立地破解谜题”为事件，“乙独立地破解谜题”为事件，
“谜题被破解”为事件，且事件，相互独立，
则.
故答案为：
16．（2023·高一课时练习）5支球队中，有3支亚洲队，2支非洲队，从中任意抽2队进行比赛，则两洲各有一队的概率是________．
【答案】/
【解析】设亚洲球队分别为，非洲球队分别为，
则所有情况为，共10种，
其中满足题意的共，共6种，
故概率为，
故答案为：.
17．（2023春·高一课时练习）现有7名学生，其中，，的数学成绩优秀，，的物理成绩优秀，，的化学成绩优秀.从中选出数学、物理、化学成绩优秀者各1名，组成一个小组代表学校参加竞赛.
（1）求被选中的概率；
（2）求和至多有一个被选中的概率.
【答案】（1）；（2）
【解析】（1）用表示从7人中选出数学、物理、化学成绩优秀者各1名，
则对应的样本空间
，
共有12个样本点，
记事件“被选中”，
则，
共有6个样本点，所以被选中的概率.
（2）记事件“，至多有一个被选中”，则其对立事件“，全被选中”
可得，共2个样本点，所以.
由对立事件的概率公式得.
18．（2023·高一课时练习）一枚均匀的硬币先后掷四次，求：
（1）恰有两枚“正面向上”的概率；
（2）至少有两枚“正面向上”的概率．
【答案】（1）；（2）
【解析】（1）设一枚硬币“正面向上”用表示，“反面向上”用表示，
四枚硬币投掷的结果可以用表示（其中仅取、）．
记事件恰有两枚“正面向上”，
枚硬币所掷出的结果包括：
、、、、、、、、
、、、、、、、，
共种．
其中事件包含的基本事件有：、、、、、
，共种．所以．
（2）记事件至少有两枚“正面向上”，
则事件所包含的基本事件有：、、、、、
、、、、、，共种，
所以，.
19．（2023·江苏·高一专题练习）甲、乙、丙三人进行羽毛球比赛，约定赛制如下:
累计负两场者被淘汰；比赛前抽签决定首先比赛的两人，另一人轮空:每场比赛的胜者与轮空者进行下一场比赛，负者下一场轮空，直至有一人被淘汰；当一人被淘汰后，剩余的两人继续比赛，直至其中一人被淘汰，另一人最终获胜，比赛结束.已知在每场比赛中，甲胜乙和甲胜丙的概率均为，乙胜丙的概率为，各场比赛的结果相互独立.经抽签，第一场比赛甲轮空.
（1）求前三场比赛结束后，丙被淘汰的概率；
（2）求只需四场比赛就决出冠军的概率；
（3）求甲最终获胜的概率.
【答案】（1）；（2）；（3）
【解析】（1）记事件A为甲胜乙，则，，
事件B为甲胜丙，则，，
事件C为乙胜丙，则，，
前三场比赛结束后，丙被淘汰的概率为
.
（2）只需四场比赛就决出冠军的概率为：
.
（3）由于甲胜乙和甲胜丙的概率均为，且乙胜丙和丙胜乙的概率也相等，均为，
第一场比赛甲当裁判，以后的比赛相对于甲，可视乙丙为同一人，
设甲胜为事件D，甲当裁判为事件E，
所以甲最终获胜的概率
.
20．（2023春·全国·高一专题练习）杭州2022年第19届亚运会（The 19th Asian Games Hangzhu 2022）将于2023年9月23日至10月8日举办．本届亚运会共设40个竞赛大项，包括31个奥运项目和9个非奥运项目．同时，在保持40个大项目不变的前提下，增设了电子竞技项目．与传统的淘汰赛不同，近年来一个新型的赛制“双败赛制”赢得了许多赛事的青睐．
传统的淘汰赛失败一场就丧失了冠军争夺的权利，而在双败赛制下，每人或者每个队伍只有失败了两场才会淘汰出局，因此更有容错率．假设最终进入到半决赛有四支队伍，淘汰赛制下会将他们四支队伍两两分组进行比赛，胜者进入到总决赛，总决赛的胜者即为最终的冠军．双败赛制下，两两分组，胜者进入到胜者组，败者进入到败者组，胜者组两个队伍对决的胜者将进入到总决赛，败者进入到败者组．之前进入到败者组的两个队伍对决的败者将直接淘汰，胜者将跟胜者组的败者对决，其中的胜者进入总决赛，最后总决赛的胜者即为冠军．双败赛制下会发现一个有意思的事情，在胜者组中的胜者只要输一场比赛即总决赛就无法拿到冠军，但是其它的队伍却有一次失败的机会，近年来从败者组杀上来拿到冠军的不在少数，因此很多人戏谑这个赛制对强者不公平，是否真的如此呢？
这里我们简单研究一下两个赛制．假设四支队伍分别为，其中对阵其他三个队伍获胜概率均为，另外三支队伍彼此之间对阵时获胜概率均为．最初分组时同组，同组．
（1）若，在淘汰赛赛制下，获得冠军的概率分别为多少？
（2）分别计算两种赛制下获得冠军的概率（用表示），并据此简单分析一下双败赛制下对队伍的影响，是否如很多人质疑的“对强者不公平”？
【答案】（1）；；（2）淘汰赛制获得冠军概率为，双败赛制获得冠军概率为；双败赛制下，会使得强者拿到冠军概率变大，弱者拿到冠军的概率变低，更加有利于筛选出“强者”，人们“对强者不公平”的质疑是不对的．
【解析】（1）记拿到冠军分别为事件淘汰赛赛制下，只需要连赢两场即可拿到冠军，因此，
对于想拿到冠军，首先得战胜，然后战胜中的胜者，
因此．
（2）记两种寒制下获得冠军的概率分别为，则.
而双败赛制下，获得冠军有三种可能性：（1）直接连赢三局；
（2）从胜者组掉入败者组然后杀回总决赛；（3）直接掉入败者组拿到冠军.
因此，，
.
则不论哪种赛制下，获得冠军的概率均小于，.
若，双败赛制下，队伍获得冠军的概率更大，
其他队伍获得冠军的概率会变小，
若，双败赛制下，以伍获得冠军的概率更小，
其他队伍获得冠军的概率会变大，
综上可知：双败赛制下，会使得强者拿到冠军概率变大，
弱者拿到冠军的概率变低，更加有利于筛选出“强者”，
人们“对强者不公平”的质疑是不对的．事件
表示
概率
A，B同时发生
P(A)P(B)
A，B都不发生
A，B恰有一个发生
A，B中至少有一个发生
A，B中至多有一个发生
投篮次数
投中两分球的次数
投中三分球的次数
100
55
18
卡片号码
1
2
3
4
5
6
7
8
9
10
取到的次数
13
8
5
7
6
13
18
10
11
9
汽车型号
Ⅰ
Ⅱ
Ⅲ
Ⅳ
Ⅴ
回访客户/人
250
100
200
700
350
满意率
0.5
0.3
0.6
0.3
0.2
需要陪同
不需要陪同
合计
75岁及以上
18
42
60
75岁以下
4
36
40
合计
22
78
100