
备考2024届高考数学一轮复习讲义第一章集合常用逻辑用语与不等式第1讲集合
展开1.集合的概念
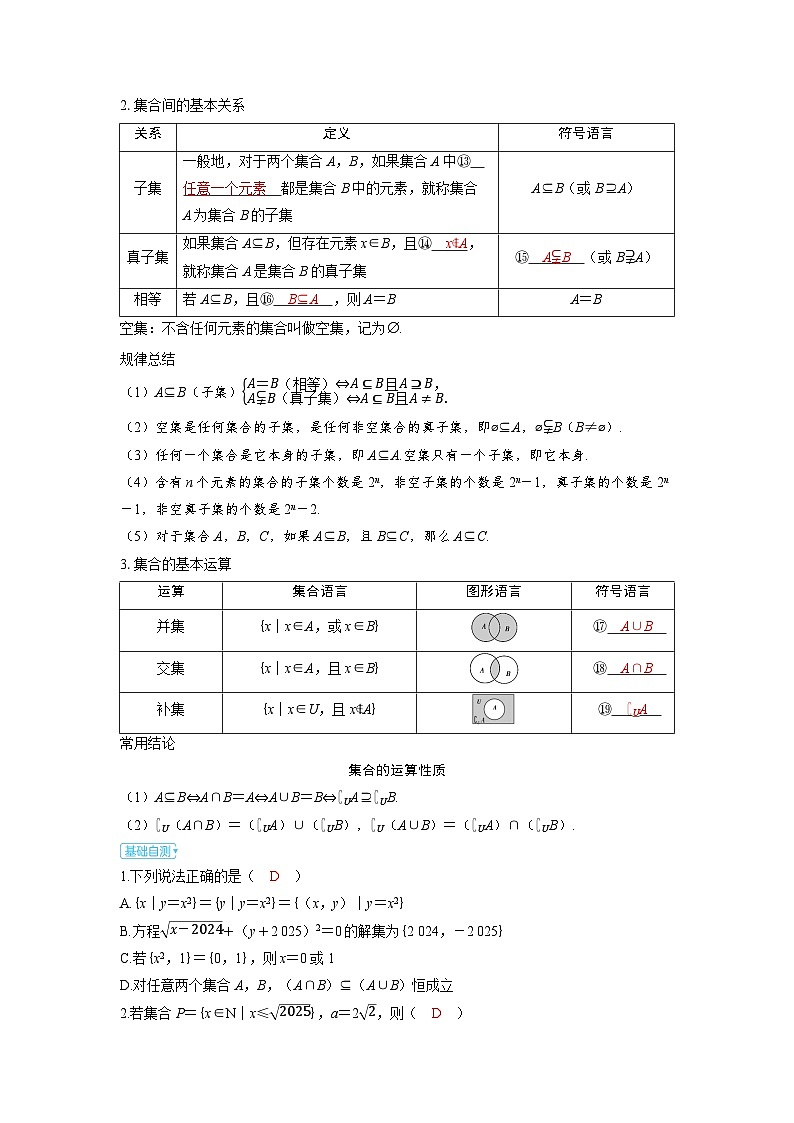
2.集合间的基本关系
空集:不含任何元素的集合叫做空集,记为∅.
规律总结
(1)A⊆B(子集)A=B(相等)⇔A⊆B且A⊇B,A⫋B(真子集)⇔A⊆B且A≠B.
(2)空集是任何集合的子集,是任何非空集合的真子集,即⌀⊆A,⌀⫋B(B≠⌀).
(3)任何一个集合是它本身的子集,即A⊆A.空集只有一个子集,即它本身.
(4)含有n个元素的集合的子集个数是2n,非空子集的个数是2n-1,真子集的个数是2n-1,非空真子集的个数是2n-2.
(5)对于集合A,B,C,如果A⊆B,且B⊆C,那么A⊆C.
3.集合的基本运算
常用结论
集合的运算性质
(1)A⊆B⇔A∩B=A⇔A∪B=B⇔∁UA⊇∁UB.
(2)∁U(A∩B)=(∁UA)∪(∁UB),∁U(A∪B)=(∁UA)∩(∁UB).
1.下列说法正确的是( D )
A.{x|y=x2}={y|y=x2}={(x,y)|y=x2}
B.方程x-2024+(y+2 025)2=0的解集为{2 024,-2 025}
C.若{x2,1}={0,1},则x=0或1
D.对任意两个集合A,B,(A∩B)⊆(A∪B)恒成立
2.若集合P={x∈N|x≤2025},a=22,则( D )
A.a∈PB.{a}∈PC.{a}⊆PD.a∉P
3.集合{a,b}的真子集的个数为 3 .
解析 解法一 集合{a,b}的真子集为⌀,{a},{b},有3个.
解法二 集合{a,b}有2个元素,则集合{a,b}的真子集的个数为22-1=3.
4.设a,b∈R,P={2,a},Q={-1,-b},若P=Q,则a-b= 1 .
解析 ∵P=Q,∴a=-1,-b=2,∴a-b=-1-(-2)=1.
5.已知集合U={1,2,3,4,5,6,7},A={2,4,5},B={1,3,5,7},则A∩(∁UB)= {2,4} ,(∁UA)∩(∁UB)= {6} .
解析 ∵∁UA={1,3,6,7},∁UB={2,4,6},∴A∩(∁UB)={2,4,5}∩{2,4,6}={2,4},(∁UA)∩(∁UB)={1,3,6,7}∩{2,4,6}={6}.
研透高考 明确方向
命题点1 集合的概念
例1 (1)[2022全国卷乙]设全集U={1,2,3,4,5},集合M满足∁UM={1,3},则( A )
A.2∈MB.3∈M
C.4∉MD.5∉M
解析 由题意知M={2,4,5},故选A.
(2)[全国卷Ⅲ]已知集合A={(x,y)|x,y∈N*,y≥x},B={(x,y)|x+y=8},则A∩B中元素的个数为( C )
A.2B.3
C.4D.6
解析 由题意得,A∩B={(1,7),(2,6),(3,5),(4,4)},所以A∩B中元素的个数为4,故选C.
方法技巧
1.解决集合含义问题的三个关键点:一是确定构成集合的元素;二是分析元素的限制条件;三是根据元素的特征(满足的条件)构造关系式解决相应问题.2.常见集合的含义
训练1 (1)[多选/2024黑龙江模拟]已知集合A={x|4ax2-4(a+2)x+9=0}中只有一个元素,则实数a的可能取值为( ABD )
A.0B.1C.2D.4
解析 当a=0时,-8x+9=0,解得x=98,所以A={98},符合题意;当a≠0时,由题意,得Δ=[4(a+2)]2-4×4a×9=0,解得a=1或a=4.故选ABD.
(2)[多选/2023江苏省镇江中学模拟]已知集合A={y|y=x2+2},集合B={(x,y)|y=x2+2},下列关系正确的是( AB )
A.(1,3)∈BB.(0,0)∉B
C.0∈AD.A=B
解析 ∵集合A={y|y≥2}=[2,+∞),集合B={(x,y)|y=x2+2}是由抛物线y=x2+2上的点组成的集合,∴AB正确,CD错误,故选AB.
(3)已知集合A={0,m,m2-5m+6},且2∈A,则实数m的值为 1或4 .
解析 因为A={0,m,m2-5m+6},2∈A,所以m=2或m2-5m+6=2.当m=2时,m2-5m+6=0,不满足集合中元素互异性,所以m=2不符合题意.当m2-5m+6=2时,m=1或m=4,
若m=1,A={0,1,2}符合题意;若m=4,A={0,4,2}符合题意.所以实数m的值为1或4.
命题点2 集合间的基本关系
例2 (1)[2023新高考卷Ⅱ]设集合A={0,-a},B={1,a-2,2a-2},若A⊆B,则a=( B )
A.2B.1C.23D.-1
解析 依题意,有a-2=0或2a-2=0.当a-2=0时,解得a=2,此时A={0,-2},B={1,0,2},不满足A⊆B;当2a-2=0时,解得a=1,此时A={0,-1},B={-1,0,1},满足A⊆B.所以a=1,故选B.
(2)[2024山西太原模拟]满足条件{1,2}⊆A⫋{1,2,3,4,5}的集合A的个数是( C )
A.5B.6C.7D.8
解析 解法一 因为集合{1,2}⊆A⫋{1,2,3,4,5},所以集合A可以是{1,2},{1,2,3},{1,2,4},{1,2,5},{1,2,3,4},{1,2,3,5},{1,2,4,5},共 7 个.故选C.
解法二 问题等价于求集合{3,4,5}的真子集的个数,则共有23-1=7个.故选C.
方法技巧
1.求集合的子集个数,常借助列举法和公式法求解.
2.根据两集合间的关系求参数,常根据集合间的关系转化为方程(组)或不等式(组)求解,求解时注意集合中元素的互异性和端点值能否取到.
注意 在涉及集合之间的关系时,若未指明集合非空,则要考虑空集的情况,如已知集合A、非空集合B满足A⊆B或A⫋B,则有A=⌀和A≠⌀两种情况.
训练2 (1)设集合P={y|y=x2+1},M={x|y=x2+1},则集合M与集合P的关系是( D )
A.M=PB.P∈M
C.M⫋PD.P⫋M
解析 ∵P={y|y=x2+1}={y|y≥1},M={x|y=x2+1}=R,∴P⫋M.故选D.
(2)已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B⊆A,则实数m的取值范围为 (-∞,3] .
解析 因为B⊆A,所以分以下两种情况:
①若B=∅,则2m-1<m+1,此时m<2;
②若B≠∅,则2m-1≥m+1,m+1≥-2,2m-1≤5,解得2≤m≤3.
由①②可得,符合题意的实数m的取值范围为(-∞,3].
命题点3 集合的基本运算
角度1 集合的交、并、补运算
例3 (1)[2023新高考卷Ⅰ]已知集合M={-2,-1,0,1,2},N={x|x2-x-6≥0},则M∩N=( C )
A.{-2,-1,0,1}B.{0,1,2}
C.{-2}D.{2}
解析 解法一因为N={x|x2-x-6≥0}={x|x≥3或x≤-2},所以M∩N={-2},故选C.
解法二 因为1∉N,所以1∉M∩N,排除A,B;因为2∉N,所以2∉M∩N,排除D.故选C.
(2)[2023全国卷甲]设全集U=Z,集合M={x|x=3k+1,k∈Z},N={x|x=3k+2,k∈Z},则∁U(M∪N)=( A )
A.{x|x=3k,k∈Z}B.{x|x=3k-1,k∈Z}
C.{x|x=3k-2,k∈Z}D.∅
解析 解法一 M={…,-2,1,4,7,10,…},N={…,-1,2,5,8,11,…},所以M∪N={…,-2,-1,1,2,4,5,7,8,10,11,…},所以∁U(M∪N)={…,-3,0,3,6,9,…},其元素都是3的倍数,即∁U(M∪N)={x|x=3k,k∈Z},故选A.
解法二 集合M∪N表示被3除余1或2的整数集,则它在整数集中的补集是恰好能被3整除的整数集,故选A.
角度2 已知集合运算结果求参数
例4 (1)[全国卷Ⅰ]设集合A={x|x2-4≤0},B={x|2x+a≤0},且A∩B={x|-2≤x≤1},则a=( B )
A.-4B.-2C.2D.4
解析 易知A={x|-2≤x≤2},B={x|x≤-a2},因为A∩B={x|-2≤x≤1},所以-a2=1,解得a=-2.故选B.
(2)已知集合A={x|y=ln(1-x2)},B={x|x≤a},若(∁RA)∪B=R,则实数a的取值范围为( B )
A.(1,+∞)B.[1,+∞)
C.(-∞,1)D.(-∞,1]
解析 由题可知A={x|y=ln(1-x2)}={x|-1<x<1},∁RA={x|x≤-1或x≥1},所以由(∁RA)∪B=R,B={x|x≤a},得a≥1.
方法技巧
1.处理集合的交、并、补运算时,一是要明确集合中的元素是什么,二是要能够化简集合,得出元素满足的最简条件.
2.对于集合的交、并、补运算,如果集合中的元素是离散的,可借助Venn图求解;如果集合中的元素是连续的,可借助数轴求解,此时要注意端点的情况.
训练3 (1)[2023全国卷乙]设集合U=R,集合M={x|x<1},N={x|-1<x<2},则{x|x≥2}=( A )
A.∁U(M∪N)B.N∪∁UM
C.∁U(M∩N)D.M∪∁UN
解析 由题意知M∪N={x|x<2},所以∁U(M∪N)={x|x≥2},故选A.
(2)[2023江西省联考]已知集合A={(x,y)|(x-1)2+y2=1},B={(x,y)|kx-y-2<0}.若A∩B=A,则实数k的取值范围是( A )
A.(-∞,34)B.(34,3)
C.(34,+∞)D.(-∞,34]
解析 因为A∩B=A,所以A⊆B,则圆(x-1)2+y2=1在直线y=kx-2的上方,则k×1-2<0,|k×1-0-2|k2+(-1)2>1,解得k<34.
命题点4 集合中的计数问题
例5 [全国卷Ⅲ]《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为( C )
A.0.5B.0.6C.0.7D.0.8
解析 解法一 由题意得,阅读过《西游记》的学生人数为 90-80+60=70,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为70÷100=0.7.故选C.
解法二 用Venn图表示调查的100位学生中阅读过《西游记》和《红楼梦》的人数之间的关系,如图,
易知调查的100位学生中阅读过《西游记》的学生人数为70,所以该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为70100=0.7.故选C.
方法技巧
集合中元素的个数问题的求解策略
关于集合中元素的个数问题,常借助Venn图或用公式card(A∪B)=card(A)+
card(B)- card(A∩B),card(A∪B∪C)=card(A)+card(B)+card(C)-
card(A∩B)-card(A∩C)-card(B∩C)+card(A∩B∩C)(card(A)表示有限集合A中元素的个数)求解.
训练4 向50名学生调查对A,B两种观点的态度,结果如下:赞成观点A的学生人数是全体人数的35,其余的不赞成;赞成观点B的学生人数比赞成观点A的多3人,其余的不赞成;另外,对观点A,B都不赞成的学生人数比对观点A,B都赞成的学生人数的13多1人,则对观点A,B都赞成的学生有 21 人.
解析 赞成观点A的学生人数为50×35=30,赞成观点B的学生人数为30+3=33.如图,记50名学生组成的集合为U,赞成观点A的学生全体为集合A,赞成观点B的学生全体为集合B.设对观点A,B都赞成的学生人数为x,则对观点A,B都不赞成的学生人数为x3+1,赞成观点A或赞成观点B的学生人数为30+33-x.依题意30+33-x+x3+1=50,解得x=21.故对观点A,B都赞成的学生有21人.
命题点5 集合的新定义问题
例6 (1)[2024上海市晋元高级中学模拟]已知集合M={1,2,3,4,5,6},集合A⊆M,定义M(A)为A中元素的最小值,当A取遍M的所有非空子集时,对应的
M(A)的和记为S,则S= 120 .
解析 由M={1,2,3,4,5,6}得,M的非空子集A共有26-1个,其中最小值为1的有25个,最小值为2的有24个,最小值为3的有23个,最小值为4的有22个,最小值为5的有21个,最小值为6的有20个,故S=25×1+24×2+23×3+22×4+2×5+1×6=120.
(2)若一个集合是另一个集合的子集,则称这两个集合构成“全食”;若两个集合有公共元素但不互为对方的子集,则称两个集合构成“偏食”.已知集合A={x|-t<x<t,t>0}和集合B={x|x2-x-2<0},若集合A,B构成“偏食”,则实数t的取值范围为 (1,2) .
解析 由题意,可知集合A={x|-t<x<t,t>0},集合B={x|-1<x<2},因为集合A,B构成“偏食”,所以t>0,-t<-1
解决集合新定义问题的关键
紧扣新定义,分析新定义的特点,把新定义所叙述的问题的本质弄清楚,结合题目所给定义和要求进行恰当转化,切忌同已有概念或定义混淆.
训练5 [多选/2023山东省淄博一中月考]在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为[k],即[k]={5n+k|n∈Z}(k=0,1,2,3,4),给出如下四个结论,正确结论为( ACD )
A.2 023∈[3]
B.-2∈[2]
C.Z=[0]∪[1]∪[2]∪[3]∪[4]
D.整数a,b属于同一“类”的充要条件是a-b∈[0]
解析 由2 023÷5=404……3,得2 023∈[3],故A正确;-2=5×(-1)+3,所以
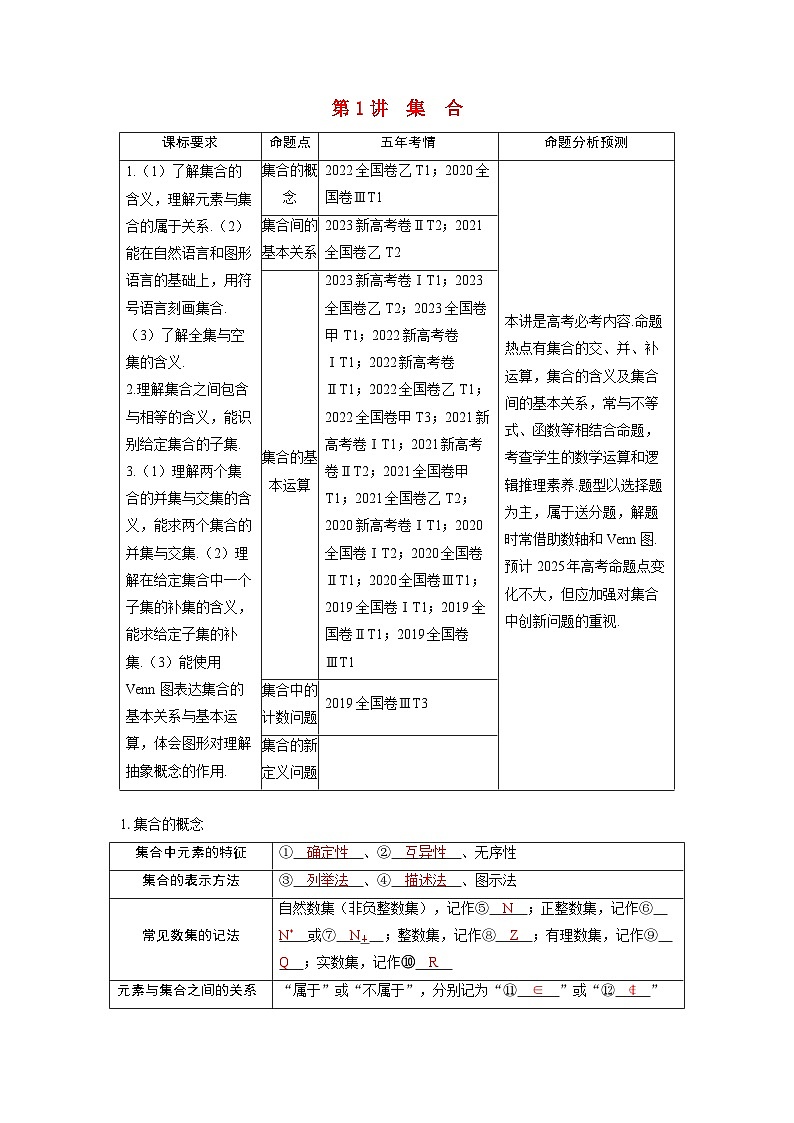
-2∈[3],故B错误;因为整数集中的被5除的数可以且只可以分成五类,所以Z=[0]∪[1]∪[2]∪[3]∪[4],故C正确;因为整数a,b属于同一“类”,所以整数a,b被5除的余数相同,从而a-b被5除的余数为0,反之也成立,故整数a,b属于同一“类”的充要条件是a-b∈[0],故D正确.故选ACD.课标要求
命题点
五年考情
命题分析预测
1.(1)了解集合的含义,理解元素与集合的属于关系.(2)能在自然语言和图形语言的基础上,用符号语言刻画集合.(3)了解全集与空集的含义.
2.理解集合之间包含与相等的含义,能识别给定集合的子集.
3.(1)理解两个集合的并集与交集的含义,能求两个集合的并集与交集.(2)理解在给定集合中一个子集的补集的含义,能求给定子集的补集.(3)能使用Venn图表达集合的基本关系与基本运算,体会图形对理解抽象概念的作用.
集合的概念
2022全国卷乙T1;2020全国卷ⅢT1
本讲是高考必考内容.命题热点有集合的交、并、补运算,集合的含义及集合间的基本关系,常与不等式、函数等相结合命题,考查学生的数学运算和逻辑推理素养.题型以选择题为主,属于送分题,解题时常借助数轴和Venn图.预计2025年高考命题点变化不大,但应加强对集合中创新问题的重视.
集合间的基本关系
2023新高考卷ⅡT2;2021全国卷乙T2
集合的基本运算
2023新高考卷ⅠT1;2023全国卷乙T2;2023全国卷甲T1;2022新高考卷ⅠT1;2022新高考卷ⅡT1;2022全国卷乙T1;2022全国卷甲T3;2021新高考卷ⅠT1;2021新高考卷ⅡT2;2021全国卷甲T1;2021全国卷乙T2;2020新高考卷ⅠT1;2020全国卷ⅠT2;2020全国卷ⅡT1;2020全国卷ⅢT1;2019全国卷ⅠT1;2019全国卷ⅡT1;2019全国卷ⅢT1
集合中的计数问题
2019全国卷ⅢT3
集合的新定义问题
集合中元素的特征
① 确定性 、② 互异性 、无序性
集合的表示方法
③ 列举法 、④ 描述法 、图示法
常见数集的记法
自然数集(非负整数集),记作⑤ N ;正整数集,记作⑥ N* 或⑦ N+ ;整数集,记作⑧ Z ;有理数集,记作⑨ Q ;实数集,记作⑩ R
元素与集合之间的关系
“属于”或“不属于”,分别记为“⑪ ∈ ”或“⑫ ∉ ”
关系
定义
符号语言
子集
一般地,对于两个集合A,B,如果集合A中⑬ 任意一个元素 都是集合B中的元素,就称集合A为集合B的子集
A⊆B(或B⊇A)
真子集
如果集合A⊆B,但存在元素x∈B,且⑭ x∉A,就称集合A是集合B的真子集
⑮ A⫋B (或B⫌A)
相等
若A⊆B,且⑯ B⊆A ,则A=B
A=B
运算
集合语言
图形语言
符号语言
并集
{x|x∈A,或x∈B}
⑰ A∪B
交集
{x|x∈A,且x∈B}
⑱ A∩B
补集
{x|x∈U,且x∉A}
⑲ ∁UA
集合
{x|f(x)=0}
{x|f(x)>0}
{x|y=f(x)}
{y|y=f(x)}
{(x,y)|y=
f(x)}
代表元素
方程f(x)=
0的根
不等式f(x)>0的解
函数y=f(x)的自变量的取值
函数y=f(x)的函数值
函数y=f(x)图象上的点
备考2024届高考数学一轮复习讲义第一章集合常用逻辑用语与不等式第3讲等式性质与不等式性质: 这是一份备考2024届高考数学一轮复习讲义第一章集合常用逻辑用语与不等式第3讲等式性质与不等式性质,共6页。
备考2024届高考数学一轮复习讲义第一章集合常用逻辑用语与不等式第2讲常用逻辑用语: 这是一份备考2024届高考数学一轮复习讲义第一章集合常用逻辑用语与不等式第2讲常用逻辑用语,共7页。
备考2024届高考数学一轮复习讲义第一章集合常用逻辑用语与不等式第4讲基本不等式: 这是一份备考2024届高考数学一轮复习讲义第一章集合常用逻辑用语与不等式第4讲基本不等式,共10页。












