备考2024届高考数学一轮复习讲义第二章函数第5讲对数与对数函数

这是一份备考2024届高考数学一轮复习讲义第二章函数第5讲对数与对数函数，共9页。学案主要包含了四象限.等内容，欢迎下载使用。
（1）对数的概念
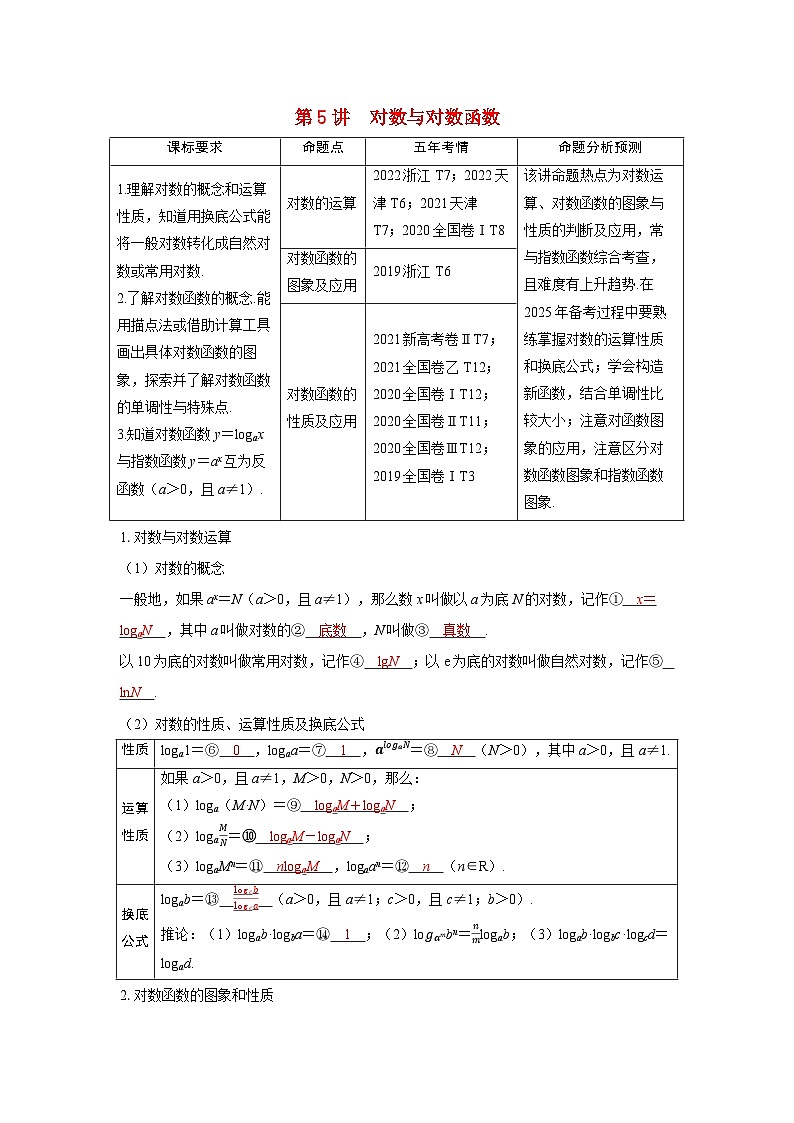
一般地，如果ax＝N（a＞0，且a≠1），那么数x叫做以a为底N的对数，记作① x＝lgaN ，其中a叫做对数的② 底数 ，N叫做③ 真数 .
以10为底的对数叫做常用对数，记作④ lgN ；以e为底的对数叫做自然对数，记作⑤ lnN .
（2）对数的性质、运算性质及换底公式
2.对数函数的图象和性质
规律总结
1.对数函数y＝lgax（a＞0，且a≠1）的图象过定点（1，0），且过点（a，1），（1a，
－1），函数图象只在第一、四象限.
2.如图，作直线y＝1，则该直线与四个函数图象交点的横坐标为相应的底数，故0＜c＜d＜1＜a＜b.由此我们可得到以下规律：在第一象限内从左到右对数函数的底数逐渐增大.
注意 当对数函数的底数a的大小不确定时，需分a＞1和0＜a＜1两种情况进行讨论.
3.反函数
指数函数y＝ax（a＞0，且a≠1）与对数函数y＝lgax（a＞0，且a≠1）互为反函数，它们的图象关于直线⑳ y＝x 对称（如图所示）.反函数的定义域、值域分别是原函数的值域、定义域，互为反函数的两个函数具有相同的单调性、奇偶性.
1.[全国卷Ⅰ]设alg34＝2，则4－a＝（ B ）
A.116B.19C.18D.16
解析 解法一 因为alg34＝2，所以lg34a＝2，则有4a＝32＝9，所以4－a＝14a＝19，故选B.
解法二 因为alg34＝2，所以a＝2lg34＝lg39lg34＝lg49，所以4a＝9，所以4－a＝14a＝19，故选B.
2.[多选]以下说法正确的是（ CD ）
A.若MN＞0，则lga（MN）＝lgaM＋lgaN
B.对数函数y＝lgax（a＞0且a≠1）在（0，＋∞）上是增函数
C.函数y＝ln 1+x1－x与y＝ln（1＋x）－ln（1－x）的定义域相同
D.对数函数y＝lgax（a＞0且a≠1）的图象过定点（1，0）且过点（a，1）,（1a，
－1），函数图象只在第一、四象限
3.lg 25＋lg 2·lg 50＋（lg 2）2＝ 2 .
4.若lga34＜1（a＞0，且a≠1），则实数a的取值范围是 （0，34）∪（1，＋∞） .
5.设lga2＝m，lga3＝n，则a2m＋n的值为 12 .
6.[2023北京高考]已知函数f（x）＝4x＋lg2x，则f（12）＝ 1 .
解析 因为f（x）＝4x＋lg2x，所以f（12）＝412＋lg212＝2＋lg22－1＝2－1＝1.
研透高考 明确方向
命题点1 对数的运算
例1 （1）[2022天津高考]化简（2lg43＋lg83）（lg32＋lg92）的值为（ B ）
A.1B.2C.4D.6
解析 （2lg43＋lg83）（lg32＋lg92）＝（2lg223＋lg233）×（lg32＋lg322）＝（lg23＋13lg23）（lg32＋12lg32）＝43×lg23×32×lg32＝2，故选B.
（2）[2022浙江高考]已知2a＝5，lg83＝b，则4a－3b＝（ C ）
A.25B.5C.259D.53
解析 由2a＝5得a＝lg25.又b＝lg83＝lg23lg28＝13lg23，所以a－3b＝lg25－lg23＝lg253＝lg453lg42＝2lg453＝lg4259，所以4a－3b＝4lg4259＝259，故选C.
方法技巧
对数运算的一般思路
（1）转化：①利用ab＝N⇔b＝lgaN（a＞0且a≠1）对题目条件进行转化；②利用换底公式化为同底数的对数运算.
（2）利用恒等式：lga1＝0，lgaa＝1，lgaaN＝N，algaM＝M.
（3）拆分：将真数化为积、商或底数的指数幂形式，正用对数的运算性质化简.
（4）合并：将对数式化为同底数对数的和、差、倍数的运算，然后逆用对数的运算性质，转化为同底数对数的真数的积、商、幂的运算.
训练1 （1）[2024江苏省如皋市教学质量调研]我们知道，任何一个正实数N可以表示成N＝a×10n（1≤a＜10，n∈Z），此时lg N＝n＋lg a（0≤lg a＜1）.当n＞0时，N是n＋1位数，则41 000是（ C ）位数.（lg 2≈0.301 0）
A.601B.602C.603D.604
解析 由lg41 000＝lg22 000＝2 000lg 2≈2 000×0.301 0＝602＝602＋lg 1，得n＝602，所以41 000是603位数.故选C.
（2）[2024山东泰安第二中学模拟]（2＋1027）－23＋2lg32－lg349－5lg259＝ －716 .
解析 原式＝[（43）3]－23＋lg34－lg349－5lg53＝（43）－2＋lg39－3 ＝916＋2－3＝－716.
命题点2 对数函数的图象及应用
例2 （1）[浙江高考]在同一直角坐标系中，函数y＝1ax，y＝lga（x＋12）（a＞0，且a≠1）的图象可能是（ D ）
AB
CD
解析 若0＜a＜1，则函数y＝1ax是增函数，y＝lga（x＋12）是减函数且其图象过点（12，0），结合选项可知，选项D可能成立；若a＞1，则y＝1ax是减函数，而y＝lga（x＋12）是增函数且其图象过点（12，0），结合选项可知，没有符合的图象.故选D.
（2）已知当0＜x≤14时，有x＜lgax，则实数a的取值范围为 （116，1） .
解析 若x＜lgax在x∈（0，14]时成立，则0＜a＜1，且y＝x的图象在y＝lgax图象的下方，作出y＝x，y＝lgax的图象如图所示.由图象知14＜lga14，所以0